Plantilla:Rectas y puntos notables en un triángulo
De Wikipedia
| Revisión de 09:50 19 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:51 19 jul 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| |sinopsis=Medianas y baricentro de un triángulo. Propiedad del baricentro. | |sinopsis=Medianas y baricentro de un triángulo. Propiedad del baricentro. | ||
| }} | }} | ||
| - | {{Video_enlace | + | {{Video_enlace_8cifras |
| |titulo1=Construcción del baricentro | |titulo1=Construcción del baricentro | ||
| |duracion=3´11" | |duracion=3´11" | ||
| Línea 32: | Línea 32: | ||
| |sinopsis=Alturas y ortocentro de un triángulo según sea rectángulo, acutángulo u obtusángulo. | |sinopsis=Alturas y ortocentro de un triángulo según sea rectángulo, acutángulo u obtusángulo. | ||
| }} | }} | ||
| - | {{Video_enlace | + | {{Video_enlace_8cifras |
| |titulo1=Construcción del ortocentro | |titulo1=Construcción del ortocentro | ||
| |duracion=2´48" | |duracion=2´48" | ||
| Línea 48: | Línea 48: | ||
| :Las tres mediatrices siempre se cortan en un punto llamado '''circuncentro''', que es el centro de la circunferencia circunscrita al triángulo, que pasa por los tres vértices del triángulo. | :Las tres mediatrices siempre se cortan en un punto llamado '''circuncentro''', que es el centro de la circunferencia circunscrita al triángulo, que pasa por los tres vértices del triángulo. | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace | + | {{Video_enlace_8cifras |
| |titulo1=Construcción del circuncentro | |titulo1=Construcción del circuncentro | ||
| |duracion=3´12" | |duracion=3´12" | ||
| Línea 64: | Línea 64: | ||
| :Las tres '''bisectrices''' de un triángulo cualquiera se cortan en un punto llamado '''incentro''', que es el centro de la circunferencia inscrita al triángulo, que es tangente a los tres lados del triángulo. | :Las tres '''bisectrices''' de un triángulo cualquiera se cortan en un punto llamado '''incentro''', que es el centro de la circunferencia inscrita al triángulo, que es tangente a los tres lados del triángulo. | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace | + | {{Video_enlace_8cifras |
| |titulo1=Construcción del incentro | |titulo1=Construcción del incentro | ||
| |duracion=2´43" | |duracion=2´43" | ||
| Línea 79: | Línea 79: | ||
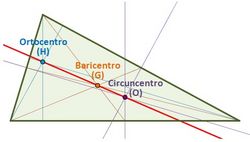
| :La recta de Euler de un triángulo es aquella recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo | :La recta de Euler de un triángulo es aquella recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace | + | {{Video_enlace_8cifras |
| |titulo1=Recta de Euler | |titulo1=Recta de Euler | ||
| |duracion=2´13" | |duracion=2´13" | ||
Revisión de 09:51 19 jul 2017
- Medianas y baricentro
Medianas y baricentro de un triángulo. Propiedad del baricentro. Construcción de las medianas y del baricentro de un triángulo. En esta escena podrás ver e interactuar con un triángulo y ver su baricentro y sus medianas. |
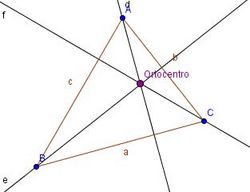
- Alturas y ortocentro
Alturas y ortocentro de un triángulo según sea rectángulo, acutángulo u obtusángulo. Construcción de las alturas y del ortocentro de un triángulo. En esta escena podrás ver e interactuar con un triángulo y ver su ortocentro y sus alturas. |
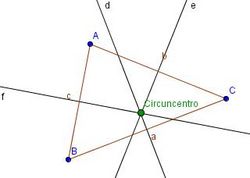
- Mediatrices y circuncentro
Construcción de las mediatrices y del circuncentro de un triángulo. En esta escena podrás ver e interactuar con un triángulo y ver su circuncentro y sus mediatrices. |
- Bisectrices e incentro
Construcción de las bisectrices y del incentro de un triángulo. En esta escena podrás ver e interactuar con un triángulo y ver su incentro y sus bisectrices. |
- Recta de Euler
Construcción de la recta de Euler. En esta escena podrás ver e interactuar con un triángulo y ver la recta de Euler. |
Actividades en las que podrás aprender cuáles son los puntos y rectas notables de un triángulo.
En este video vamos a estudiar las rectas y puntos notables de un triángulo:
- Rectas: bisectriz, mediana, mediatriz y altura.
- Puntos: incentro, baricentro, circuncentro y ortocentro.