Potencias de fracciones (2º ESO)
De Wikipedia
| Revisión de 09:11 3 sep 2017 Coordinador (Discusión | contribuciones) (→Potencias de base 10) ← Ir a diferencia anterior |
Revisión de 09:35 3 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| (Pág. 78) | (Pág. 78) | ||
| {{p}} | {{p}} | ||
| - | ==Potencias de fracciones== | + | ==Potencias de exponente negativo== |
| - | ===Potencias de exponente negativo=== | + | |
| {{Def potencia exponente entero}} | {{Def potencia exponente entero}} | ||
| {{p}} | {{p}} | ||
| Línea 16: | Línea 15: | ||
| {{p}} | {{p}} | ||
| - | ===Propiedades de las potencias de números racionales=== | + | ==Propiedades de las potencias de números racionales== |
| Las potencias con números racionales cumplen las mismas propiedades que con números enteros. | Las potencias con números racionales cumplen las mismas propiedades que con números enteros. | ||
| Línea 44: | Línea 43: | ||
| }} | }} | ||
| - | ===Ejercicios propuestos=== | + | ==Ejercicios propuestos== |
| {{ejercicio | {{ejercicio | ||
| |titulo=Ejercicios propuestos: ''Potencias de fracciones'' | |titulo=Ejercicios propuestos: ''Potencias de fracciones'' | ||
| Línea 55: | Línea 54: | ||
| |sol= | |sol= | ||
| }} | }} | ||
| - | |||
| - | (Pág. 81) | ||
| - | ==Potencias de base 10== | ||
| - | {{Potencias de 10}} | ||
| - | {{Videos: Potencias de 10}} | ||
| - | {{p}} | ||
| - | ===Operaciones con potencias de base 10=== | ||
| - | {{Productos y cocientes con potencias de 10}} | ||
| - | {{p}} | ||
| - | |||
| - | ===Descomposición polinómica de un número=== | ||
| - | {{Definición: Descomposición polinómica número}} | ||
| - | {{p}} | ||
| - | Ya conoces del curso pasado la descomposición polinómica de un número natural: | ||
| - | |||
| - | Ver: [[Potencias de base 10 (1º ESO)#Descomposición polinómica de un número|Descomposición polinómica de un número natural]] | ||
| - | |||
| - | A continuación veremos como se descompone un número decimal: | ||
| - | {{p}} | ||
| - | |||
| - | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | ||
| - | Para descomponer polinómicamente un número decimal procederemos de la siguiente manera: | ||
| - | *La parte entera del número se descompone como se hace con los números naturales, utilizando potencias de exponente positivo, teniendo en cuenta las equivalencias: | ||
| - | |||
| - | <center><math>10^0=1 \, ; \ 10^1=10 \, ; \ 10^2=100 \, ; \ 10^3=1000 \, ; \ \cdots</math></center> | ||
| - | |||
| - | *La parte decimal del número se descompone de forma análoga pero utilizando potencias de exponente negativo, teniendo en cuenta las siguientes equivalencias: | ||
| - | |||
| - | <center><math>10^{-1}=0.1 \, ; \ 10^{-2}=0.01 \, ; \ 10^{-3}=0.001 \, ; \ \cdots</math></center> | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplo|contenido=Vamos a obtener la descomposición polinómica del número 5034.652: | ||
| - | |||
| - | <math>5034.652 = 5000 + 30 + 4 + 0.6 + 0.05 + 0.002 =\;</math> | ||
| - | :::<math>= 5 \cdot 10^3 + 3 \cdot 10^1 + 4 \cdot 10^0 + 6 \cdot 10^{-1} + 5 \cdot 10^{-2} + 2 \cdot 10^{-3} | ||
| - | </math>}} | ||
| - | {{p}} | ||
| - | |||
| - | ===Notación científica=== | ||
| - | {{Definición: Notacion cientifica}} | ||
| - | {{p}} | ||
| - | {{Videotutoriales|titulo=Notación científica|enunciado= | ||
| - | {{Video_enlace_tutomate | ||
| - | |titulo1=Tutorial 1 | ||
| - | |duracion=7'37" | ||
| - | |sinopsis=Números en notación científica. Ejemplos. | ||
| - | |url1=https://www.youtube.com/watch?v=B-ZJywpOLzw&list=PLWRbPOo5oaTcOZhRaF3-DuT9bjIDrP8ZB&index=5 | ||
| - | }} | ||
| - | {{Video_enlace | ||
| - | |titulo1=Tutorial 2 | ||
| - | |duracion=5'19" | ||
| - | |sinopsis=Potencias de 10 y notación científica. Ejemplos. | ||
| - | |url1=https://www.youtube.com/watch?v=rssQ5Vg3nDk | ||
| - | }} | ||
| - | ---- | ||
| - | {{Video_enlace | ||
| - | |titulo1=Ejercicio 1 | ||
| - | |duracion=4'22" | ||
| - | |sinopsis=Escribe en notación científica: | ||
| - | |||
| - | a) 407 000 000 000 000 | ||
| - | |||
| - | b) 24 000 | ||
| - | |||
| - | c) 0.000 000 078 | ||
| - | |||
| - | |url1=https://www.youtube.com/watch?v=bg_4G32yCnM | ||
| - | }} | ||
| - | {{Video_enlace | ||
| - | |titulo1=Ejercicio 2 | ||
| - | |duracion=6'32" | ||
| - | |sinopsis=Escribe en notación científica: | ||
| - | |||
| - | a) 5 000 000 000{{b4}}{{b4}}b) 27 000{{b4}}{{b4}}c) 900{{b4}}{{b4}}d) 129 000 | ||
| - | |||
| - | e) 0.000 000 025{{b4}}{{b4}}f) 0.000 678{{b4}}{{b4}}g) 0.000 000 000 000 853 | ||
| - | |url1=https://www.youtube.com/watch?v=EMYTxbpXnJI | ||
| - | }} | ||
| - | }} | ||
| - | {{AI_descartes|titulo1=Ejemplos de números en notación científica | ||
| - | |descripcion=En la siguiente escena, genera distintos números, pulsando el botón inferior. | ||
| - | |||
| - | Anótalos en tu cuaderno, explicando qué condiciones cumple para que esté en notación científica. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/notacion/notacion_cientifica_1.html | ||
| - | width=700 | ||
| - | height=450 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/notacion/notacion_cientifica_1.html | ||
| - | }} | ||
| - | {{AI_descartes|titulo1=Significado del exponente en la notación científica | ||
| - | |descripcion=Consulta la ayuda de la escena y contesta. | ||
| - | |||
| - | Modifica los valores de las cifras y del exponente y observa qué sucede con la coma en los siguientes casos: | ||
| - | |||
| - | *Si el exponente es cero | ||
| - | *Si el exponente es negativo | ||
| - | *Si el exponente es positivo | ||
| - | |||
| - | Anota en tu cuaderno las conclusiones a las que hayas llegado. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/notacion/notacion_cientifica_3.html | ||
| - | width=700 | ||
| - | height=350 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/descartes/1y2_eso/notacion/notacion_cientifica_3.html | ||
| - | }} | ||
| - | {{AI_cidead | ||
| - | |titulo1=Notación científica | ||
| - | |descripcion=Actividades para aprender a manejar la notación científica. | ||
| - | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena1/2quincena1_contenidos_3b.htm | ||
| - | }} | ||
| - | |||
| - | ===Ejercicios propuestos=== | ||
| - | {{ejercicio | ||
| - | |titulo=Ejercicios propuestos: ''Potencias de fracciones'' | ||
| - | |cuerpo= | ||
| - | (Pág. 81) | ||
| - | |||
| - | [[Imagen:red_star.png|12px]] 15, 16, 17, 18 | ||
| - | |sol= | ||
| - | }} | ||
| - | |||
| [[Categoría: Ejercicios de Matemáticas|Números]] | [[Categoría: Ejercicios de Matemáticas|Números]] | ||
Revisión de 09:35 3 sep 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 78)
Potencias de exponente negativo
Se define la potencia de exponente negativo como:

Como consecuencia:
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos.
 . Ejemplos.
. Ejemplos.
Exponentes negativos. Ejemplos.
Razonando sobre el por qué de la definición de los exponentes negativos.
Simplifica:
- a)
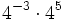
- b)
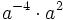
- c)
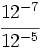
- d)
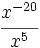
Simplifica:
- a)
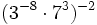
- b)
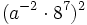
- c)
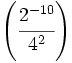
Halla el valor de:
11) 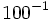 ; 12)
; 12) 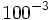 ; 13)
; 13) 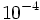 ; 14)
; 14) 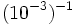
15) 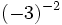 ; 16)
; 16) 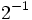 ; 17)
; 17) 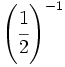 ; 18)
; 18) 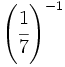 ; 19)
; 19) 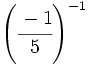
Potencias de exponente negativo.
Actividades sobre potencias de exponente negativo.
Calcula las siguientes potencias y comprueba los resultados en la escena siguiente:
a) 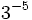 b)
b) 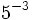 c)
c) 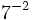 d)
d) 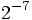
Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba.
Potencias de exponente negativo.
Multiplica y divide potencias (exponentes enteros).
Potencias de productos y cocientes (exponentes enteros)
Potencias de exponentes enteros.
Pulsa el botón "EJERCICIO" y lee atentamente el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien.
Ejercicios de autoevaluación sobre potencias de exponente negativo.
Propiedades de las potencias de números racionales
Las potencias con números racionales cumplen las mismas propiedades que con números enteros.
Ver: Propiedades de las potencias de números enteros
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
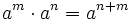
- 2. Cociente de potencias de la misma base:
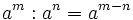
- 3. Potencia de un producto:
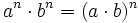
- 4. Potencia de un cociente:
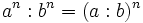
- 5. Potencia de otra potencia:
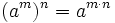
Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa.
Simplifica:
- a)
![\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3](/wikipedia/images/math/f/e/c/fec21991837955f9b9d945d4600cba18.png)
- b)
![\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2}](/wikipedia/images/math/e/5/1/e5178ed20376c4ef7f07ca88d5d43975.png)
Simplifica 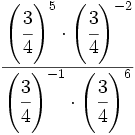
Simplifica: ![\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2](/wikipedia/images/math/6/9/1/6911b07dbbc54e802f87f7498ab77b09.png)
Ejemplos: Potencias de fracciones
Calcula simplificando previamente:
a) 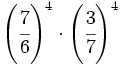 b)
b) 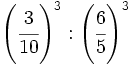 c)
c) 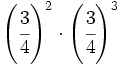
d) 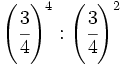 e)
e) 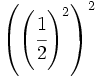 f)
f) 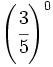
a)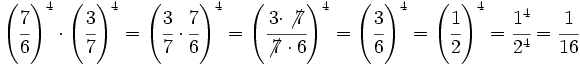
b)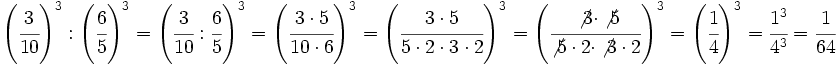
c)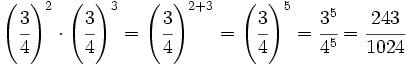
d)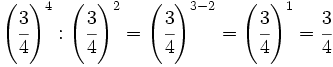
e) 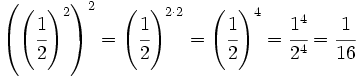
f)
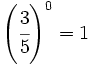
Ejercicios propuestos
|
Ejercicios propuestos: Potencias de fracciones |