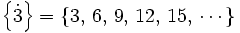Relación de divisibilidad (2º ESO)
De Wikipedia
| Revisión de 05:49 21 sep 2017 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) ← Ir a diferencia anterior |
Revisión de 18:26 19 oct 2017 Coordinador (Discusión | contribuciones) (→Múliplo y divisor) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| {{Relacion de divisibilidad}} | {{Relacion de divisibilidad}} | ||
| {{p}} | {{p}} | ||
| - | ==Múliplo y divisor== | + | ==Múliplos y divisores== |
| {{Def Multiplo y divisor}} | {{Def Multiplo y divisor}} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Múltiplos de un número== | ==Múltiplos de un número== | ||
| {{Cálculo de los múltiplos de un número}} | {{Cálculo de los múltiplos de un número}} | ||
Revisión de 18:26 19 oct 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Relación de divisibilidad
Dos números enteros  y
y  (
(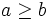 ) , están emparentados por la relación de divisibilidad cuando la división
) , están emparentados por la relación de divisibilidad cuando la división 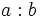 es exacta.
es exacta.
- Un listón de 60 cm se puede partir, exactamente, en trozos de 15 cm, porque la división 60:15 es exacta (cociente=4; resto=0). Por tanto, 60 y 15 están emparentados por la relación de divisibilidad.
- Un listón de 60 cm no se puede partir, exactamente, en trozos de 25 cm, porque la división 60:25 no es exacta (cociente=2; resto=10). Así, 60 y 25 no están emparentados por la relación de divisibilidad.
Actividad de introducción a la relación de divisibilidad.
Múliplos y divisores
Si  y
y 
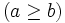 están emparentados por la relación de divisibilidad, es decir,
están emparentados por la relación de divisibilidad, es decir, 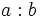 es exacta, entonces decimos que:
es exacta, entonces decimos que:
 es multiplo
es multiplo  y lo expresaremos simbólicamente:
y lo expresaremos simbólicamente: 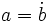 .
.
 es divisor de
es divisor de  y lo expresaremos simbólicamente:
y lo expresaremos simbólicamente: 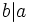 .
.
- La división 60:15=4 es exacta. Entonces 60 es un múltiplo de 15
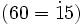 y 15 es un divisor de 60
y 15 es un divisor de 60 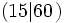 .
.
- Fíjate que 4 también es divisor de 60 porque la división 60:4=15 es también exacta. Por tanto, los divisores siempre van por parejas.
Proposición
Si  es multiplo de
es multiplo de  , entonces existe un número entero
, entonces existe un número entero 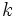 tal que
tal que 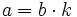 .
.
En efecto, si a es multiplo de b, entonces la división a:b es exacta. Si llamamos k al cociente, se cumple que a=b·k.
¿Cómo se sabe si un número es múltiplo o divisor?
Las definiciones vistas hasta ahora las podríamos haber dado igualmente cambiando números enteros por números naturales. En lo que resta de tema sólo hablaremos de números naturales para evitar duplicidades por cuestiones de signo, sin embargo, todo lo que digamos será también aplicable a números enteros, salvo pequeños matices que obviaremos por cuestiones de simplicidad.
Propiedades
Propiedades de los múltiplos
- Todo número natural es múltiplo de 1 y de sí mismo.
- Todo número natural
 tiene infinitos múltiplos,
tiene infinitos múltiplos, 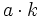 , que se obtienen multiplicándolo por un número natural
, que se obtienen multiplicándolo por un número natural  cualquiera.
cualquiera.
- El 0 es múltiplo de cualquier número.
- La suma de dos o más multiplos de
 es otro múltiplo de
es otro múltiplo de  .
.
- La diferencia de dos múltiplos de un número es otro múltiplo de dicho número.
- Si un número es múltiplo de otro, y éste lo es de un tercero, el primero es múltiplo del tercero.
- Si un número es múltiplo de otro, todos los múltiplos del primero lo son también del segundo.
Propiedades de los divisores
- Todo número natural distinto de cero tiene al menos dos divisores: 1 y él mismo.
- Todo divisor de un número distinto de cero es menor o igual a él. Por tanto, el número de divisores es finito.
- Si un número es divisor de otros dos, también lo es de su suma y de su diferencia.
- Si un número es divisor de otro, también lo es de cualquier múltiplo de éste.
- Si un número es divisor de otro, y éste lo es de un tercero, el primero lo es del tercero.
Múltiplos de un número
La segunda de las propiedades de los múltiplos vista anteriormente me da una forma de calcular los múltiplos de un número natural.
Procedimiento
Para obtener los múltiplos de un número natural  , multiplicaremos
, multiplicaremos  por cada uno de los números naturales:
por cada uno de los números naturales:
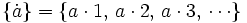
Ejercicio resuelto: Cálculo de los múltiplos de un número
Calcula los múltiplos de 17 comprendidos entre 150 y 200.
Al dividir 150 : 17 obtenemos 8 de cociente y 14 de resto.
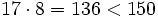
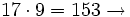 Primer múltiplo de 17 mayor que 150.
Primer múltiplo de 17 mayor que 150.
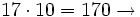 Segundo múltiplo de 17 mayor que 150.
Segundo múltiplo de 17 mayor que 150.
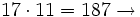 Tercer múltiplo de 17 mayor que 150.
Tercer múltiplo de 17 mayor que 150.
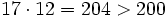 .
.
Qué son y como se obtienen los múltiplos de un número. Ejemplos.
Qué son y como se obtienen los múltiplos de un número. Ejemplos.
Múltiplos de un número entero. Qué son los múltiplos de un número entero, cómo se calculan y como se averigua si un número es múltiplo de otro.
calcula los múltiplo9s de 6 y de 13.
- Actividad para ver algunos múltiplos de un número.
- Actividad en la que deberás separar los números que aparecen según sean múltiplos o no del indicado.
Escribe los cuatro primeros múltiplos de 5, sin contar el cero, ordenados de menor a mayor.
Escribe los cuatro primeros múltiplos de 25, sin contar el cero, ordenados de menor a mayor.
Escribe los cinco primeros múltiplos de 12 mayores que 1000.
Calcula tres múltiplos de 7 comprendidos entre 50 y 100.
Si escribes números cada vez mayores empezando en cero y avanzando de 3 en 3, ¿cuál será el número más cercano, anterior a 400, que alcanzarás?
Marca los números que sean a la vez múltiplos de 3 y de 5.
Ejercicios de autoevaluación sobre múltiplos de un número.
Divisores de un número
Procedimiento
Para encontar todos los divisores de un número,  , buscamos las divisiones exactas
, buscamos las divisiones exactas 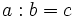 . Entonces
. Entonces  y
y 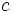 son divisores de
son divisores de  . Para ello procederemos de la siguiente manera:
. Para ello procederemos de la siguiente manera:
- Probaremos con
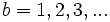 .
.
- Para cada valor de
 que dé división exacta (
que dé división exacta (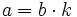 ), tendremos dos divisores:
), tendremos dos divisores:  y
y  .
.
- Pararemos de probar cuando el cociente de la división
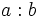 sea menor o igual que
sea menor o igual que  .
.
Ejercicio resuelto: Cálculo de los divisores de un número
Calcula los divisores de 44.
44 : 1 = 44  1 y 44 son divisores. Sigo porque 44 > 1
1 y 44 son divisores. Sigo porque 44 > 1
44 :2 = 22  2 y 22 son divisores. Sigo porque 22 > 2
2 y 22 son divisores. Sigo porque 22 > 2
44 : 3  No es exacta (cociente=14). Sigo porque 14 > 3
No es exacta (cociente=14). Sigo porque 14 > 3
44 : 4 = 11  4 y 11 son divisores. Sigo porque 11 > 4
4 y 11 son divisores. Sigo porque 11 > 4
44 : 5  No es exacta (cociente=8). Sigo porque 8 > 5
No es exacta (cociente=8). Sigo porque 8 > 5
44 : 6  No es exacta (cociente=7). Sigo porque 7 > 6
No es exacta (cociente=7). Sigo porque 7 > 6
44 : 7  No es exacta (cociente=6). Paro porque 6 < 7
No es exacta (cociente=6). Paro porque 6 < 7
Qué son y como se obtienen los divisores de un número. Ejemplos.
En este video podrás ver:
- Divisores de un número.
- Cálculo de los divisores de un número.
Este video también incluye los siguientes contenidos que veremos posteriormente en otro tema:
- Criterios de divisibilidad.
- Números primos y números compuestos.
Calcula los divisores de 50 y de 60.
Calcula los divisores de 120.
¿Cuáles de los siguientes números son divisores de 154?: 3, 5, 6, 9 y 14.
Dos viejos amigos se encuentran y uno de ellos le pregunta al otro:
- ¿Cuántos hijos tienes? - Tres hijas. - ¿Qué edades tienen? - La multiplicación de sus edades es 36 y la suma es igual al número del portal que ves enfrente. - Mmm. Me falta un dato! - Cierto. La mayor toca el piano.
¿Qué edades tienen las hijas?
- Actividad que te muestra todos los divisores de un número dado.
- Actividad en la que debes averiguar todos los divisores de un numero dado.
- Actividad en la que debes separar los divisores de un número de los que no lo son.
Marca en la tabla todos los divisores del número dado.
Actividad en la que deberás hallar los divisores de un número.
Actividad en la que podrás calcular los divisores de un número.
Parejas de divisores de un número.
Nota: En esta actividad se llaman factores a los divisores.
Ejercicios de autoevaluación sobre divisores de un número.
Actividades
Actividades sobre múltiplos y divisores de un número.
Múltiplos y divisores de un número.
Nota: En esta actividad se llaman factores a los divisores.
Múltiplos y divisores de un número.
Nota: En esta actividad se llaman factores a los divisores.
Múltiplos y divisores de un número.
Nota: En esta actividad se llaman factores a los divisores.
Ejercicios de autoevaluación sobre múltiplos y divisores de un número.
|
Actividad: Múltiplos y divisores de un número
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Criterios de divisibilidad
Los siguientes criterios nos permiten averiguar si un número es divisible por otro de una forma sencilla, sin necesidad de realizar una división.
| Divisible por: | Criterio |
|---|---|
| 2 | El número acaba en 0 ó cifra par. |
| 3 | La suma de sus cifras es un múltiplo de 3. |
| 4 | El número formado por las dos últimas cifras es múltiplo de 4. |
| 5 | La última cifra es 0 ó 5. |
| 6 | El número es divisible por 2 y por 3. |
| 7 | La diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es 0 ó un múltiplo de 7. |
| 8 | El número formado por las tres últimas cifras es múltiplo de 8. |
| 9 | La suma de sus cifras es múltiplo de 9. |
| 10 | La última cifra es 0. |
| 11 | Se suman las cifras que forman el número de forma alternativa y se restan los resultados para ver si da un múltiplo de 11 (El cero también lo es) |
Los números que aparecen en verde se corresponden con aquellos cuyo criterio es un proceso que se puede usar de forma recursiva, es decir, si después de aplicarlo no sabemos si el número al que hemos llegado es múltiplo del número en cuestión, podemos aplicar nuevamente el criterio sobre ese resultado.
Criterios de divisibilidad por 2, 3 y 5. Ejemplos.
Criterios para averiguar si un número es divisible por 2, 3, 5, 10 u 11. Ejemplos.
Criterios para averiguar si un número es divisible por 2, 3, 5, 9 u 11. Ejemplos.
Criterios de divisibilidad por 2, 3, 4, 5 y 6. Ejemplos.
Criterios de divisibilidad por 7, 8, 9, 10 y 11. Ejemplos.
Criterios de divisibilidad por 2, 3, 4, 5, 6, 7, 8, 9, 10 y 11. Ejemplos.
Tutorial que explica los criterios de divisibilidad más básicos e importantes, es decir los "trucos" para saber, sin necesidad de dividir, si 2, 3, 5, 7, 11 y 10nson divisores de un número.
- 00:00 a 04:20: Definiciones básicas (divisor).
- 04:20 a 05:55: Criterio de divisibilidad del 2.
- 05:55 a 07:05: Criterio de divisibilidad del 5.
- 07:05 a 09:50: Criterio de divisibilidad de potencias de 10.
- 09:50 a 15:27: Criterio de divisibilidad del 3.
- 15:27 a 21:00: Criterio de divisibilidad del 11.
- 21:00 a 24:50: Criterio de divisibilidad del 7.
Tutorial que explica algunos criterios de divisibilidad más, es decir los "trucos" para saber, sin necesidad de dividir, si 6, 2n, 5n y 9 son divisores de un número.
- 00:00 a 02:20: Definiciones básicas (divisor).
- 02:20 a 05:15: Criterio de divisibilidad de las potencias de 2.
- 05:15 a 07:15: Criterio de divisibilidad de las potencias de 5.
- 07:15 a 10:30: Criterio de divisibilidad del 9.
- 10:30 a 15:46: Criterio de divisibilidad del 6 o producto de primos.
Explicación de por qué funciona el criterio de divisibilidad por 3.
Explicación de por qué funciona el criterio de divisibilidad por 9.
Criterios de divisibilidad por 2
Criterios de divisibilidad por 3
Criterios de divisibilidad por 4
Criterios de divisibilidad por 5
Criterios de divisibilidad por 9
Criterios de divisibilidad por 10
Criterios de divisibilidad por 11
Comprueba si son divisibles por 2, 3, 4, 5, 6, 10, 11 ó 12, los siguientes números: 405, 316, 814, 3080 y 240.
Escribe cuatro números de forma que sean divisibles a la vez entre 2 y 11.
Comprueba si son divisibles por 2, 3, 4, 5, 6, 9 ó 10, los siguientes números: 2 799 588, 5670 y 100 765.
Comprueba si 380 es divisible por 2, 3, 4, 5, 6, 9 ó 10.
- Actividad en la que podrás comprobar si un número dado es múltiplo o no de 2, 3, 4, 5, 6, 8, 9, 10 y 11.
- Actividad en la que deberás separar los números por los que es divisible un número dado.
Actividad sobre criterios de divisibilidad por 2, 3, 5, 7, 9, 10 y 11.
Averigua los múltiplos de 2
Averigua los múltiplos de 3
Averigua los múltiplos de 5
Averigua los múltiplos de 11
Averigua qué número no es múltiplo del dado.
Test de 5 preguntas sobre divisibilidad.
Test de 5 preguntas sobre divisibilidad.
Test de 7 preguntas sobre divisibilidad.
- Criterios de divisibilidad del 2, 3, 5 y 11
Ejercicios de autoevaluación sobre criterios de divisibilidad.
Ejercicios propuestos
|
Ejercicios propuestos: Relación de divisibilidad |