Plantilla:Rectas y puntos notables en un triángulo
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 13:29 30 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 13:42 30 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| + | ===Medianas y baricentro=== | ||
| + | {{Tabla75|celda2=[[Imagen:baricentro.jpg|center|220px]]|celda1= | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
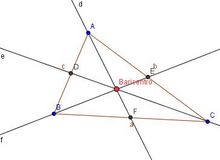
| - | * '''Medianas y baricentro''' | + | *Las '''medianas''' de un triángulo son las rectas que unen cada vértice con el punto medio del lado opuesto. |
| - | {{Tabla75|celda2=[[Imagen:baricentro.jpg|center|220px]]|celda1={{p}} | + | *Las tres medianas se cortan en un punto llamado '''baricentro''' y es el centro de gravedad del triángulo: desde este punto podríamos atarlo con un hilo y quedaría suspendido horizontalmente. |
| - | :Las '''medianas''' de un triángulo son las rectas que unen cada vértice con el punto medio del lado opuesto. | + | }} |
| - | :Las tres medianas se cortan en un punto llamado '''baricentro''' y es el centro de gravedad del triángulo: desde este punto podríamos atarlo con un hilo y quedaría suspendido horizontalmente. | + | |
| {{p}} | {{p}} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| Línea 19: | Línea 20: | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás ver e interactuar con un triángulo y ver su baricentro y sus medianas. | |descripcion=En esta escena podrás ver e interactuar con un triángulo y ver su baricentro y sus medianas. | ||
| - | |enlace=[https://ggbm.at/WxZK4cpG Baricentro]}} | + | |enlace=[https://ggbm.at/WxZK4cpG Baricentro] |
| + | }} | ||
| + | }} | ||
| + | ===Alturas y ortocentro=== | ||
| + | {{Tabla75|celda2=[[Imagen:ortocentro.jpg|center|220px]]|celda1= | ||
| + | {{Caja_Amarilla|texto= | ||
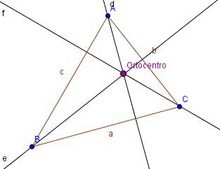
| + | *Ls '''alturas''' de un triángulo son las perpendiculares desde cada vértice al lado opuesto. | ||
| + | *Las tres alturas de un triángulo se cortan en un punto llamado '''ortocentro''' (O). | ||
| }} | }} | ||
| - | {{p}} | ||
| - | * '''Alturas y ortocentro''' | ||
| - | {{Tabla75|celda2=[[Imagen:ortocentro.jpg|center|220px]]|celda1={{p}} | ||
| - | :Las '''alturas''' de un triángulo son las perpendiculares desde cada vértice al lado opuesto. | ||
| - | :Las tres alturas de un triángulo se cortan en un punto llamado '''ortocentro''' (O). | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| Línea 44: | Línea 47: | ||
| }} | }} | ||
| }} | }} | ||
| - | * '''Mediatrices y circuncentro''' | + | ===Mediatrices y circuncentro=== |
| - | {{Tabla75|celda2=[[Imagen:circuncentro.jpg|center|220px]]|celda1={{p}} | + | {{Tabla75|celda2=[[Imagen:circuncentro.jpg|center|220px]]|celda1= |
| - | :Las '''[[Mediatriz de un segmento (1º ESO)|mediatrices]]''' de un triángulo son las perpendiculares a los puntos medios de cada lado. | + | {{Caja_Amarilla|texto= |
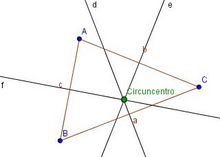
| - | :Las tres mediatrices siempre se cortan en un punto llamado '''circuncentro''', que es el centro de la circunferencia circunscrita al triángulo, que pasa por los tres vértices del triángulo. | + | *Las '''[[Mediatriz de un segmento (1º ESO)|mediatrices]]''' de un triángulo son las perpendiculares a los puntos medios de cada lado. |
| + | *Las tres mediatrices siempre se cortan en un punto llamado '''circuncentro''', que es el centro de la circunferencia circunscrita al triángulo, que pasa por los tres vértices del triángulo. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_8cifras | {{Video_enlace_8cifras | ||
| Línea 60: | Línea 65: | ||
| }} | }} | ||
| }} | }} | ||
| - | * '''Bisectrices e incentro''' | + | ===Bisectrices e incentro=== |
| - | {{Tabla75|celda2=[[Imagen:incentro.jpg|center|220px]]|celda1={{p}} | + | {{Tabla75|celda2=[[Imagen:incentro.jpg|center|220px]]|celda1= |
| - | :Las '''[[Bisectriz de un ángulo (1º ESO)|bisectrices]]''' de un triángulo son las rectas que dividen a sus [[ángulos]] en dos partes iguales. | + | {{Caja_Amarilla|texto= |
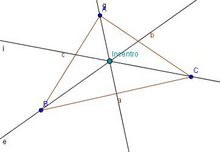
| - | :Las tres '''bisectrices''' de un triángulo cualquiera se cortan en un punto llamado '''incentro''', que es el centro de la circunferencia inscrita al triángulo, que es tangente a los tres lados del triángulo. | + | *Las '''[[Bisectriz de un ángulo (1º ESO)|bisectrices]]''' de un triángulo son las rectas que dividen a sus [[ángulos]] en dos partes iguales. |
| + | *Las tres '''bisectrices''' de un triángulo cualquiera se cortan en un punto llamado '''incentro''', que es el centro de la circunferencia inscrita al triángulo, que es tangente a los tres lados del triángulo. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_8cifras | {{Video_enlace_8cifras | ||
| Línea 76: | Línea 83: | ||
| }} | }} | ||
| }} | }} | ||
| - | * '''Recta de Euler''' | + | {{p}} |
| + | ===Recta de Euler=== | ||
| {{Tabla75|celda2=[[Imagen:recta_euler.jpg|center|220px]]|celda1={{p}} | {{Tabla75|celda2=[[Imagen:recta_euler.jpg|center|220px]]|celda1={{p}} | ||
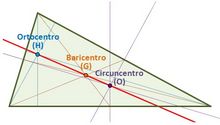
| - | :La recta de Euler de un triángulo es aquella recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo | + | {{Caja_Amarilla|texto= |
| + | La recta de Euler de un triángulo es aquella recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_8cifras | {{Video_enlace_8cifras | ||
| Línea 89: | Línea 99: | ||
| |descripcion=En esta escena podrás ver e interactuar con un triángulo y ver la recta de Euler. | |descripcion=En esta escena podrás ver e interactuar con un triángulo y ver la recta de Euler. | ||
| |enlace=[https://ggbm.at/jakfq7rK Recta de Euler] | |enlace=[https://ggbm.at/jakfq7rK Recta de Euler] | ||
| - | }} | ||
| }} | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ===Actividades y videos=== | ||
| {{AI_anaya | {{AI_anaya | ||
| |titulo1=Elementos notables de un triángulo | |titulo1=Elementos notables de un triángulo | ||
Revisión de 13:42 30 nov 2017
Tabla de contenidos |
Medianas y baricentro
 Medianas y baricentro (8´51") Sinopsis:Medianas y baricentro de un triángulo. Propiedad del baricentro.  Baricentro (construcción) (3´11") Sinopsis:Construcción con regla y compás de las medianas y del baricentro de un triángulo.  Baricentro Descripción: En esta escena podrás ver e interactuar con un triángulo y ver su baricentro y sus medianas. |  |
Alturas y ortocentro
Alturas y ortocentro (7´38") Sinopsis:Alturas y ortocentro de un triángulo según sea rectángulo, acutángulo u obtusángulo. Ortocentro (construcción) (2´48") Sinopsis:Construcción con regla y compás de las alturas y del ortocentro de un triángulo. Ortocentro Descripción: En esta escena podrás ver e interactuar con un triángulo y ver su ortocentro y sus alturas. |  |
Mediatrices y circuncentro
Circuncentro (construcción) (3´12") Sinopsis:Construcción con regla y compás de las mediatrices y del circuncentro de un triángulo. Circuncentro Descripción: En esta escena podrás ver e interactuar con un triángulo y ver su circuncentro y sus mediatrices. |  |
Bisectrices e incentro
Incentro (construcción) (2´43") Sinopsis:Construcción con rtegla y compás de las bisectrices y del incentro de un triángulo. Incentro Descripción: En esta escena podrás ver e interactuar con un triángulo y ver su incentro y sus bisectrices. |  |
Recta de Euler
|
La recta de Euler de un triángulo es aquella recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo. Recta de Euler (construcción) (2´13") Sinopsis:Construcción con regla y compás del ortocentro, baricentro y circuncentro y de la recta de Euler. Recta de Euler Descripción: En esta escena podrás ver e interactuar con un triángulo y ver la recta de Euler. |  |
Actividades y videos
Elementos notables de un triángulo Descripción: Actividades en las que podrás aprender cuáles son los puntos y rectas notables de un triángulo.
Elementos notables de un triángulo Descripción: Actividades en las que podrás aprender cuáles son los puntos y rectas notables de un triángulo.
Elementos notables de un triángulo (5´44") Sinopsis: En este video vamos a estudiar las rectas y puntos notables de un triángulo:
- Rectas: bisectriz, mediana, mediatriz y altura.
- Puntos: incentro, baricentro, circuncentro y ortocentro.
