Números enteros: Definición
De Wikipedia
| Revisión de 13:07 16 dic 2007 Coordinador (Discusión | contribuciones) (→Representación de los números naturales) ← Ir a diferencia anterior |
Revisión de 13:22 16 dic 2007 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 3: | Línea 3: | ||
| |ir= | |ir= | ||
| |ampliar=[http://es.wikipedia.org/wiki/N%C3%BAmero_natural Naturales]<br>[http://es.wikipedia.org/wiki/Numeros_enteros Enteros] | |ampliar=[http://es.wikipedia.org/wiki/N%C3%BAmero_natural Naturales]<br>[http://es.wikipedia.org/wiki/Numeros_enteros Enteros] | ||
| - | |repasar= | + | |repasar=[[Sistemas de numeración (1º ESO) |Sistemas numeración]] |
| - | |enlaces=}}{{p}} | + | |enlaces= |
| + | }} | ||
| + | {{p}} | ||
| ==Números naturales== | ==Números naturales== | ||
| {{Caja Amarilla|texto=El conjunto de los '''números naturales''' es: | {{Caja Amarilla|texto=El conjunto de los '''números naturales''' es: | ||
| Línea 18: | Línea 20: | ||
| |titulo=Números naturales. Números primos | |titulo=Números naturales. Números primos | ||
| |duracion=17´ | |duracion=17´ | ||
| - | |sinopsis=Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos | + | |sinopsis=Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los [[Divisibilidad#Números compuestos y números primos | números primos]]; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. |
| - | números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los [[Divisibilidad#Números compuestos y números primos | números primos]]; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. | + | |
| |video= | |video= | ||
| <center><iframe> | <center><iframe> | ||
Revisión de 13:22 16 dic 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Sistemas numeración | Naturales Enteros | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Números naturales
El conjunto de los números naturales es:
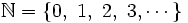
Son infinitos y sirven para contar (números cardinales: 1, 2, 3, ...) o para ordenar (números ordinales: 1º, 2º, 3º, ...).
Representación de los números naturales
Podemos representarlos en una recta:
Video: Números naturales. Números primos (17´)
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía.
Números enteros
El conjunto de los números enteros es
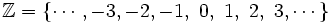
|
Actividad Interactiva: Números enteros
Actividad 1. Introducción al conjunto de los números enteros.
Actividad: En la escena adjunta te presentamos unos ejemplos en los que se muestra la necesidad de utilizar números enteros. Sigue las instrucciones que te van apareciendo en escena y anota los ejemplos en tu cuaderno. |
Representación de los números enteros
Podemos representarlos en una recta:
|
Actividad Interactiva: Representación de los números enteros
Actividad 1. Representación de los números enteros en la recta numérica.
Actividad: En esta escena vas a conocer como se representan los números enteros en la recta numérica. |
Orden en el conjunto de los enteros
En la representación de los enteros en la recta numérica se observa el orden que existe en el conjunto de los números enteros, siendo los números negativos menores que los positivos y que el cero.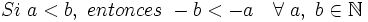
|
Actividades Interactivas: Orden en los números enteros
1. ¿Cómo se ordenan los números enteros?.
Actividad: En esta escena aprenderás a comparar números enteros. Anota lo que aprendas en tu cuaderno. Lee atentamente las indicaciones. Pulsa INICIO cada vez que quieras ver un ejemplo nuevo.
2. Autoevaluación.
Actividad: En esta escena deberas decir que número es el mayor. Anota los resultados en tu cuaderno. Pulsa INICIO cada vez que quieras ver un ejemplo nuevo. |
Ejercicios
|
Ejercicios: Orden en los enteros
1. Ordena los siguientes números enteros: -3, -16, 2, -7, 9, 0.
Solución: − 16 < − 7 < − 3 < 0 < 2 < 9 |



