Números enteros: Operaciones
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Naturales Enteros I Enteros II Potencias | Enteros | WIRIS Geogebra Calculadora |
Las operaraciones con enteros son similares a las operaciones con naturales, pero con las peculiaridades que aportan los números negativos.
Tabla de contenidos |
Opuesto de un entero
El opuesto de un número entero,  , es otro número entero,
, es otro número entero, 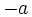 , simétrico de
, simétrico de  respecto del cero. En consecuencia, se encuentra a la misma distancia del cero que
respecto del cero. En consecuencia, se encuentra a la misma distancia del cero que  , pero tiene signo contrario. Lo escribiremos
, pero tiene signo contrario. Lo escribiremos 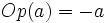 .
.
Es obvio que si 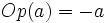 entonces
entonces 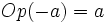 , y viceversa. Por eso, también se dice que
, y viceversa. Por eso, también se dice que  y
y 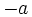 son números opuestos.
son números opuestos.
Concepto de opuesto de un número entero. Ejemplos.
Concepto de opuesto de un número entero. Ejemplos.
Opuesto de un número entero. Representación en la recta numérica.
Uso del signo "menos" para la obtención del opuesto de un número entero.
Ejercicios sobre números opuestos.
- Actividad en la que podrás ver la relación entre un número y su opuesto mediante su representación en la recta real.
- Actividad en la que deberás obtener el opuesto de un número entero.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
|
Actividad: Opuesto de un número entero
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Valor absoluto de un entero
El valor absoluto de un número entero  se representa por
se representa por 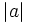 y se define de la siguiente manera:
y se define de la siguiente manera:
- Si el número es positivo, su valor absoluto es él mismo.
- Si el número es negativo, su valor absoluto es igual a su opuesto.
Propiedades
- El valor absoluto de un número es la distancia que lo separa del cero en la recta numérica.
- El valor absoluto de un número siempre es positivo o cero.
- El valor absoluto de cero es cero.
Valor absoluto de un número entero. Interpretación métrica.
- Representación de los números enteros en la recta real.
- Valor absoluto de un número entero. Interpretación métrica.
Valor absoluto de un número entero. Ejemplos.
Valor absoluto de un número entero. Ejemplos.
Valor absoluto de un número entero. Ejemplos.
En este video vamos a ver lo que es el valor absoluto de un número entero y también vamos a aprender a calcularlo.
Valor absoluto de un entero.
Valor absoluto como distancia entre números.
Halla 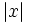 , cuando
, cuando 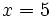 ,
, 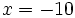 y
y 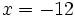 .
.
Compara:
- a)
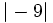 y
y 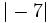
- b)
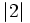 y
y 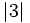
- c)
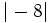 y
y 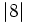
- d)
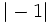 y
y 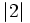 .
.
Ordena de menor a mayor: 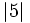 ,
, 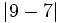 ,
, 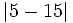 ,
, 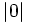 y
y 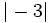 .
.
- Actividad en la que puedes obtener el valor absoluto de un número entero.
- Actividad en la que deberás obtener el valor absoluto de un número entero.
Aprende a pensar el valor absoluto como la distancia a cero, y practica encontrar valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Halla el valor absoluto.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Compara valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Cálculo de distancias mediante valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Suma y resta de enteros
Tutorial en el que se explica a través de varios ejemplos la suma y resta de números enteros, desde el caso en el que sólo intervienen dos números hasta cuando intervienen más, con o sin paréntesis.
- 00:00 a 10:45: Suma y Resta simple de número enteros.
- 10:45 a 12:50: Ejercicios de Suma y Resta simple.
- 12:50 a 21:21: Suma y Resta compuesta de números enteros.
- 21:21 a 25:27: Ejercicios de Suma y Resta compuesta.
Suma y resta de dos números enteros
Sabemos que los números enteros pueden tener signo positivo (un más o nada delante del número) o signo negativo (un menos delante del número). Sin embargo, cuando dos enteros aparecen juntos, sus signos expresan una operación.
- Suma: Siempre que vemos dos enteros juntos, sin más separación entre ellos que sus signos, lo que tenemos delante es una suma. Para realizar esa suma puedes guiarte por la lógica: los números negativos representan pérdidas, los positivos ganancias y el resultado de la operación es el balance entre ganancias y pérdidas.
- Resta: La resta de números enteros es el resultado de sumar el primero con el opuesto del segundo.
Por ejemplo, si vemos escrito:
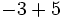
sabemos que uno es negativo y el otro es positivo, pero al mismo tiempo estamos indicando una cuenta. Algo así como "perdemos 3, pero ganamos 5". Lógicamente, el resultado es que "ganamos 2", es decir:
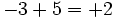
Lo que realmente sucede es que estamos haciendo una suma de número enteros, pero omitimos el símbolo de la operación, por economía del lenguaje. En realidad deberíamos escribir:
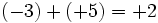
Siguiendo esa lógica de balance entre pérdidas y ganancias, para sumar números enteros seguiremos las siguientes reglas:
Procedimiento: Suma de números enteros
Dependiendo del signo de los dos números a sumar, tenemos que:
- Si tienen el mismo signo, se suman los valores absolutos y se pone el mismo signo que tenían los números.
- Si tienen distinto signo, se restan los valores absolutos (el mayor valor absoluto menos el menor) y se pone el signo del que tenga mayor valor absoluto.
- a)
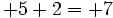
- b)
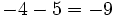
- c)
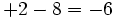
- d)
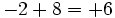
¿Qué pasa en cada situación?
- En el primero los dos son positivos (ganancias) y el resultado es la suma de esas ganancias.
- En el segundo los dos son negativos (pérdidas) y el resultado es la suma de esas pérdidas.
- En el tercero tienen signos distintos, pero las pérdidas son mayores que las ganancias, así que el resultado es negativo.
- En el cuarto tienen signos distintos, pero las ganancias son mayores que las pérdidas, así que el resultado es positivo.
Tutorial que usa el símil de las batallas entre soldados para explicar la suma de números enteros, según tengan o no el mismo signo.
Ejemplo sobre lo explicado en el tutorial anterior.
El mismo ejemplo del tutorial 1b por otro método (agrupando primero los del mismo signo).
Un error frecuente.
Ejemplos de como se suman números enteros, según tengan o no el mismo signo.
Ejemplos de como se suman números enteros, según tengan o no el mismo signo, usando la recta numérica.
Suma de números enteros.
Resta de números enteros.
Suma de números enteros.
Resta de números enteros.
Interpretación geométrica de la suma de números enteros.
Suma y resta de números enteros.
Calcula:
a) 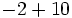 b)
b) 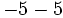 c)
c) 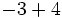 d)
d)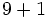
e) 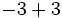 f)
f) 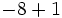 g)
g) 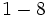 h)
h) 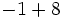 i)
i) 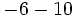
- Actividad en la que se te plantean problemas para practicar la suma y resta de dos números enteros.
- Actividad para calcular la suma o resta de dos números enteros.
Suma y resta de dos números enteros.
Suma y resta de dos números enteros.
Suma de dos números enteros.
Suma y resta de más de dos números enteros
Cuando sumemos más de dos números enteros podemos proceder de dos formas:
- Método 1: Sumar los positivos por un lado y los negativos por otro y, después, efectuar la resta de los resultados.
- Método 2: Ir sumando o restando paso a paso, de izquierda a derecha.
Ejemplos de como se suman más de dos números enteros por los 2 métodos antes descritos.
Ejemplos de como se suman números enteros, según tengan o no el mismo signo, usando la recta numérica.
Calcula:
a) 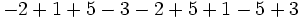
b) 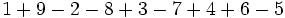
Calcula:
a) 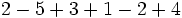
b) 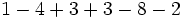
c) 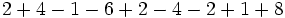
- Actividad en la que se te plantean problemas para practicar la suma y resta de tres números enteros por dos métodos.
- Actividad para calcular la suma o resta de tres números enteros.
Actividad para calcular la suma de más de tres números enteros.
Actividad para calcular la suma de más de tres números enteros.
Sumas y restas con paréntesis
Al operar, no pueden juntarse dos signos. Se deben separar con paréntesis y se aplicarán las siguientes reglas:
Sumas y restas de números enteros con paréntesis. Ejemplos.
Sumas y restas de números enteros cambiando el signo de los números que hay dentro del parentesis antes de operar.
Sumas y restas de números enteros. Ejemplos.
Escritura simplificada de la suma y resta de los números enteros. Equivalencia de los números enteros positivos con los números naturales. Cómo sacar los paréntesis en las sumas y en las restas. Cómo aplicar la regla de los signos de la multiplicación para eliminar los paréntesis en sumas y restas.
¿Por qué restar un negativo equivale a sumar un positivo?
Sumas de enteros con el mismo signo:
Sumas de enteros con distinto signo:
Sumas y restas con enteros:
- Actividad en la que se te muestran ejemplos de expresiones sencillas de números enteros con paréntesis.
- Actividad para calcular expresiones sencillas de números enteros con paréntesis.
- Actividad en la que se te muestran ejemplos de sumas y restas de dos números enteros con paréntesis.
- Actividad para calcular sumas y restas de dos números enteros con paréntesis.
Suma y resta de 2 números enteros:
Actividades de autoevaluación sobre sumas de dos números enteros.
Actividades de autoevaluación sobre sumas de dos números enteros.
Actividades de autoevaluación sobre sumas y restas de dos números enteros.
Suma de dos números enteros.
Resta de dos números enteros.
En esta escena podrás practicar las sumas y restas con 2 números enteros.
Si tienes problemas con la actividad a la hora de escribir las soluciones en los recuadros, haz lo siguiente:
- Haz click con el ratón en el cuadro donde va la repuesta.
- Pulsa "Enter".
- Te aparecerá el cursor y ya podrás escribir la solución.
Suma y resta de 3 o más números enteros:
Suma y resta de tres números enteros.
Actividades de autoevaluación sobre sumas de cuatro números enteros.
Actividades de autoevaluación sobre restas de cuatro números enteros.
Actividades de autoevaluación sobre restas de cuatro números enteros.
En esta escena podrás practicar las sumas y restas con 4 números enteros.
Si tienes problemas con la actividad a la hora de escribir las soluciones en los recuadros, haz lo siguiente:
- Haz click con el ratón en el cuadro donde va la repuesta.
- Pulsa "Enter".
- Te aparecerá el cursor y ya podrás escribir la solución.
Procedimiento para quitar paréntesis
- A) Si dentro del paréntesis tenemos varias sumas y restas podemos proceder de dos formas:
- Método 1: Efectuar las operaciones dentro del paréntesis hasta que quede un solo número entero en su interior y a continuación proceder siguiendo las reglas anteriormente vistas.
- Método 2: Si delante del paréntesis hay un signo más (+), se quitaran los paréntesis dejando los números del interior con el mismo signo. Pero si delante hay un signo menos (-), los números de dentro cambiarán de signo.
- B) Si hay paréntesis dentro de otros paréntesis (o corchetes), se efectuaran primero los más interiores.
Sumas de enteros con paréntesis:
Restas de enteros con paréntesis:
Sumas y restas de enteros con paréntesis:
Sumas y restas de enteros con paréntesis.
Sumas y restas de números enteros con paréntesis y corchetes.
Completa los recuadros y cuando termines pulsa en el botón "Corregir" que tienes en la parte inferior de la escena. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Ejercicios de autoevaluación sobre sumas y restas de enteros con paréntesis con dificultad seleccionable.
Operaciones combinadas con enteros
|
Actividad: Operaciones combinadas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Tutorial en el que se explica a través de varios ejemplos el orden en el que hay que realizar las operaciones con números, lo que se llama la jerarquía de operaciones.
- 00:00 a 03:47 : Conceptos básicos. Jerarquía de operaciones.
- 03:47 a 19:37 : Ejercicios de Operaciones Combinadas.
Operaciones combinadas con enteros.
Efectúa:
a) 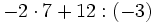
b) 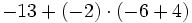
c) ![(-30):15-3 \cdot [(-3)+(-8)]\;](/wikipedia/images/math/e/6/8/e68cbfa29c5b2441d196f58e5650e229.png)
d) ![-2+4:[7+(-6):2]\;](/wikipedia/images/math/7/8/9/789c45348313c9a5a97d88770e651174.png)
e) 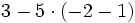
f) ![5+(-24):(+6)+5 \cdot [4-(-2) \cdot (+3)]\;](/wikipedia/images/math/3/2/e/32e813821a2ebe77944b02c2111bde3c.png)
Efectúa:
a) 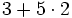
b) 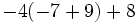
c) 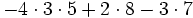
d) 
Efectúa:
a) 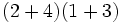
b) 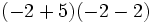
c) 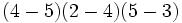
d) ![-2+[3+2(-3-1)]\;](/wikipedia/images/math/2/2/5/225a550a5c715d1274f269774c6cac8c.png)
e) ![-2{5-2[3-4+(1+2)-2(-1-1)]-3}+1\;](/wikipedia/images/math/f/1/7/f1746b8cc35742adcd78520262157f86.png)
Efectúa:
Efectúa:
a) 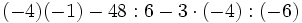
b) ![(-6):(+2)+[18-9:(+3)]\cdot (-2+4)+5 \cdot (-7)\;](/wikipedia/images/math/0/f/1/0f12794504f2a70e93d1f1a7d0f27e72.png)
Efectúa:
a) ![(-7)-\{9-[(-7)+(-13)-(-5)]+[23-(+18)+(-6)]\}\;](/wikipedia/images/math/8/5/f/85fda0cee7c9c7b7f463a471512b0756.png)
b) 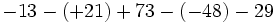
c) ![1-\{4-[-2+(5-1-9)-1]+2\}+3\;](/wikipedia/images/math/6/d/5/6d5616771a67c61c00a77f7b152ddae5.png)
Efectúa:
Efectúa:
Efectúa:
Efectúa:
Efectúa:
Efectúa:
Ejercicios resueltos de operaciones combinadas con números enteros.
En esta escena podrás practicar las operaciones con números enteros: suma, resta, multiplicación, cociente, potencia y raíz; con o sin paréntesis.
En esta escena podrás practicar las operaciones de suma, resta y multiplicación con paréntesis con 3 números enteros.
En esta escena podrás practicar las operaciones combinadas con paréntesis con 3 números enteros.
En esta escena podrás practicar las operaciones combinadas con paréntesis con 4 números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros con ayuda de la calculadora. (nivel 1)
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros con ayuda de la calculadora. (nivel 2)
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros. No incluye potencias ni raíces.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros. Incluye raíces y potencias.
Calculadora
Suma, resta, multiplicación y división
|
Calculadora: Suma, resta, multiplicación y división |
Opuesto
|
Calculadora: Opuesto |
Paréntesis
|
Calculadora: Paréntesis |
Potencias
|
Calculadora: Potencias |
Wiris
WIRIS: Operaciones con números naturales
Utiliza el editor para calcular:
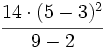
Comprueba el resultado también con tu calculadora. (Solución: 8)
Ejercicios y problemas
Ejercicios
Breve repaso de las operaciones con enteros
|
Actividad: Operaciones con enteros
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Problemas
|
Problemas: Operaciones con enteros
1. Estamos en la planta 345 de un gran rascacielos del futuro y bajamos en ascensor a la planta -15. ¿Cuánto tiempo tardaremos si el ascensor tarda 1 segundo en bajar 5 pisos?
Solución: 1' 12"
2. Pitágoras, filósofo y matemático griego, nació el año 582 a.C. ¿Cuántos años han pasado hasta el año 2007 d.C.?
Solución: 2.588 años, ya que no existió el año 0.
3. Durante el ascenso a una montaña, la temperatura desciende 2 grados cada 200 m de ascenso. ¿A qué altura habrá que ascender para alcanzar -15ºC, si en el punto de partida, la temperatura es de 5ºC y este está a una altitud de 300 m?
Solución: 2.300 m. |
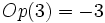 (El opuesto de 3 es -3).
(El opuesto de 3 es -3).
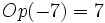 (El opuesto de -7 es 7).
(El opuesto de -7 es 7).
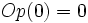 (El opuesto de 0 es 0).
(El opuesto de 0 es 0).
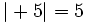
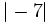
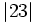
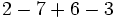
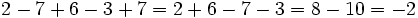
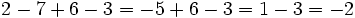
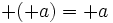
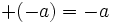
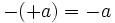
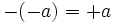
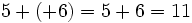
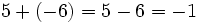
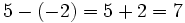
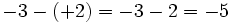
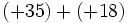

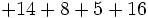
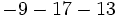
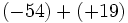
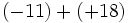
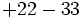
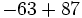
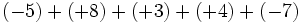
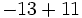
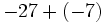
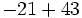
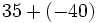
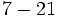
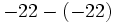
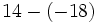
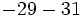
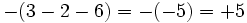
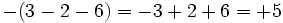
![11-[7-(3-6)+(6-4)]\,](/wikipedia/images/math/7/4/1/741e8e561e2a54a907a8ada8072eaa26.png)
![11-[7- (-3) + 2]\,](/wikipedia/images/math/4/b/2/4b2f021cc9a3932553a1952e4ee05172.png)
![11-[7 + 3 + 2]\,](/wikipedia/images/math/6/5/6/656c546483eaf7bdd7c561c5493d0dda.png)
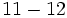
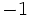
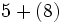
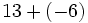
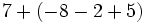
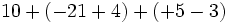
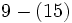
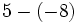
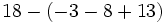
![-{13-[-(23-12)+18]-27}\;](/wikipedia/images/math/a/1/0/a104371813ad27298314c9edb5d0e6b1.png)
![(10-15)-[9-(23-12)]+(-27)\;](/wikipedia/images/math/c/0/5/c055c0c484af14bc32eb063913ecc082.png)
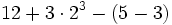
![[8-(-6)]:(+7)+(-9)\;](/wikipedia/images/math/d/7/d/d7d0b31fafbbbb0b156edb34e487cae3.png)
![18-(-2) \cdot[(+15):(8-11)]\;](/wikipedia/images/math/1/9/7/197dff4d42e5917261deea7756fe42d6.png)
![[8 + 6]:(+7)+(-9)\;](/wikipedia/images/math/8/4/e/84e6eb1dd9731dd92e13d5c09ecceff7.png)
![[14]:(+7)+(-9)\;](/wikipedia/images/math/b/8/5/b855f17314d0124a839a03b9c58ddfde.png)
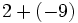
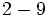
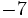
![18-(-2) \cdot[(+15):(-3)]\;](/wikipedia/images/math/b/f/f/bffdcd0011c95a2677f2441ab7af0bee.png)
![18-(-2) \cdot [-5]\;](/wikipedia/images/math/5/c/e/5cef9b8165c728c79e1c10031ec145c7.png)
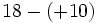
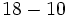
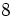
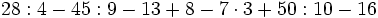
![8-\{7-[15-(6-9+1)-(3 \cdot 4-17)]\}-(-5+1)\;](/wikipedia/images/math/2/8/1/281c6dff8b881adee343ddf08db0c8ba.png)
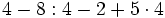
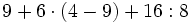
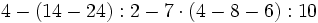
![25+40:(6-4)+[5-(8-9)]\;](/wikipedia/images/math/2/6/d/26d0311df03f52854ef572a315ff4fea.png)
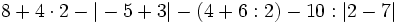
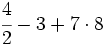
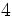


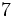
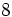
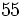
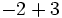
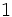
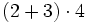
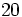
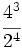
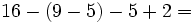
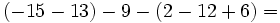
![(-3) \cdot [5 \cdot (8-6) -3 \cdot (3-7)]=](/wikipedia/images/math/f/5/9/f59deb2e37e79d7962fd952b00c1a69b.png)

