Números enteros: Operaciones
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Naturales Enteros I Enteros II Potencias | Enteros | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Introducción
Un toque divertido para empezar el tema:
Troncho no quiere saber nada de números naturales, ni enteros, ni como se opera con ellos.
Puedes encontrar ejercicios sobre este vídeo y material similar en: http://www.angelitoons.com/
Las operaraciones con enteros son similares a las operaciones con naturales, pero con las peculiaridades que aportan los números negativos. Veamos un video a modo de introducción.
Breve resumen de las operaciones con enteros.
Suma y resta de enteros
Suma y resta de dos números enteros
Sabemos que los números enteros pueden tener signo positivo (un más o nada delante del número) o signo negativo (un menos delante del número). Sin embargo, cuando dos enteros aparecen juntos, sus signos expresan una operación.
- Suma: Siempre que vemos dos enteros juntos, sin más separación entre ellos que sus signos, lo que tenemos delante es una suma. Para realizar esa suma puedes guiarte por la lógica: los números negativos representan pérdidas, los positivos ganancias y el resultado de la operación es el balance entre ganancias y pérdidas.
- Resta: La resta de números enteros es el resultado de sumar el primero con el opuesto del segundo.
Por ejemplo, si vemos escrito:
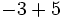
sabemos que uno es negativo y el otro es positivo, pero al mismo tiempo estamos indicando una cuenta. Algo así como "perdemos 3, pero ganamos 5". Lógicamente, el resultado es que "ganamos 2", es decir:
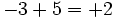
Lo que realmente sucede es que estamos haciendo una suma de número enteros, pero omitimos el símbolo de la operación, por economía del lenguaje. En realidad deberíamos escribir:
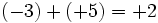
Siguiendo esa lógica de balance entre pérdidas y ganancias, para sumar números enteros seguiremos las siguientes reglas:
Procedimiento: Suma de números enteros
Dependiendo del signo de los dos números a sumar, tenemos que:
- Si tienen el mismo signo, se suman los valores absolutos y se pone el mismo signo que tenían los números.
- Si tienen distinto signo, se restan los valores absolutos (el mayor valor absoluto menos el menor) y se pone el signo del que tenga mayor valor absoluto.
- a)
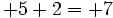
- b)
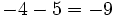
- c)
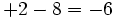
- d)
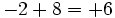
¿Qué pasa en cada situación?
- En el primero los dos son positivos (ganancias) y el resultado es la suma de esas ganancias.
- En el segundo los dos son negativos (pérdidas) y el resultado es la suma de esas pérdidas.
- En el tercero tienen signos distintos, pero las pérdidas son mayores que las ganancias, así que el resultado es negativo.
- En el cuarto tienen signos distintos, pero las ganancias son mayores que las pérdidas, así que el resultado es positivo.
Tutorial que usa el símil de las batallas entre soldados para explicar la suma de números enteros, según tengan o no el mismo signo.
Ejemplo sobre lo explicado en el tutorial anterior.
El mismo ejemplo del tutorial 1b por otro método (agrupando primero los del mismo signo).
Un error frecuente.
Ejemplos de como se suman números enteros, según tengan o no el mismo signo.
Ejemplos de como se suman números enteros, según tengan o no el mismo signo, usando la recta numérica.
Suma de números enteros.
Resta de números enteros.
Suma de números enteros.
Resta de números enteros.
Interpretación geométrica de la suma de números enteros.
Suma y resta de números enteros.
Calcula:
a) 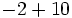 b)
b) 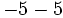 c)
c) 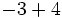 d)
d)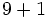
e) 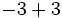 f)
f) 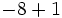 g)
g) 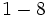 h)
h) 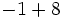 i)
i) 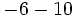
- Actividad en la que se te plantean problemas para practicar la suma y resta de dos números enteros.
- Actividad para calcular la suma o resta de dos números enteros.
Suma y resta de dos números enteros.
Suma y resta de dos números enteros.
Suma de dos números enteros.
Suma y resta de más de dos números enteros
Cuando sumemos más de dos números enteros podemos proceder de dos formas:
- Método 1: Sumar los positivos por un lado y los negativos por otro y, después, efectuar la resta de los resultados.
- Método 2: Ir sumando o restando paso a paso, de izquierda a derecha.
Ejemplos de como se suman más de dos números enteros por los 2 métodos antes descritos.
Ejemplos de como se suman números enteros, según tengan o no el mismo signo, usando la recta numérica.
Calcula:
a) 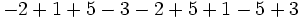
b) 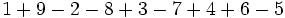
Calcula:
a) 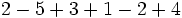
b) 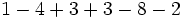
c) 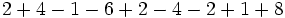
- Actividad en la que se te plantean problemas para practicar la suma y resta de tres números enteros por dos métodos.
- Actividad para calcular la suma o resta de tres números enteros.
Actividad para calcular la suma de más de tres números enteros.
Actividad para calcular la suma de más de tres números enteros.
Propiedades de la suma y de la resta de números enteros
Propiedades de la suma
- Operación interna: el resultado de sumar dos números enteros es otro número entero.
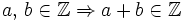
- Propiedad conmutativa: La suma no varía al cambiar el orden de los sumandos.
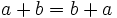
- Propiedad asociativa: El resultado de la suma es independiente de la forma en que se agrupen los sumandos.
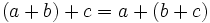
- Elemento neutro: El elemento neutro para la suma es el 0.
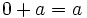
- Elemento opuesto: Todo número entero,
 , tiene un opuesto,
, tiene un opuesto, 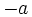 , que al sumarse con él da el elemento neutro.
, que al sumarse con él da el elemento neutro.
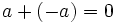
Conmutativa:
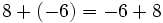
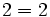
Asociativa:

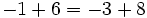
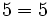
Elemento neutro:
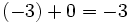
Elemento opuesto:
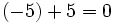
Esto es, el opuesto de 5 es -5 y el opuesto de -5 es 5. Por tanto, decimos que 5 y -5 son opuestos.
Propiedades de la suma de números enteros. Ejemplos (1ª parte)
1) Calcula:
- a) (-5)+(+7)
- b) (+3)+(-2)
- c) (-2)+(+4)+(+3)
- d) (-7)+(-5)+(-1)
- e) (-3)+(-9)+(-6)
2) Completa la tabla: (Ejercicio sobre el opuesto de un número entero)
3) Completa:
- a) (-7)+ ... = 0
- b) (+4)+ ... = 0
- c) ... +(-5) = 0
- d) ... +(+3) = 0
4) Transforma las restas en sumas y después calcula:
- a) (+5)-(-3) =
- b) (+4)-(+2) =
- c) (+8)-(-8) =
5) Calcula:
- a) (-6)-(+3) =
- b) (+3)-(-6) =
Observando esto, ¿tiene la resta la propiedad conmutativa?
1) Calcula:
- a) (+5)-[(+4)-(-5)]=
- b) [(+5)-(+4)]-(-2)=
Observando esto, ¿tiene la resta la propiedad asociativa?
2) Calcula:
- a) Op[(+5)+(+3)]=
- b) Op[(-4)+(-2)]=
- c) Op[(-5)+(-2)]=
- d) Op[Op(-5)]=
3) Calcula Op[(-5)-(+2)].
4) Contesta:
- a) ¿Cuál es el opuesto del opuesto de -3?
- b) ¿Y el opuesto del opuesto de +5?
1) Calcula:
- a) (+7)+(-3)+(-4)=
- b) (+5)+(-4)+(-2)=
- c) (-3)+(-5)+(-4)=
- d) (-7)+(-10)+(-3)=
2) Calcula:
- a) (-5)-(-8)=
- b) (-20)-(-40)=
- c) (+55)-(-25)=
- d) (-35)-(-55)=
3) Calcula:
- a) -(-3)=
- b) -(-5)=
- c) -(-20)=
- d) -(-17)=
4) ¿Qué propiedades de la suma se dan en las siguientes igualdades?
- a) (+5)+(-3) = (-3)+(+5)
- b) (-7)+0- = -7
- c) [(+1)+(-4)]+(+2) = (+1)+[(-4)+(+2)]
- d) (+15)+(-15) = 0
5) Contesta:
- a) ¿Cuál es el elemento neutro de la suma de números enteros? ¿Por qué?
- b) Calcula el opuesto del opuesto de 3. ¿Cuál es el opuesto del opuesto de un número entero?
- c) ¿Puede ser la diferencia de dos números enteros negativos un número entero positivo? Pon ejemplos.
- d) ¿Cuál es la suma de dos números opuestos?
- e) ¿Tiene la resta de números enteros la propiedad conmutativa? Pon un ejemplo.
- f) ¿Qué propiedad de la suma de números enteros no la tiene la suma de números naturales?
- g) ¿En qué parte de la recta están situados los opuestos de los números enteros positivos?
Propiedades de la resta
- Operación interna: el resultado de restar dos números enteros es otro número entero.
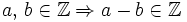
- Propiedad conmutativa: No se cumple
- Propiedad asociativa: No se cumple
Multiplicación o producto de números enteros
Regla de los signos para el producto
- Si dos números enteros tienen el mismo signo su producto es un entero positivo.
- Si dos números enteros tienen distinto signo, el producto es un entero negativo.
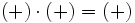 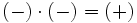 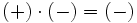 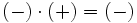 |
- Los paréntesis aparecen para separar los símbolos · y : de los símbolos + y -.
- Si el primer número es negativo no hace falta poner paréntesis.
- Cuando el signo (positivo) del segundo número no aparece escrito los paréntesis no son necesarios.
- a)
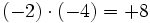
- b)
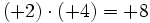
- c)

- d)
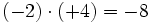
Aunque las expresiones anteriores son correctas, si nos atenemos a las reglas anteriores, los ejemplos b), c) y d) se podrían haber escrito de la siguiente manera más simple:
- b)
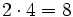
- c)
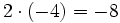
- d)
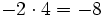
Producto de números enteros. Regla de los signos. Ejemplos
Producto de números enteros.
Aprende a usar la regla de los signos para multiplicar números enteros.
When number systems were expanded to include negative numbers, rules had to be formulated so that multiplication would be consistent regardless of the sign of the operands.
(Disponibles los subtítulos en inglés)
Opera:
- Actividad en la que se plantean problemas para aprender a multiplicar números enteros.
- Actividad para practicar la multiplicación de números enteros.
Practica el producto de números enteros
En esta escena podrás practicar la multiplicación de números enteros.
Si tienes problemas con la actividad a la hora de escribir las soluciones en los recuadros, haz lo siguiente:
- Haz click con el ratón en el cuadro donde va la repuesta.
- Pulsa "Enter".
- Te aparecerá el cursor y ya podrás escribir la solución.
Ejercicios de autoevaluación sobre multiplicaciones de números enteros.
Propiedades del producto de números enteros
Propiedades de la multiplicación
- Operación interna: El producto de dos números enteros es otro número entero:
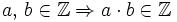
- Propiedad conmutativa: El producto no varía al cambiar el orden de los factores.
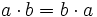
- Propiedad asociativa: El resultado de una multiplicación es independiente de la forma en que se agrupen los factores.
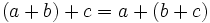
- Propiedad distributiva: El producto de un número por una suma (o resta) es igual a la suma (o resta) de los productos del número por cada sumando.

- Elemento neutro: El elemento neutro para la multiplicación es el 1.
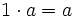
Gracias a la propiedad distributiva, tenemos dos opciones a la hora de enfrentarnos a unos paréntesis:
- Podemos realizar primero las operaciones que aparezcan dentro de los paréntesis.
- Podemos aplicar la propiedad distributiva y eliminar los paréntesis sin completar las operaciones que aparezcan dentro de ellos.
Esta propiedad es clave para realizar operaciones combinadas que veremos proximamente.
La propiedad distributiva tiene una especie de propiedad "recíproca" que llamaremos sacar factor comun. En realidad es la misma propiedad, pero usada "al revés". La idea es buscar un divisor común a todos los sumandos que tengamos y "sacarlo" fuera del paréntesis en el que meteremos al resultado de dividir a cada uno de los sumandos por ese factor.
- a) En este primer ejemplo sacaremos 3 como factor común:
- b) En este otro sacaremos 5 como factor común:
Sacar factor común no nos será especialmente útil en este tema, sin embargo, si será de gran utilidad, más adelante, cuando trabajemos con expresiones algebraicas.
- Propiedades del producto de números enteros. Ejemplos.
- Ejercicios:
1) Calcula:
- a)
![[(-4) \cdot (-2)] \cdot 6\;](/wikipedia/images/math/4/4/a/44a47677fd91afc7f8ed6c96632ec942.png)
- b)
![(-4) \cdot [(-2)] \cdot 6]\;](/wikipedia/images/math/b/1/9/b1976f580931741859d782c6d3346a15.png)
- c)
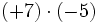
- d)
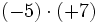
1) Calcula:
- a)
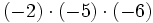
- b)
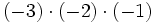
- c)
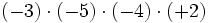
- d)
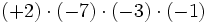
2) Calcula:
- a)
![[(-7) + (-3)] \cdot (+2)\;](/wikipedia/images/math/3/4/5/345ca286da82e44f4d7417853d6141b5.png)
- b)
![[(+4) - (+5)] \cdot (-3)\;](/wikipedia/images/math/6/d/6/6d6c19c9fa1c521567b33701a91f3a7c.png)
- c)
![(-5) \cdot [(+9) - (-5)]\;](/wikipedia/images/math/c/3/e/c3edcc45ed3f7456bfa1673b3a0d4f8a.png)
- d)
![(+2) \cdot [(+5) + (-2)]\;](/wikipedia/images/math/2/8/5/2856468702b11cb88edb046851bd6089.png)
3) Saca factor común:
- a)
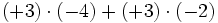
- b)
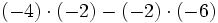
- c)
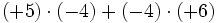
- d)
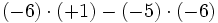
4) Sabiendo que a=-2, b=-3 y c=-1, calcula:
- a)
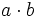
- b)

- c)
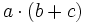
- d)
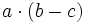
5) Completa la tabla (Ejercicios con operaciones y valor absoluto de números enteros)
6) Saca factor común descomponiendo previamente en producto de factores:
- a)
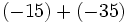
- b)
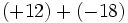
- c)
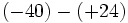
- d)
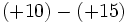
Ejercicios de autoevaluación sobre la propiedad distributiva del producto de enteros.
Ejercicios de autoevaluación sobre sacar factor común.
División o cociente de números enteros
Regla de los signos para el cociente
Con la división , al igual que con la multiplicación, se aplica la misma regla de los signos:
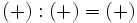 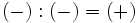 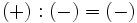 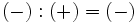 |
División o cociente de números enteros. Ejemplos.
División o cociente de números enteros. Ejemplos.
Cociente de números enteros.
- Actividad para aprender a dividir números enteros.
- Actividad para practicar la división de números enteros.
Practica el cociente de números enteros.
Ejercicios de autoevaluación sobre divisiónes de números enteros.
Propiedades de la división de números enteros
Propiedades de la división de números enteros
- La división de de números enteros no siempre es un número entero.
- La división de números enteros no tiene las mismas propiedades que producto. No tiene la propiedad conmutativa, ni la asociativa, ni la distributiva.
Al no tener la división de números enteros la propiedad asociativa, si aparecen varias divisiones consecutivas, sin paréntesis, tienen que hacerse de izquierda a derecha.
Fíjate en las siguientes operaciones:
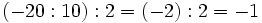
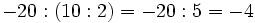
Por tanto, la división no es asociativa, así que si nos encontramos una cuenta como la de este ejemplo, pero sin paréntesis, tendremos que hacer las divisiones de izquierda a derecha, sin alterar el orden.
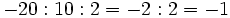
Ejercicios de autoevaluación sobre las propiedades del producto y cociente de números enteros.
Actividades y videotutoriales
Multiplicación y división de enteros. Regla de los signos.
Tutorial en el que se explica a través de varios ejemplos la multiplicación y división de números enteros, desde el caso en el que sólo intervienen dos números hasta cuando intervienen más.
- 00:00 a 06:38: Multiplicación y División simple de número enteros. (00:38 : Regla de los Signos.)
- 06:38 a 07:33: Ejercicios de Multiplicación y División simple.
- 07:33 a 12:30: Multiplicación y División compuesta de números enteros.
- 12:30 a 17:34: Ejercicios de Multiplicación y División compuesta.
Calcula:
Ejercicios sencillos de multiplicación y división de enteros.
Multiplicación y división:
Multiplicación y división de números enteros.
Introduce el resultado y cuando termines pulsa el botón "Corregir" de la parte inferior de la escena. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Ejercicios de autoevaluación sobre producto y cociente de números enteros.
En esta escena podrás practicar la multiplicación y división de números enteros.
Ejercicios de autoevaluación sobre multiplicaciones y divisiones de números enteros.
Ejercicios de autoevaluación sobre las propiedades del producto y del cociente de números enteros.
Suma, resta, multiplicación y división:
En esta escena podrás practicar la suma, resta, multiplicación y división de números enteros.
Operaciones combinadas con números enteros
A la hora de operar con números enteros utilizaremos la misma jerarquía de operaciones que con números naturales:
Ver: Jerarquía de las operaciones con números naturales
Jerarquía de las operaciones
A la hora de operar seguiremos las siguientes pautas:
- Primero se efectúan las operaciones del interior de los paréntesis. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
- Dentro de los paréntesis, o una vez quitados todos los paréntesis, las operaciones se efectúan en el siguiente orden:
- Las potencias y las raíces.
- Las multiplicaciones y las divisiones (de izquierda a derecha).
- Las sumas y las restas.
- Cuando aparecen paréntesis dentro de otros paréntesis, se puede optar por cambiar los paréntesis más exteriores por corchetes, con el fin de facilitar la lectura de la operación.
- Cuando resuelvas los paréntesis puedes completar las operaciones que encierren o aplicar la propiedad distributiva.
- En cada uno de los pasos que des para resolver una expresión con operaciones combinadas se puede llevar a cabo más de una operación, siempre que no suponga romper el orden que acabamos de establecer.
Tutorial en el que se explica a través de varios ejemplos el orden en el que hay que realizar las operaciones con números, lo que se llama la jerarquía de operaciones.
- 00:00 a 03:47 : Conceptos básicos. Jerarquía de operaciones.
- 03:47 a 19:37 : Ejercicios de Operaciones Combinadas.
Operaciones combinadas con enteros.
Efectúa:
a) 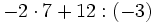
b) 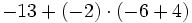
c) ![(-30):15-3 \cdot [(-3)+(-8)]\;](/wikipedia/images/math/e/6/8/e68cbfa29c5b2441d196f58e5650e229.png)
d) ![-2+4:[7+(-6):2]\;](/wikipedia/images/math/7/8/9/789c45348313c9a5a97d88770e651174.png)
e) 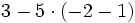
f) ![5+(-24):(+6)+5 \cdot [4-(-2) \cdot (+3)]\;](/wikipedia/images/math/3/2/e/32e813821a2ebe77944b02c2111bde3c.png)
Efectúa:
a) 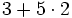
b) 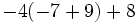
c) 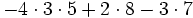
d) 
Efectúa:
a) 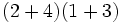
b) 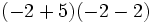
c) 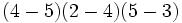
d) ![-2+[3+2(-3-1)]\;](/wikipedia/images/math/2/2/5/225a550a5c715d1274f269774c6cac8c.png)
e) ![-2{5-2[3-4+(1+2)-2(-1-1)]-3}+1\;](/wikipedia/images/math/f/1/7/f1746b8cc35742adcd78520262157f86.png)
Efectúa:
Efectúa:
a) 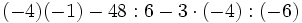
b) ![(-6):(+2)+[18-9:(+3)]\cdot (-2+4)+5 \cdot (-7)\;](/wikipedia/images/math/0/f/1/0f12794504f2a70e93d1f1a7d0f27e72.png)
Efectúa:
a) ![(-7)-\{9-[(-7)+(-13)-(-5)]+[23-(+18)+(-6)]\}\;](/wikipedia/images/math/8/5/f/85fda0cee7c9c7b7f463a471512b0756.png)
b) 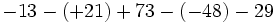
c) ![1-\{4-[-2+(5-1-9)-1]+2\}+3\;](/wikipedia/images/math/6/d/5/6d5616771a67c61c00a77f7b152ddae5.png)
Efectúa:
Efectúa:
Efectúa:
Efectúa:
Efectúa:
Efectúa:
Ejercicios resueltos de operaciones combinadas con números enteros.
En esta escena podrás practicar las operaciones con números enteros: suma, resta, multiplicación, cociente, potencia y raíz; con o sin paréntesis.
En esta escena podrás practicar las operaciones de suma, resta y multiplicación con paréntesis con 3 números enteros.
En esta escena podrás practicar las operaciones combinadas con paréntesis con 3 números enteros.
En esta escena podrás practicar las operaciones combinadas con paréntesis con 4 números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros con ayuda de la calculadora. (nivel 1)
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros con ayuda de la calculadora. (nivel 2)
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros. No incluye potencias ni raíces.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros. Incluye raíces y potencias.
Calculadora
Suma, resta, multiplicación y división
|
Calculadora: Suma, resta, multiplicación y división |
Opuesto
|
Calculadora: Opuesto |
Paréntesis
|
Calculadora: Paréntesis |
Potencias
|
Calculadora: Potencias |
Ejercicios y problemas
1) En las carreras de caballos un espectador apostó en 4 carreras y los resultados fueron estos: en la primera perdió 50 €;, en la segunda perdió 30 €; en la tercera ganó 40 € y en la cuarta ganó 600 €. ¿Cuál fue el balance total de sus apuestas?
2) La temperatura de una ciudad medida a las 7 de la mañana es de 4º sobre cero; de 7 a 10, la temperatura aumentó 5º; de 10 a 2 la temperatura aumentó 4º; de 2 a 5 no varió; de 5 a 9 descendió 3º y de 9 a 12 descendió 7º. ¿Cuál es la temperatura a las 12 de la noche?
3) A primeros de mes, Luis tenía en su cuenta 500 €. Al día siguiente ingresó 50 €. Al otro día sacó 200 € y a la semana siguiente sacó 100 €. El día 29 ingresó 250 € que le pagó un amigo. ¿Qué dinero le queda a final de mes?
4) Una sustancia que se encuentra a 50º pasa a 5º bajo cero. ¿Cuál es la variación de la temperatura?
5) La temperatura de una barra de hielo en un día de invierno es de 2º bajo cero. Se calienta y pasa a 50º sobre cero. ¿Cuál es la variación de temperatura?
6) En un juego, Luis ganó 12 cromos, después perdió 15 cromos, más tarde ganó 27 cromos y luego perdió 7 cromos. ¿Cuál fue el balance del juego?
7) Una sustancia que está a 11º bajo cero se calienta hasta ponerse a 11º sobre cero. ¿Cuál es la variación de temperatura?
8) Al construir un edificio de 10 plantas y 3 sótanos, el nivel de la calle donde está se considera altura cero; por encima, las alturas son positivas, y por debajo, negativas. calcula la distancia recorrida por un ascensor que va:
- de la altura -7 a la altura +25.
- de la altura -2 a la altura -8.
- de la altura +4 a la altura +15.
1) Una colección de libros de historia consta de 150 libros. El precio de los tres primeros juntos es de 32 euros, y el precio de los restantes hasta la mitad de la colección se vende a 25 euros cada libro. La segunda mitad de la colección se vende a 22 euros cada libro. ¿Cuál es el importe total de la colección?
2) Una isla tiene una superficie de 140 km2, y la densidad de población en esta isla (número de habitantes por km2) es de 250. La isla tiene 6 árboles por persona. ¿Cuál es el número aproximado de árboles de la isla?
3) En una bodega hay las siguientes cantidades de vino:
- 8 toneles con 10 000 litros cada uno.
- 15 toneles con 8 hl cada uno.
- 20 toneles con 6 hl cada uno.
Calcula el total de litros de vino que hay en la bodega.
Problemas de sumas y restas de enteros con o sin paréntesis.
Problemas resueltos con números enteros.
Problemas resueltos con números enteros.
Problemas resueltos con potencias y raíces de números enteros.
En esta escena podrás resolver problemas de compras en los que intervienen sumas, restas y multiplicaciones de números enteros.
|
Problemas: Operaciones con enteros
1. Estamos en la planta 345 de un gran rascacielos del futuro y bajamos en ascensor a la planta -15. ¿Cuánto tiempo tardaremos si el ascensor tarda 1 segundo en bajar 5 pisos?
Solución: 1' 12"
2. Pitágoras, filósofo y matemático griego, nació el año 582 a.C. y murió el año 496 a.C. ¿A qué edad murio? ¿Cuántos años han pasado hasta el año 2007 d.C. desde su muerte?
Solución:
3. Durante el ascenso a una montaña, la temperatura desciende 2 grados cada 200 m de ascenso. ¿A qué altura habrá que ascender para alcanzar -15ºC, si en el punto de partida, la temperatura es de 5ºC y este está a una altitud de 300 m?
Solución: 2.300 m. |
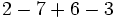
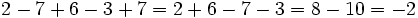
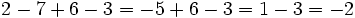
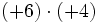
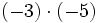
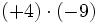
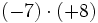
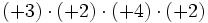
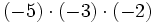
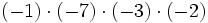
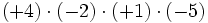
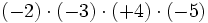
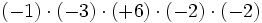
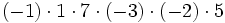
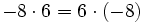
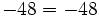
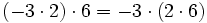
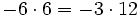
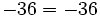
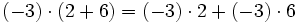
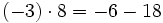
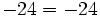
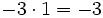
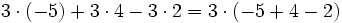
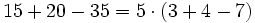
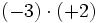
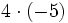
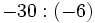
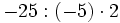
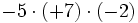
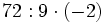
![-42 : [(-6) \cdot (-7)]\;](/wikipedia/images/math/9/7/b/97bf06a97f3e09f1e0dd13d3c5886e5a.png)
![[(+9) \cdot (-4)] : [-3 \cdot (+2)]\;](/wikipedia/images/math/0/8/5/0855f0174d3388d983075ce2f5995c46.png)
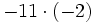
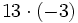
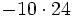
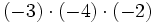

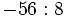
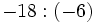
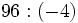
![[8-(-6)]:(+7)+(-9)\;](/wikipedia/images/math/d/7/d/d7d0b31fafbbbb0b156edb34e487cae3.png)
![18-(-2) \cdot[(+15):(8-11)]\;](/wikipedia/images/math/1/9/7/197dff4d42e5917261deea7756fe42d6.png)
![[8 + 6]:(+7)+(-9)\;](/wikipedia/images/math/8/4/e/84e6eb1dd9731dd92e13d5c09ecceff7.png)
![[14]:(+7)+(-9)\;](/wikipedia/images/math/b/8/5/b855f17314d0124a839a03b9c58ddfde.png)
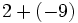
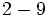
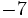
![18-(-2) \cdot[(+15):(-3)]\;](/wikipedia/images/math/b/f/f/bffdcd0011c95a2677f2441ab7af0bee.png)
![18-(-2) \cdot [-5]\;](/wikipedia/images/math/5/c/e/5cef9b8165c728c79e1c10031ec145c7.png)
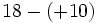
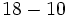
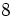
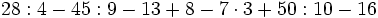
![8-\{7-[15-(6-9+1)-(3 \cdot 4-17)]\}-(-5+1)\;](/wikipedia/images/math/2/8/1/281c6dff8b881adee343ddf08db0c8ba.png)
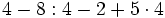
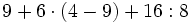
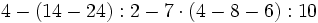
![25+40:(6-4)+[5-(8-9)]\;](/wikipedia/images/math/2/6/d/26d0311df03f52854ef572a315ff4fea.png)
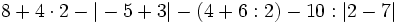
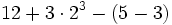
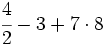


![(-3) \cdot [5 \cdot (8-6) -3 \cdot (3-7)]=](/wikipedia/images/math/f/5/9/f59deb2e37e79d7962fd952b00c1a69b.png)

