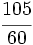Números racionales: Tipos de fracciones
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones I Fracciones II Fracciones III Números decimales | WIRIS Geogebra Calculadora Fracciones |
Tabla de contenidos |
Fracciones propias e impropias
¿Qué pasa si el numerador es mayor que el denominador? ¿Cómo se interpreta el hecho de tomar más partes de la unidad de las que que hay?
Vamos a dar respuesta a estas preguntas a continuación, pero primero necesitamos ver los conceptos de fracción propia e impropia.
- Fracciones propias son aquellas cuyo numerador (en valor absoluto) es menor que el denominador (en valor absoluto). Su valor absoluto es menor que 1.
- Fracciones impropias son aquellas que no son propias. Su valor absoluto es mayor que 1.
Representación gráfica de fracciones propias e impropias.
Actividad en la que debes separar las fracciones propias de las impropias
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Las fracciones impropias representan algo mayor que el todo, es decir, cuando trabajamos con una fracción impropia damos a entender que tenemos unidades completas de algo y, posiblemente, alguna unidad incompleta.
Esto queda de manifiesto en la proposición y en los ejemplos que damos a continuación.
Proposición Toda fracción impropia, 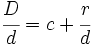
donde Demostración:
|
Ejemplo 1:
La fracción 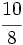 es impropia.
es impropia.
Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 4):
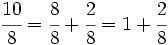
Ejemplo 2:
La frácción 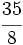 es impropia. La podemos decomponer en la suma de un entero y una fracción propia.
es impropia. La podemos decomponer en la suma de un entero y una fracción propia.
Para ello, dividimos 35 entre 8:
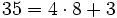
El dividendo 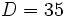 , el divisor
, el divisor 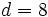 , el cociente
, el cociente 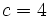 y el resto
y el resto 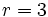 .
.
Aplicando la proposición anterior:
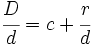
y sustituyendo cada letra por su valor:
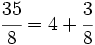
Actividades sobre el signo de las fracciones y sobre la descomposición de fracciones impropias como suma de un entero y una fracción propia.
Números mixtos
Una fracción mixta o número mixto es la representación de una fracción impropia como un número entero más una fracción propia, en la que se omite el signo de suma.
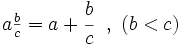
La fracción situada a la derecha del entero suele escribirse con una tipografía de menor tamaño para que no se confunda con una multiplicación de un número por una fracción.
Números mixtos. Ejemplos de paso de forma fraccionaria a mixta y viceversa.
Conversión de fracción impropia a número mixto
Conversión de fracción impropia a número mixto.
Conversión de fracción impropia a número mixto.
Escribiendo una fracción impropia com un número mixto
Convierte a número mixto la siguiente fracción impropia: 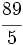
Nota: En el video, la división está realizada por el método anglosajón
Convierte a número mixto la siguiente fracción impropia: 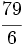
Nota: En el video, la división está realizada por el método anglosajón
Conversión de número mixto a fracción impropia
Conversión de número mixto a fracción impropia.
Conversión de número mixto a fracción impropia.
Convierte a fracción impropia el siguiente número mixto: 
Nota: En el video, la división está realizada por el método anglosajón
Convierte a fracción impropia el siguiente número mixto: 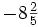
Nota: En el video, la división está realizada por el método anglosajón
Números mixtos y fracciones impropias.
Actividades de nivel variable en las que deberás obtener la forma mixta de una fracción.
|
Calculadora: Fracciones mixtas |
Fracciones equivalentes
Fracciones equivalentes
| El siguiente videotutorial condensa todo lo que se va a ver en este tema sobre fracciones equivalentes:
Tutorial que explica el concepto de fracciones equivalentes y como obtener la fracción irreducible a una dada.
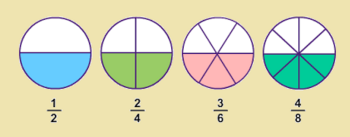
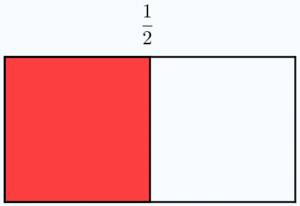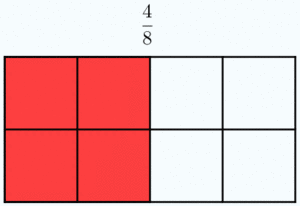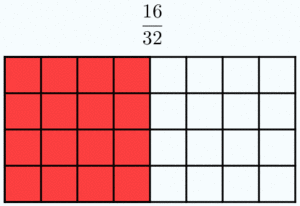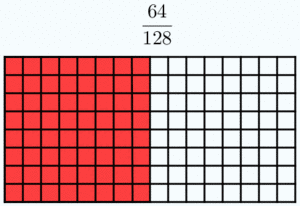
Dos fracciones son equivalentes si tienen el mismo valor. En la Fig.1 tienes ejemplos de fracciones equivalentes. Fíjate como representan la misma porción de la unidad aunque sus numeradores y denominadores sean diferentes.
Introducción a fracciones equivalentes. Modelos de fracciones equivalentes. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe las fracciones que representen cada uno de los puntos representados en la recta numérica. ¿Qué puedes decir de esas fracciones? Escribe las fracciones que representen cada uno de los puntos representados en la recta numérica. ¿Qué puedes decir de esas fracciones? Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Calcula cuatro fracciones equivalentes a Calcula cuatro fracciones que representen al número racional |
Obtención de fracciones equivalentes
| Piensa un número. Multiplícalo por 2. Divide el resultado entre 2. ¿Qué sucede?. Lógicamente, el número vuelve a ser el que era al principio porque la multiplicación y la división son operaciones inversas.
Esta idea, junto al hecho de que las fracciones sean el cociente de dos números enteros, permite que muchas fracciones representen el mismo número racional. Más que muchas, infinitas. Piensa, por ejemplo, en la fracción 1/2. Si multiplicamos su numerador y su denominador por el mismo número entero distinto de cero, en realidad, no estamos variando el valor de la fracción. Gráficamente, multiplicar el numerador y el denominador de una fracción por el mismo número significa partir el "todo" que estamos considerando en piezas más pequeñas, pero en realidad no varía la cantidad de ese "todo" que se toma. Fíjate en la animación para entenderlo mejor. |
Obtención de fracciones equivalentes
Si se multiplica o se divide (de forma exacta) el numerador y el denominador de una fracción por un mismo número distinto de cero, se obtiene una fracción equivalente. Si además el número por el que multiplicamos o dividimos es distinto de 1, estos procedimientos reciben el nombre de amplificación y simplificación, respectivamente.
En realidad, estos dos procesos son inversos el uno del otro. La única diferencia importante entre uno y otro es que, mientras la amplificación se puede hacer siempre, la simplificación sólo es posible si el numerador y el denominador tienen un divisor común mayor que 1.
Amplificación
| Simplificación
|
Obtención de fracciones equivalentes: por amplificación y por simplificación.
Obteniendo fracciones equivalentes por simplificación.
Obteniendo fracciones equivalentes por amplificación y simplificación.
Obtén dos fracciones equivalentes a 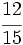 : una por amplificación y otra por simplificación.
: una por amplificación y otra por simplificación.
Escribe tres fracciones equivalentes a 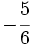 por amplificación.
por amplificación.
Escribe tres fracciones equivalentes a 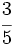 por amplificación.
por amplificación.
Escribe tres fracciones equivalentes a 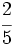 por amplificación.
por amplificación.
Escribe dos fracciones equivalentes a 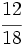 por amplificación.
por amplificación.
Halla una fracción equivalente a 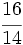 por amplificación y otra por simplificación.
por amplificación y otra por simplificación.
Escribe dos fracciones equivalentes a 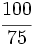 por simplificación.
por simplificación.
Escribe dos fracciones equivalentes a 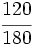 por simplificación.
por simplificación.
Escribe tres fracciones equivalentes a 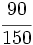 por simplificación.
por simplificación.
Busca una fracción equivalente a la dada con la ayuda del gráfico.
- a) Escribe una fracción equivalente a la dada.
- b) Empareja las fracciones equivalentes.
Fracciones equivalentes. Representación en la recta numérica.
Encontrar fracciones equivalentes por medio de la multiplicación.
Completa la fracción para que se cumpla la igualdad.
Completa la fracción para que se cumpla la igualdad.
Completa la fracción para que se cumpla la igualdad.
Encontrar fracciones equivalentes por medio de la multiplicación.
Simplificación de fracciones
- Simplificar una fracción es sustituirla por otra equivalente con el numerador y denominador menores que los de partida.
- Cuando una fracción no se puede simplificar se dice que es irreducible.
Procedimiento: Simplificación
- Para simplificar fracciones se divide numerador y denominador por un mismo número, distinto de 0 y 1. Este proceso se puede repetir hasta hacer la fracción irreducible.
- Si queremos hacer la fracción irreducible en un solo paso debemos dividir numerador y denominador por el m.c.d. de ambos.
Simplifica 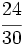 :
:
Solución:
- Paso a paso: Dividimos por 2 y luego por 3
- En un solo paso: Calculamos el m.c.d.(24,30) = 6, y dividimos directamente por 6:
Simplificación de fracciones (3 métodos). Fracción irreducible. Ejemplos.
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: | Simplifica: Simplifica: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: |
- Actividades en las que deberás simplificar fracciones con o sin ayuda.
- Actividad en la que debes emparejar cada fracción con su irreducible.
Actividad en las que deberás encontrar la fracción irreducible.
Actividades de nivel variable en las que deberás simplificar fracciones.
Simplifica fracciones.
La simplificación de fracciones me proporciona un método para saber si dos fracciones son equivalentes.
Procedimiento
Si al simplificar dos fracciones se obtiene la misma fracción irreducible, entonces las dos fracciones son equivalentes.
Determina si 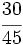 y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
son fracciones equivalentes.
Simplificar fracciones. Fracciones irreducibles
Simplificar una fracción consiste en obtener otra fracción equivalente con numerador y denominador menores. Para ello debemos dividir numerador y denominador por un mismo número. Este proceso se puede repetir hasta que ya no encontremos más divisores comunes distintos de 1, en cuyo caso, la fracción obtenida se dice que es irreducible.
|
Actividades Interactivas: Simplificación de fracciones
Actividad 1: Simplifica las fracciones.
Actividad: Todas las fracciones equivalentes entre sí representan el mismo número racional. Por tanto, para expresar un mismo valor nos interesa emplear la fracción más simple, ésa será la que tenga el numerador y denominador más pequeños. A esa fracción se la llama fracción irreducible porque ya no se la puede simplificar más. Nos valemos de la propiedad fundamental de la división. Sabemos que si multiplicamos o dividimos al numerador y al denominador por el mismo número obtenemos otra fracción equivalente. Para simplificar una fracción debemos buscar un número que sea divisor del numerador y del denominador para dividirlos por él. Nos interesa dividirlos por el número mayor posible, ese número es el máximo común divisor de ambos, así, de una sola vez habremos llegado a la fracción irreducible.
En esta escena aparece aleatoriamente una fracción, además se indican los divisores comunes del numerador y del denominador. Abajo debes marcar el número por el que dividirías al numerador y denominador para simplificar esa fracción. Pulsa "inicio" para que aparezca otra fracción.
Esta actividad es semejante a la anterior, pero en ésta no se da ayuda. Busca un número por el que puedes simplificar esta fracción, márcalo abajo y pulsa intro. Te indicará si con ello has llagado a la fracción irreducible o si todavía puedes seguir simplificando. En ese caso marca otro número. Tienes tres intentos para llegar a la fracción irreducible, pero no puedes rectificar, por eso no utilices los triángulos para cambiar los números marcados. Si la primera fracción es ya irreducible, marca el 1. Pulsa "inicio" para que aparezca otra fracción.
Actividad 2: Coloca junto a cada fracción su fracción irreducible.
Actividad:
Las fracciones de abajo son las irreducibles de las fracciones de arriba. Colócalas juntas. Pulsa "inicio" para que aparezcan otras fracciones.
Esta actividad es semejante a la anterior, empleando números de hasta dos cifras. Pulsa "inicio" para que aparezcan otras fracciones.
Esta actividad es semejante a la anterior, empleando números de hasta tres cifras. Pulsa "inicio" para que aparezcan otras fracciones. |
Ejercicios
|
Ejercicios: Tipos de fracciones 1. Agrupa las fracciones que sean equivalentes: Solución: 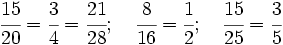 2. Simplifica las fracciones:
Solución: a) 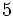 b) b) 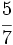 c) c) 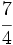 |
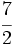 es una fracción impropia porque 7 > 2.
es una fracción impropia porque 7 > 2.
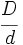 , se puede escribir como suma de un número entero y una fracción propia.
, se puede escribir como suma de un número entero y una fracción propia.
 es el cociente y
es el cociente y  es el resto de la división de
es el resto de la división de  entre
entre  .
.
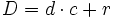
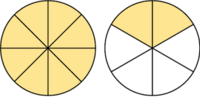
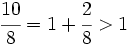
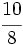 de la Fig. 4 hemos visto que se puede expresar mediante el número mixto
de la Fig. 4 hemos visto que se puede expresar mediante el número mixto 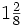 :
:
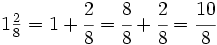
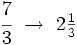 ; B)
; B) 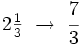
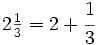
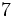

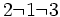 ; B)
; B) 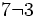
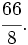
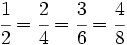
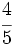 y
y 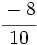 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
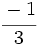 y
y 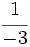 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
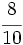 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
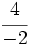 y
y 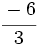 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
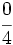 y
y 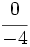 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
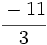 y
y 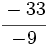 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
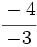 y
y 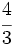 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
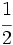 y represéntalas en la recta numérica. ¿Qué observas?
y represéntalas en la recta numérica. ¿Qué observas?
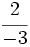 y represéntalas en la recta numérica.
y represéntalas en la recta numérica.
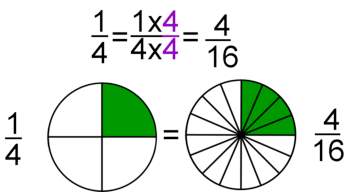
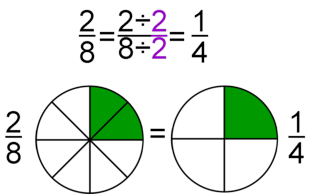
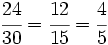
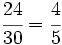
 b)
b) 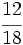
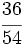 b)
b) 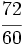
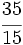 b)
b) 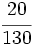
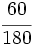 b)
b) 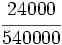
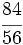 b)
b) 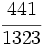
 b)
b) 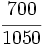
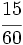
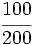 .
.
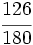 .
.
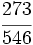 .
.
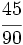 .
.
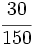 .
.
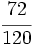 .
.
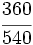 .
.
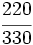 .
.
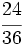 .
.
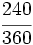 .
.
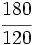 .
.
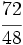 .
.
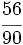 .
.
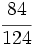 .
.
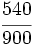 .
.
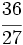 .
.
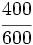 .
.
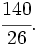
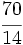 b)
b)  c)
c)