Problemas de proporcionalidad (3ºESO Académicas)
De Wikipedia
| Revisión de 18:43 13 sep 2016 Coordinador (Discusión | contribuciones) (→Proporcionalidad simple inversa) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Proporcionalidad simple directa) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| __TOC__ | __TOC__ | ||
| + | {{p}} | ||
| + | ==Introducción== | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Proporciones numéricas | ||
| + | |duracion=14'16" | ||
| + | |sinopsis=Tutorial en el que se explica y trabaja la proporción numérica, la razón de proporción, y cuando cuatro números guardan proporción. - | ||
| + | *00:00 a 02:40: Introducción (ejemplos). | ||
| + | *02:40 a 03:15: Definición de razón de proporción entre dos cantidades (números). | ||
| + | *03:15 a 05:24: Ejemplos 1-2-3 de razón de proporción entre dos números. | ||
| + | *05:24 a 08:15: Ejemplo 4 de aplicación de razón. | ||
| + | *08:15 a 09:40: Definición de cuándo cuatro números guardan proporción. Producto de medios y producto de extremos. - 09:40 a 12:20: Ejemplos 5-6-7 de razón de proporción entre dos números. - 12:20 a Fin: Ejemplo 8 de aplicación de razón. | ||
| + | |url1=https://www.youtube.com/watch?v=u-u6UmOzL8o&index=1&list=PLZNmE9BEzVIkOdmbGm3jJH7F7sf1hpvYa | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| (Pág. 44) | (Pág. 44) | ||
| - | ==Proporcionalidad simple== | + | ==Proporcionalidad simple directa== |
| - | ===Proporcionalidad simple directa=== | + | {{Regla de tres directa}} |
| + | {{AI_cidead | ||
| + | |titulo1=Regla de tres simple directa (II) | ||
| + | |descripcion=Actividades para aprender y practicar la regla de tres simple directa. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena4/2quincena4_contenidos_2b.htm | ||
| + | }} | ||
| + | {{p}} | ||
| + | ===Ejercicios y problemas=== | ||
| {{Ejemplo | {{Ejemplo | ||
| |titulo=Ejercicio resuelto: ''Proporcionalidad simple directa'' | |titulo=Ejercicio resuelto: ''Proporcionalidad simple directa'' | ||
| |enunciado={{p}} | |enunciado={{p}} | ||
| - | :Para transportar 120000 l de agua, se necesitan 8 camiones cisterna. ¿Cuántos camiones se necesitarán para transportar 315000 l? | + | Para transportar 120000 l de agua, se necesitan 8 camiones cisterna. ¿Cuántos camiones se necesitarán para transportar 315000 l? |
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| - | A más volumen de agua a transportar, más camiones se necsitarán. Las magnitudes "volumen de agua" y "nº de camiones" son directamente proporcionales: | + | A más volumen de agua a transportar, más camiones se necesitarán. Las magnitudes "volumen de agua" y "nº de camiones" son directamente proporcionales: |
| + | |||
| {{Tabla50|celda1= | {{Tabla50|celda1= | ||
| Regla de tres simple directa: | Regla de tres simple directa: | ||
| Línea 26: | Línea 47: | ||
| |celda2= | |celda2= | ||
| - | {{b4}}<math>x=\frac{315000 \cdot 8}{120000}= 21</math> camiones | + | {{b4}}<math>x=\frac{315\,000 \cdot 8}{120\,000}= 21</math> camiones |
| }} | }} | ||
| }} | }} | ||
| + | {{Actividades y videotutoriales: Regla de tres directa}}{{p}} | ||
| {{p}} | {{p}} | ||
| - | ===Proporcionalidad simple inversa=== | + | ==Proporcionalidad simple inversa== |
| + | {{Regla de tres inversa}} | ||
| + | {{p}} | ||
| + | |||
| + | ===Actividades y videotutoriales=== | ||
| {{Ejemplo | {{Ejemplo | ||
| |titulo=Ejercicio resuelto: ''Proporcionalidad simple inversa'' | |titulo=Ejercicio resuelto: ''Proporcionalidad simple inversa'' | ||
| |enunciado={{p}} | |enunciado={{p}} | ||
| - | :6 pintores tardan 8 días en pintar una casa. ¿Cuánto tardarán 4 pintores en realizar la misma tarea? | + | 6 pintores tardan 8 días en pintar una casa. ¿Cuánto tardarán 4 pintores en realizar la misma tarea? |
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| A menos pintores, más días tardarán en hacer la misma tarea. Las magnitudes "nº de pintores" y "tiempo" son inversamente proporcionales: | A menos pintores, más días tardarán en hacer la misma tarea. Las magnitudes "nº de pintores" y "tiempo" son inversamente proporcionales: | ||
| {{Tabla50|celda1= | {{Tabla50|celda1= | ||
| - | Regla de tres simple directa: | + | Regla de tres simple inversa: |
| nº pintores tiempo (días) | nº pintores tiempo (días) | ||
| Línea 52: | Línea 78: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Actividades y videotutoriales: Regla de tres inversa}} | ||
| + | {{p}} | ||
| + | |||
| (Pág. 45) | (Pág. 45) | ||
| ==Proporcionalidad compuesta== | ==Proporcionalidad compuesta== | ||
| - | {{Ejemplo | + | {{Proporcionalidad compuesta}} |
| - | |titulo=Ejercicio resuelto: ''Proporcionalidad compuesta'' | + | |
| - | |enunciado= | + | |
| - | {{p}} | + | |
| - | |sol=}} | + | |
| {{p}} | {{p}} | ||
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
| {{ejercicio | {{ejercicio | ||
| - | |titulo=Ejercicios propuestos: ''Proporcinalidad'' | + | |titulo=Ejercicios propuestos: ''Proporcionalidad'' |
| |cuerpo= | |cuerpo= | ||
| {{b4}}(Pág. 46) | {{b4}}(Pág. 46) | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Introducción
Tutorial en el que se explica y trabaja la proporción numérica, la razón de proporción, y cuando cuatro números guardan proporción. -
- 00:00 a 02:40: Introducción (ejemplos).
- 02:40 a 03:15: Definición de razón de proporción entre dos cantidades (números).
- 03:15 a 05:24: Ejemplos 1-2-3 de razón de proporción entre dos números.
- 05:24 a 08:15: Ejemplo 4 de aplicación de razón.
- 08:15 a 09:40: Definición de cuándo cuatro números guardan proporción. Producto de medios y producto de extremos. - 09:40 a 12:20: Ejemplos 5-6-7 de razón de proporción entre dos números. - 12:20 a Fin: Ejemplo 8 de aplicación de razón.
(Pág. 44)
Proporcionalidad simple directa
Procedimiento
La regla de tres directa es un método que se apoya en el hecho de que al dividir dos magnitudes directamente proporcionales el cociente no varía. Esto permite establecer una igualdad entre dos fracciones, de la cual se despeja el valor desconocido.
Compramos 4 kg de plátanos por 6 €. ¿Cuánto costarán 7 kg?
Solución:
Peso (kg) Coste (€)
---------- ----------
4 --------> 6
7 --------> x
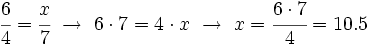 €
€
Una paleta de jamón de 4 kg cuesta40 €. ¿Cuánto costará otra paleta de igual calidad de 5 kg?
En un día de trabajo de 8 horas, un obrero ha hecho 10 cajas. ¿Cuántas horas tardará en hacer 25 cajas similares?
Actividades para aprender y practicar la regla de tres simple directa.
Actividades para aprender y practicar la regla de tres simple directa.
Por 3 horas trabajando he ganado 60 €. ¿Cuánto ganaré por 8 horas?
600 gramos de queso cuestan 12 €. ¿Cuánto gramos podré comprar con 4.50 €?
Problemas de regla de tres.
Actividades para aprender y practicar la regla de tres simple directa.
Ejercicios y problemas
Ejercicio resuelto: Proporcionalidad simple directa
Para transportar 120000 l de agua, se necesitan 8 camiones cisterna. ¿Cuántos camiones se necesitarán para transportar 315000 l?
A más volumen de agua a transportar, más camiones se necesitarán. Las magnitudes "volumen de agua" y "nº de camiones" son directamente proporcionales:
Regla de tres simple directa:
Volumen (l) nº camiones
---------- D -----------
120000 ------> 8
315000 ------> x
| 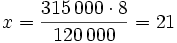 camiones camiones
|
Tutorial que explica los problemas de proporcionalidad directa, viendo los métodos de igualdad de cocientes, método general, reducción a la unidad y regla de tres directa.
Problemas de proporcionalidad directa:
- Me han dado 4.20 € como paga de los últimos 7 días. ¿Cuánto me darán por 15 días?
- A una fábrica de muebles han llegado 840 camiones de madera en 60 días. Si el flujo de camiones se mantiene, ¿cuántos camiones recibirá en un año?
- Hemos tardado 2 horas y media en recorrer un trayecto de 125 km. Si seguimos a la misma velocidad constante, ¿cuánto tiempo tardaremos si la ruta de regreso es de 225 km?
Tutorial que explica el concepto de magnitudes directamente proporcionales.
Tutorial que explica los problemas de proporcionalidad directa.
Se necesitan 70 galones de pintura para embellecer 5 casas de un condominio. ¿Que cantidad de pintura se requiere para 12 casas similares?
Si una máquina copiadora tarda 8 segundos en sacar 20 copias, ¿cuánto tiempo tardará en sacar 45 copias?
Plantea la proporción sin resolverla:
- a) 9 marcadores cuestan $115. ¿Cuánto cuestan 7 marcadores?
- b) 7 manzanas cuestan %50. ¿Cuántas manzanas puedo comprar por $80?
- c) Una receta de pastel para 5 personas requiere 2 huevos. ¿Cuántos huevos requiere la misma receta para 15 personas?
Mica puede comer 21 tacos en 66 minutos. Ella quiere saber cuántos minutos tardará en comer 35 tacos si puede mantener el mismo ritmo.
Una receta para galletas de avena contiene 2 tazas de harina por cada 3 tazas de avena. ¿Cuánta harina se necesita para elaborar una gran cantidad de galletas que requieren 9 tazas de avena?
Tu carro puede recorrer 25 millas por galón de combustible, y quieres hacer un viaje de 400 millas. Justo ahora la gasolina cuesta 30 pesos por galón. ¿Cuánto te va a acostar la gasolina para el vaije?
Practica distintos problemas de proporcionalidad directa.
Practica distintos problemas de proporcionalidad directa.
Problemas de regla de tres simple directa con pistas.
Tasas.
Actividades para practicar la regla de tres simple directa.
Actividades para practicar la regla de tres simple directa.
Actividades para practicar la regla de tres simple directa.
Escribir proporciones.
Problemas verbales de proporciones.
Problemas verbales de varias unidades.
Problemas de autoevaluación sobre la regla de tres simple directa.
Ejercicios y problemas de autoevaluación sobre proporcionalidad directa.
Tasas unitarias.
Problemas de tasas.
Comparar tasas.
Proporcionalidad simple inversa
Procedimiento
La regla de tres inversa es un método que se apoya en el hecho de que al multiplicar dos magnitudes directamente proporcionales el producto no varía. Esto permite establecer una ecuación de la cual se obtiene el valor desconocido.
Dos grifos tardan en llenar una piscina en 6 horas. ¿Cuánto tiempo taradarán 3 grifos?
Solución:
Nº grifos Tiempo (h)
--------- ----------
2 --------> 6
3 --------> x
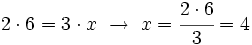 h
h
Actividades para que aprendas y practiques la regla de tres inversa.
Actividades y videotutoriales
Ejercicio resuelto: Proporcionalidad simple inversa
6 pintores tardan 8 días en pintar una casa. ¿Cuánto tardarán 4 pintores en realizar la misma tarea?
A menos pintores, más días tardarán en hacer la misma tarea. Las magnitudes "nº de pintores" y "tiempo" son inversamente proporcionales:
Regla de tres simple inversa:
nº pintores tiempo (días)
----------- I ------------
6 ------> 8
4 ------> x
| 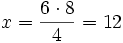 días días
|
Tutorial que explica los problemas de proporcionalidad inversa, viendo los métodos de igualdad de productos, método general, reducción a la unidad y regla de tres inversa.
Problemas de proporcionalidad inversa:
- Manuel ha hecho la mudanza de su casa en 6 viajes, utilizando para ello su coche, en el que caben 300 kg. ¿Cuántos viajes haría si hubiese alquilado una furgoneta con capacidad para 360 kg?
- Un ciclista que viaja a 22 km/h tarda 45 min en cubrir la contrareloj del día. ¿Cuánto tardaría si fuera a 33 km/h?
- Necesitamos 15 obreros para levantar un muro en 1 hora. ¿Cuántos obreros se necesitan para levantarlo en tres cuartos de hora?. ¿Y para levantarlo en 20 min?
Tutorial que explica los problemas de proporcionalidad inversa.
Tutorial que explica los problemas de proporcionalidad inversa.
Si 25 jardineros tardan 12 días en podar los árboles de un parque, ¿cuántos jardineros harán falta para realizar el mismo trabajo en 10 días?
Toma 20 min en llenar un tanque con un grifo que tiene un caudal de 20 litros/seg. Si se utiliza un grifo que arroja 9 litros/seg más que el anterior, ¿en cuánto tiempo se llenará el tanque?
Practica distintos problemas de proporcionalidad inversa.
Resuelve problemas de regla de tres simple inversa.
Problemas de autoevaluación sobre la regla de tres simple inversa.
Ejercicios y problemas de autoevaluación sobre proporcionalidad inversa.
Resuelve problemas de regla de tres simple. Tendrás que averiguar si son directas o inversas.
(Pág. 45)
Proporcionalidad compuesta
Cuando se trabaja con más de dos magnitudes ligadas por la relación de proporcionalidad (directa y/o inversa) diremos que nos encontramos frente a una situación de proporcionalidad compuesta.
Ejemplos sobre proporcionalidad compuesta.
Ejercicio resuelto: Proporcionalidad compuesta
Un solador embaldosa 260 m2 de suelo en 5 días trabajando 8 horas diarias. Se compromete a embaldosar un suelo de 500 m2 en 7 días. ¿Cuántas horas diarias tiene que trabajar?
Método rápido:
| Tenemos tres variables: Superficie, número de días y numero de horas diarias.
Si fijamos la superficie, a máyor número de días, menor número de horas de trabajo diarias: La proporcionalidad es inversa. Si fijamos el número de días, a mayor superficie, mayor número de horas de trabajo diarias: La proporcionalidad es directa. Superficie (m2) Nº de días Nº horas diarias
-------------- ----------- I -----------------
260 ------> 5 ------> 8
500 ------> 7 ------> x
└---------------------------------------┘
D
| 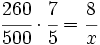
|
Método paso a paso:
Fijo la superficie en 260 m2:
Superficie (m2) Nº de días Nº horas diarias
-------------- ----------- I -----------------
260 ------> 5 ------> 8
260 ------> 7 ------> y
| 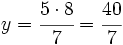 días. días.
|
Fijo los días en 7:
Superficie (m2) Nº de días Nº horas diarias
-------------- ----------- I -----------------
260 ------> 7 ------> 40/7
500 ------> 7 ------> x
└---------------------------------------┘
D
| 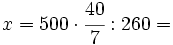
|
Tutorial que explica los problemas de proporcionalidad compuesta (directa e inversa), viendo distintos métodos para dar con la solución.
Tutorial que explica los problemas de proporcionalidad compuesta.
Ejemplos de problemas de proporcionalidad compuesta.
Tutorial que explica los problemas de proporcionalidad compuesta por reducción a la unidad.
Ejemplos de problemas de proporcionalidad compuesta por reducción a la unidad.
Para cortar el césped de un campo de futbol de 4500 m2 precisamos 3 operarios trabajando durante hora y media. ¿Cuántos operarios precisaremos otro día si queremos cortar el césped de otro campo de 6000 m2 y contamos con 2 horas para hacer el trabajo?
Problema.
Practica con distintas situaciones de proporcionalidad compuesta.
Practica con problemas de proporcionalidad compuesta de varios tipos.
Problemas de autoevaluación sobre proporcionalidad compuesta.
Problemas de autoevaluación sobre proporcionalidad compuesta.
Ejercicios propuestos
|
Ejercicios propuestos: Proporcionalidad |
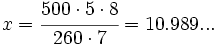
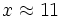 horas diarias.
horas diarias.
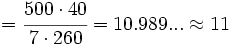 horas diarias.
horas diarias.

