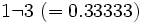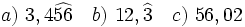Paso de decimal a fracción (3ºESO Académicas)
De Wikipedia
| Revisión de 11:13 19 oct 2017 Coordinador (Discusión | contribuciones) (→Paso de decimal a fracción) ← Ir a diferencia anterior |
Revisión de 11:17 19 oct 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| (Pág. 18) | (Pág. 18) | ||
| ==Paso de decimal a fracción== | ==Paso de decimal a fracción== | ||
| - | {{Paso de decimal a fracción}} | + | {{Fracción generatriz}} |
| {{p}} | {{p}} | ||
| - | |||
| ==Números con infinitos decimales no periódicos== | ==Números con infinitos decimales no periódicos== | ||
| Los números decimales con infinitas cifras no periódicas no pueden ponerse en forma de fracción. Por tanto, no son racionales. Como por ejemplo: | Los números decimales con infinitas cifras no periódicas no pueden ponerse en forma de fracción. Por tanto, no son racionales. Como por ejemplo: | ||
Revisión de 11:17 19 oct 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 18)
Paso de decimal a fracción
Se llama fracción generatriz de un número decimal, a aquella que tiene como valor dicho número decimal.
Toda fracción se puede pasar a forma decimal, sin embargo, lo contrario no es cierto: sólo se pueden pasar a fracción aquellos decimales que sean exactos o periódicos. Cuando el número de decimales es infinito y no periódico (número irracional), como ocurre con el número pi (π), no podemos expresarlo en forma de fracción.
- Actividad en la que podrás ver como se obtiene la fracción generatriz de una expresión decimal exacta, periódica pura o periódica mixta.
- Actividad en la que tendrás que hallar la fracción generatriz de una expresión decimal.
Cómo obtener la fracción generatiz de un número decimal exacto o periódico (2 métodos) con ejemplos:
1. a) 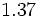 b)
b) 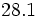 c)
c) 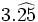 d)
d) 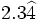
2. a) 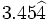 b)
b) 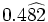 c)
c) 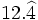
Tutorial en el que se da un rápido repaso a los distintos tipos de decimales y se explica el paso de un número en expresión decimal a su expresión fraccionaria equivalente, tanto en el caso de decimales finitos como periódicos.
Paso de decimal exacto a fracción
La fracción generatriz de un decimal exacto tiene en el numerador la expresión decimal sin la coma, y en el denominador un uno seguido de tantos ceros como cifras decimales.
Es el caso más sencillo. Estos decimales tienen un número finito de cifras decimales. Sólo tenemos que "mover" la coma a la derecha tantos puestos como sea necesario. Para "mover" la coma basta con multiplicar por una potencia de 10. Si queremos mover un puesto, multiplicamos por 10, si son dos puestos, por 100, tres puestos, por 1000... Pero no podemos simplemente multiplicar, porque así cambiaría el valor del número. Hay que "compensar" esa multiplicación con su operación opuesta, la división. Lo que hacemos es poner como denominador la misma potencia de 10 por la que hemos multiplicado el número. Después sólo quedaría simplificar la fracción
También podemos proceder siguiendo el siguiente algoritmo:
- Sea N el número decimal exacto cuya fracción generatriz queremos hallar.
- Multiplicamos N por 10 elevado al número de decimales.
- Despejamos N para obtener la fracción.
Paso de decimal exacto a fracción y su simplificación.
Cómo obtener la fracción generatiz de un número decimal exacto. Ejemplos.
Halla la fracción generatriz de 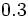
Halla la fracción generatriz de 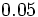
Halla la fracción generatriz de 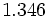
Halla la fracción generatriz de los números:
- a)
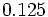
- b)
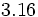
Halla la fracción generatriz de los números:
- a)
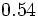 ; b)
; b) 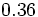 ; c)
; c) 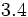 ; d)
; d) 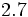 ; e)
; e) 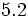 ; f)
; f) 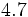 ; g)
; g) 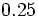 ; h)
; h) 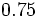 ; i)
; i) 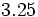 ; j)
; j) 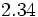 ; k)
; k) 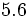 ; l)
; l) 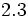 ;
;
Transforma en fracción los siguientes números decimales exactos:
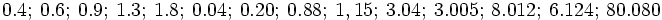
Halla la fracción generatriz de 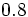
Halla la fracción generatriz de 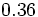
Halla la fracción generatriz de 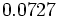
Halla la fracción generatriz de 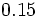
Convierte en número mixto 
Actividad en la que debes pasar de decimal exacto a fracción.
Paso de decimal periódico puro a fracción
La fracción generatriz de un número decimal periódico puro tiene como numerador la diferencia entre a y b, donde a es el número escrito sin la coma (sin repetir el periodo) y b es la parte entera del número; y como denominador, tantos "9" como cifras tiene el periodo.
Este caso es un poco más complicado. Como estos números tienen infinitas cifras decimales, no podemos simplemente "mover" la coma. La idea es buscar otro decimal con el mismo período a partir del decimal que tenemos. Una vez hecho esto, restaremos esos decimales con idéntico período, de forma que el resultado sea un entero. La única "pega" es que tendremos que resolver una pequeña ecuación.
El algoritmo es el siguiente:
- Sea N el número decimal cuya fracción generatriz queremos hallar.
- Multiplicamos N por 10 elevado al número de cifras que tenga el periodo, lo que permite obtener otro número con la misma parte decimal.
- Restamos N y el número obtenido en el paso anterior.
- Despejando N llegamos a la fracción buscada.
Halla la fracción generatriz de los números periódicos puros (2 métodos):
- a) 1.6666...
- b) 2.646464...
Halla la fracción generatriz de número periódico puro 0.3636... (Método largo)
Halla la fracción generatriz de los siguientes números periódicos puros (Método corto):
- a) 0.888...
- b) 0.212121...
- c) 0.537537537...
- d) 2.444...
- e) 10.484848...
Halla la fracción generatriz de los números (Método corto):
- a) 0.363636...
- b) 2.045045...
Halla la fracción generatriz de 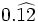 (Método corto)
(Método corto)
Halla la fracción generatriz de 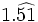 (Método corto)
(Método corto)
Halla la fracción generatriz de 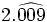 (Método corto)
(Método corto)
Halla la fracción generatriz por el método corto de:
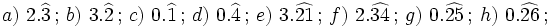
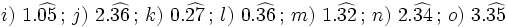
Actividad en la que debes pasar de decimal periódico puro a fracción.
Paso de decimal periódico mixto a fracción
La fracción generatriz de un número decimal periódico mixto tiene como numerador la diferencia entre a y b, donde a es el número escrito sin la coma (sin repetir el periodo) y b es el número escrito sin la coma quitándole la parte decimal periódica. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras tenga el anteperiodo.
Este caso es aún más complicado. La idea es buscar dos decimales con el mismo período a partir del decimal que tenemos. Una vez hecho esto, restaremos esos decimales con idéntico período, de forma que el resultado sea un entero. La única "pega" es que tendremos que resolver una pequeña ecuación.
El algoritmo es el siguiente:
- Sea N el número decimal cuya fracción generatriz queremos hallar.
- Multiplicamos N por 10 elevado al número de cifras que tenga el periodo más el anteperiodo.
- Multiplicamos N por 10 elevado al número de cifras que tenga el anteperiodo, lo que permite obtener otro número con la misma parte decimal que el del paso 2.
- Restamos los números obtenidos en los pasos 2 y 3.
- Despejando N llegamos a la fracción buscada.
Halla la fracción generatriz de los siguientes números periódicos mixtos (2 métodos):
- a) 2.46666...
- b) 3.246262626...
Halla la fracción generatriz de número periódico mixto 0.4333... (Método largo)
Halla la fracción generatriz de los siguientes números periódicos mixtos (Método corto):
- a) 0.5111...
- b) 0.935555...
- c) 3.8121212...
- d) 1.06434343...
Halla la fracción generatriz de los siguientes números periódicos mixtos (Método corto):
- a) 0.3851851...
- b) 4.1244444...
Halla la fracción generatriz de 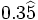 (Método corto)
(Método corto)
Halla la fracción generatriz de 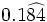 (Método corto)
(Método corto)
Halla la fracción generatriz de 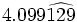 (Método corto)
(Método corto)
Halla la fracción generatriz por el método corto de:
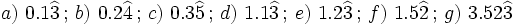
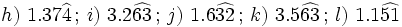
Actividad en la que debes pasar de decimal periódico mixto a fracción.
Ejercicios de autoevaluación sobre fracciones generatrices.
Ejemplos: Paso de decimal a fracción
Expresa en forma de fracción los números decimales:
- a)
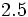
- b)
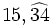
- c)
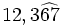
a) 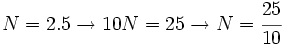
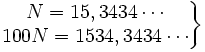 Restando:
Restando: 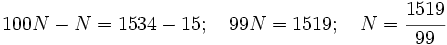 c)
c)  Restando:
Restando: 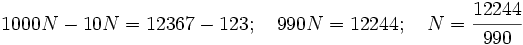
|
Calculadora: Fracciones. Paso a decimal y viceversa |
Actividades
1) Aproxima al entero o decimal exacto más cercano:
a) 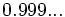 ; b)
; b) 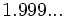 ; c)
; c) 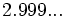 ; d)
; d) 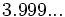 ; e)
; e) 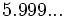 ; f)
; f) 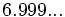 ; g)
; g) 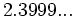 ;
;
h) 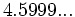 ; i)
; i) 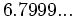 ; j)
; j) 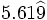 ; k)
; k) 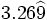 ; l)
; l) 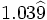
2) Halla las siguiente división: 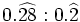 >.
>.
Halla:
- a)
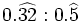
- b)
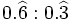
- c)
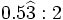
- d)

- e)

Obtención de fracciones generatrices planteando ecuaciones.
Obten la fracción generatriz de un número decimal:
Pulsa el botón "EJERCICIO" para generar una fracción. Debes averiguar de que tipo de expresión decimal se trata sin hacer la división. Luego halla su expresión decimal.
Lo haces en tu cuaderno, escribe la solución en la casilla "Expresión Decimal" y pulsa el botón "SOLUCIÓN" para ver si lo has hecho bien.
Números con infinitos decimales no periódicos
Los números decimales con infinitas cifras no periódicas no pueden ponerse en forma de fracción. Por tanto, no son racionales. Como por ejemplo:
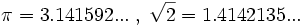
A estos números los llamaremos irracionales.
Ejercicios propuestos
|
Ejercicios propuestos: Paso de decimal a fracción |