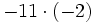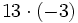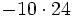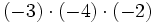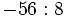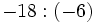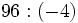Plantilla:Multiplicación y cociente de números enteros
De Wikipedia
| Revisión de 10:13 26 ago 2017 Coordinador (Discusión | contribuciones) (→Actividades y videotutoriales) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Propiedades de la división de números enteros) |
||
| Línea 3: | Línea 3: | ||
| {{p}} | {{p}} | ||
| ===Propiedades del producto de números enteros=== | ===Propiedades del producto de números enteros=== | ||
| - | {{Teorema_sin_demo|titulo=Propiedades de la multiplicación|enunciado= | + | {{Propiedades del producto de números enteros}} |
| - | *'''Operación interna''': El producto de dos números enteros es otro número entero: | + | |
| - | + | ||
| - | <center><math>a , \, b \in \mathbb{Z} \Rightarrow a \cdot b \in \mathbb{Z}</math> </center> | + | |
| - | + | ||
| - | *'''Propiedad conmutativa''': El producto no varía al cambiar el orden de los factores. | + | |
| - | {{p}} | + | |
| - | <center><math>a \cdot b = b \cdot a\,</math> </center>{{p}} | + | |
| - | *'''Propiedad asociativa''': El resultado de una multiplicación es independiente de la forma en que se agrupen los factores. | + | |
| - | {{p}} | + | |
| - | <center><math>(a + b ) + c = a + ( b + c )\,</math></center> | + | |
| - | *'''Propiedad distributiva''': El producto de un número por una suma (o resta) es igual a la suma (o resta) de los productos del número por cada sumando.{{p}} | + | |
| - | <center><math>a \cdot (b + c ) = a \cdot b + a \cdot c \qquad a \cdot (b - c ) = a \cdot b - a \cdot c</math> </center> | + | |
| - | {{p}} | + | |
| - | *'''Elemento neutro''': El elemento neutro para la multiplicación es el 1.{{p}} | + | |
| - | <center><math>1 \cdot a = a \,</math></center> | + | |
| - | + | ||
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | + | |
| - | + | ||
| - | '''Conmutativa:''' | + | |
| - | {{p}} | + | |
| - | <center><math>-8 \cdot 6 = 6 \cdot (-8)\,</math></center> | + | |
| - | {{p}} | + | |
| - | <center><math>-48 = -48\,</math></center> | + | |
| - | {{p}} | + | |
| - | '''Asociativa:''' | + | |
| - | {{p}} | + | |
| - | <center><math>( -3 \cdot 2 ) \cdot 6 = -3 \cdot ( 2 \cdot 6 )\,</math></center> | + | |
| - | {{p}} | + | |
| - | <center><math>-6 \cdot 6 = -3 \cdot 12\,</math></center> | + | |
| - | {{p}} | + | |
| - | <center><math>-36 = -36\,</math></center> | + | |
| - | {{p}} | + | |
| - | '''Distributiva:''' | + | |
| - | {{p}} | + | |
| - | <center><math> (-3) \cdot (2 + 6) = (-3) \cdot 2 + (-3) \cdot 6 \,</math></center> | + | |
| - | {{p}} | + | |
| - | <center><math>(-3) \cdot 8 = -6 - 18 \,</math></center> | + | |
| - | {{p}} | + | |
| - | <center><math>-24 = -24\,</math></center> | + | |
| - | {{p}} | + | |
| - | '''Elemento neutro:''' | + | |
| - | {{p}} | + | |
| - | <center><math> -3 \cdot 1 = -3\,</math></center> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| ==División o cociente de números enteros== | ==División o cociente de números enteros== | ||
| {{División o cociente de números enteros}} | {{División o cociente de números enteros}} | ||
| + | {{p}} | ||
| + | {{Actividades división enteros}} | ||
| {{p}} | {{p}} | ||
| ===Propiedades de la división de números enteros=== | ===Propiedades de la división de números enteros=== | ||
| - | {{Teorema_sin_demo||titulo=Propiedades de la división de números enteros|enunciado= | + | {{Propiedades de la división de números enteros}} |
| - | *La división de de números enteros no siempre es un número entero. | + | |
| - | *La división de números enteros no tiene las mismas propiedades que producto. No tiene la propiedad conmutativa, ni la asociativa, ni la distributiva. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{AI_cidead | + | |
| - | |titulo1=División de números enteros | + | |
| - | |descripcion=#Actividad para aprender a dividir números enteros. | + | |
| - | #Actividad para practicar la división de números enteros. | + | |
| - | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena3/1quincena3_contenidos_3b.htm | + | |
| - | }} | + | |
| - | {{AI_vitutor | + | |
| - | |titulo1=Autoevaluación: ''División de números enteros'' | + | |
| - | |descripcion=Ejercicios de autoevaluación sobre divisiónes de números enteros. | + | |
| - | |url1=http://www.vitutor.com/di/e/a_6e.html | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
Revisión actual
Tabla de contenidos |
Multiplicación o producto de números enteros
Regla de los signos para el producto
- Si dos números enteros tienen el mismo signo su producto es un entero positivo.
- Si dos números enteros tienen distinto signo, el producto es un entero negativo.
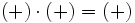 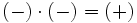 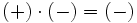 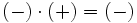 |
- Los paréntesis aparecen para separar los símbolos · y : de los símbolos + y -.
- Si el primer número es negativo no hace falta poner paréntesis.
- Cuando el signo (positivo) del segundo número no aparece escrito los paréntesis no son necesarios.
- a)
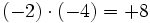
- b)
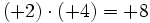
- c)

- d)
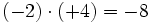
Aunque las expresiones anteriores son correctas, si nos atenemos a las reglas anteriores, los ejemplos b), c) y d) se podrían haber escrito de la siguiente manera más simple:
- b)
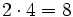
- c)
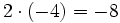
- d)
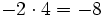
Producto de números enteros. Regla de los signos. Ejemplos
Producto de números enteros.
Aprende a usar la regla de los signos para multiplicar números enteros.
When number systems were expanded to include negative numbers, rules had to be formulated so that multiplication would be consistent regardless of the sign of the operands.
(Disponibles los subtítulos en inglés)
Opera:
- Actividad en la que se plantean problemas para aprender a multiplicar números enteros.
- Actividad para practicar la multiplicación de números enteros.
Practica el producto de números enteros
En esta escena podrás practicar la multiplicación de números enteros.
Si tienes problemas con la actividad a la hora de escribir las soluciones en los recuadros, haz lo siguiente:
- Haz click con el ratón en el cuadro donde va la repuesta.
- Pulsa "Enter".
- Te aparecerá el cursor y ya podrás escribir la solución.
Ejercicios de autoevaluación sobre multiplicaciones de números enteros.
Propiedades del producto de números enteros
Propiedades de la multiplicación
- Operación interna: El producto de dos números enteros es otro número entero:
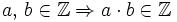
- Propiedad conmutativa: El producto no varía al cambiar el orden de los factores.
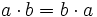
- Propiedad asociativa: El resultado de una multiplicación es independiente de la forma en que se agrupen los factores.
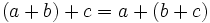
- Propiedad distributiva: El producto de un número por una suma (o resta) es igual a la suma (o resta) de los productos del número por cada sumando.

- Elemento neutro: El elemento neutro para la multiplicación es el 1.
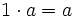
Gracias a la propiedad distributiva, tenemos dos opciones a la hora de enfrentarnos a unos paréntesis:
- Podemos realizar primero las operaciones que aparezcan dentro de los paréntesis.
- Podemos aplicar la propiedad distributiva y eliminar los paréntesis sin completar las operaciones que aparezcan dentro de ellos.
Esta propiedad es clave para realizar operaciones combinadas que veremos proximamente.
La propiedad distributiva tiene una especie de propiedad "recíproca" que llamaremos sacar factor comun. En realidad es la misma propiedad, pero usada "al revés". La idea es buscar un divisor común a todos los sumandos que tengamos y "sacarlo" fuera del paréntesis en el que meteremos al resultado de dividir a cada uno de los sumandos por ese factor.
- a) En este primer ejemplo sacaremos 3 como factor común:
- b) En este otro sacaremos 5 como factor común:
Sacar factor común no nos será especialmente útil en este tema, sin embargo, si será de gran utilidad, más adelante, cuando trabajemos con expresiones algebraicas.
- Propiedades del producto de números enteros. Ejemplos.
- Ejercicios:
1) Calcula:
- a)
![[(-4) \cdot (-2)] \cdot 6\;](/wikipedia/images/math/4/4/a/44a47677fd91afc7f8ed6c96632ec942.png)
- b)
![(-4) \cdot [(-2)] \cdot 6]\;](/wikipedia/images/math/b/1/9/b1976f580931741859d782c6d3346a15.png)
- c)
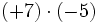
- d)
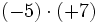
1) Calcula:
- a)
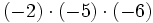
- b)
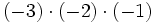
- c)
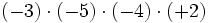
- d)
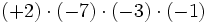
2) Calcula:
- a)
![[(-7) + (-3)] \cdot (+2)\;](/wikipedia/images/math/3/4/5/345ca286da82e44f4d7417853d6141b5.png)
- b)
![[(+4) - (+5)] \cdot (-3)\;](/wikipedia/images/math/6/d/6/6d6c19c9fa1c521567b33701a91f3a7c.png)
- c)
![(-5) \cdot [(+9) - (-5)]\;](/wikipedia/images/math/c/3/e/c3edcc45ed3f7456bfa1673b3a0d4f8a.png)
- d)
![(+2) \cdot [(+5) + (-2)]\;](/wikipedia/images/math/2/8/5/2856468702b11cb88edb046851bd6089.png)
3) Saca factor común:
- a)
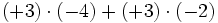
- b)
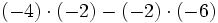
- c)
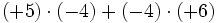
- d)
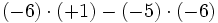
4) Sabiendo que a=-2, b=-3 y c=-1, calcula:
- a)
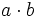
- b)

- c)
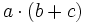
- d)
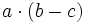
5) Completa la tabla (Ejercicios con operaciones y valor absoluto de números enteros)
6) Saca factor común descomponiendo previamente en producto de factores:
- a)
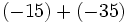
- b)
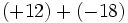
- c)
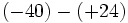
- d)
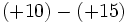
Ejercicios de autoevaluación sobre la propiedad distributiva del producto de enteros.
Ejercicios de autoevaluación sobre sacar factor común.
División o cociente de números enteros
Regla de los signos para el cociente
Con la división , al igual que con la multiplicación, se aplica la misma regla de los signos:
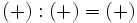 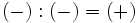 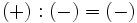 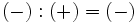 |
División o cociente de números enteros. Ejemplos.
División o cociente de números enteros. Ejemplos.
Cociente de números enteros.
- Actividad para aprender a dividir números enteros.
- Actividad para practicar la división de números enteros.
Practica el cociente de números enteros.
Ejercicios de autoevaluación sobre divisiónes de números enteros.
Propiedades de la división de números enteros
Propiedades de la división de números enteros
- La división de de números enteros no siempre es un número entero.
- La división de números enteros no tiene las mismas propiedades que producto. No tiene la propiedad conmutativa, ni la asociativa, ni la distributiva.
Al no tener la división de números enteros la propiedad asociativa, si aparecen varias divisiones consecutivas, sin paréntesis, tienen que hacerse de izquierda a derecha.
Fíjate en las siguientes operaciones:
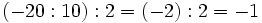
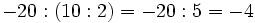
Por tanto, la división no es asociativa, así que si nos encontramos una cuenta como la de este ejemplo, pero sin paréntesis, tendremos que hacer las divisiones de izquierda a derecha, sin alterar el orden.
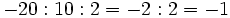
Ejercicios de autoevaluación sobre las propiedades del producto y cociente de números enteros.
Actividades y videotutoriales
Multiplicación y división de enteros. Regla de los signos.
Tutorial en el que se explica a través de varios ejemplos la multiplicación y división de números enteros, desde el caso en el que sólo intervienen dos números hasta cuando intervienen más.
- 00:00 a 06:38: Multiplicación y División simple de número enteros. (00:38 : Regla de los Signos.)
- 06:38 a 07:33: Ejercicios de Multiplicación y División simple.
- 07:33 a 12:30: Multiplicación y División compuesta de números enteros.
- 12:30 a 17:34: Ejercicios de Multiplicación y División compuesta.
Calcula:
Ejercicios sencillos de multiplicación y división de enteros.
Multiplicación y división:
Multiplicación y división de números enteros.
Introduce el resultado y cuando termines pulsa el botón "Corregir" de la parte inferior de la escena. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Ejercicios de autoevaluación sobre producto y cociente de números enteros.
En esta escena podrás practicar la multiplicación y división de números enteros.
Ejercicios de autoevaluación sobre multiplicaciones y divisiones de números enteros.
Ejercicios de autoevaluación sobre las propiedades del producto y del cociente de números enteros.
Suma, resta, multiplicación y división:
En esta escena podrás practicar la suma, resta, multiplicación y división de números enteros.
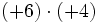
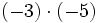
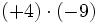
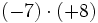
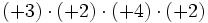
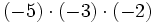
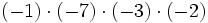
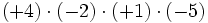
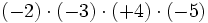
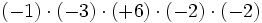
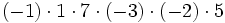
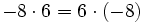
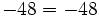
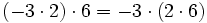
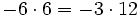
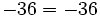
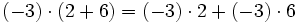
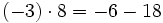
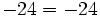
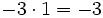
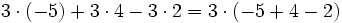
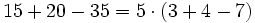
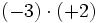
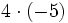
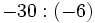
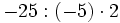
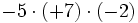
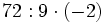
![-42 : [(-6) \cdot (-7)]\;](/wikipedia/images/math/9/7/b/97bf06a97f3e09f1e0dd13d3c5886e5a.png)
![[(+9) \cdot (-4)] : [-3 \cdot (+2)]\;](/wikipedia/images/math/0/8/5/0855f0174d3388d983075ce2f5995c46.png)