Números reales
De Wikipedia
| Revisión de 19:31 23 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:35 23 nov 2017 Coordinador (Discusión | contribuciones) (→Números reales) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Números reales== | ==Números reales== | ||
| - | {{Caja_Amarilla|texto=Los números [[Números racionales|racionales]] y los [[Números irracionales|irracionales]] forman el conjunto de los '''números reales''' y se designa con la letra <math>\mathbb{R}</math>}} | + | {{Def numeros reales}} |
| + | {{p}} | ||
| + | {{Videos y actividades: números reales}} | ||
| {{p}} | {{p}} | ||
Revisión de 19:35 23 nov 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Números reales
El conjunto de los números reales es el formado por la unión de los números racionales y de los números irracionales y se designa por 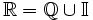 En el siguiente esquema puedes ver todos los conjuntos númericos con los que hemos trabajado hasta ahora: 
| 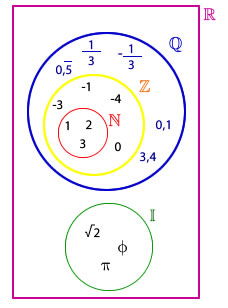 El conjunto de los números realesde portaleduativo.net |
Números naturales, enteros, racionales, irracionales y reales. Ejemplos.
Todo lo que necesitas saber sobre los distintos tipos de números reales (naturales, enteros, racionales e irraciones). Tutorial que explica de forma matemática y no tan matemática los conjuntos numéricos y como han ido surgiendo en demanda a las necesidades a la hora de poder resolver problemas aritméticos.
Introducción a números racionales e irracionales.
Clasifica en racionales e irracionales los siguientes números:
Clasificación de números reales.
Escena en la que se resume los distintos tipos de conjuntos nunéricos vistos hasta ahora.
Clasifica los siguientes números en racionales e irracionales.
Indica a que conjuntos de números pertenece un número dado.
Pulsa el botón "Ejercicio" para generar un ejercicio. Te dan un número y debes decir todos los conjuntos a los que pertenece. Luego pulsa el botón "Solución" para ver si lo has hecho bien.
Copia los ejercicios que hagas en tu cuaderno.
Ejercicios de autoevaluación sobre números reales.
Representación de los números reales
Cuando en una recta se representan los números racionales e irracionales se obtiene la recta real. Cualquier punto de la recta real representa un número real. .
|
Actividad Interactiva: Representación de los números reales
Actividad 1. Representación gráfica de los números reales en la recta real.
Actividad: Mueve el punto rojo y observa que todo punto de la recta representa un número real. Utiliza el zoom para ampliar la vista, si lo deseas. Luego introduce distintos número y observa su representación en la recta real:
|
Orden en el conjunto de los reales
Dados dos números reales  y
y  , se dice que
, se dice que  es menor que
es menor que  ,
, 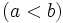 si
si  está más a la derecha que
está más a la derecha que  en la recta real. O dicho de otra forma, si
en la recta real. O dicho de otra forma, si 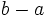 es positivo
es positivo 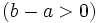
|
Actividad Interactiva: Orden en el conjunto de los reales
Actividad 1. Comparando dos números reales por su ubicación en la recta real.
Actividad: Pulsa "inicio" para ver ejemplos. Fíjate que el punto rojo representa un número más pequeño que el punto azul. Mueve el punto rojo. Si los números se salen de pantalla, utiliza el zoom. |
Ejercicios
|
Actividad Interactiva: Conjuntos numéricos
Actividad 1. Indica a que conjuntos de números pertenece un número dado.
Actividad: Pulsa el botón "Ejercicio" para generar un ejercicio. Te dan un número y debes decir todos los conjuntos a los que pertenece. Luego pulsa el botón "Solución" para ver si lo has hecho bien. Copia los ejercicios que hagas en tu cuaderno. |
 .
.
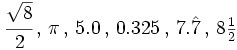
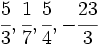 (teclea a/b para introducir la fracción
(teclea a/b para introducir la fracción  )
)

