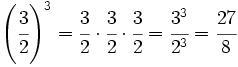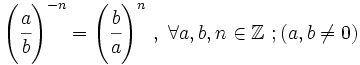Potencias de fracciones (2º ESO)
De Wikipedia
| Revisión de 17:32 1 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) |
||
| Línea 9: | Línea 9: | ||
| (Pág. 78) | (Pág. 78) | ||
| {{p}} | {{p}} | ||
| + | ==Potencia de una fracción== | ||
| + | {{Def: potencia fracción}} | ||
| + | {{p}} | ||
| + | {{AI_melide | ||
| + | |titulo1=Actividad | ||
| + | |descripcion=Potencias y raíces de fracciones. | ||
| + | ---- | ||
| + | '''Nota:''' Esta actividad también incluye raíces de fracciones. En el siguiente enlace puedes ver acerca de ellas. | ||
| + | |||
| + | [http://maralboran.org/web_ma/Melide/Operaciones_con_fracciones/Potenciasyraicesfracciones.html Potencias y raíces de fracciones] | ||
| + | |url1=http://maralboran.org/web_ma/Melide/Operaciones_con_fracciones/Ejercicios_3.html | ||
| + | }} | ||
| + | |||
| ==Potencias de exponente negativo== | ==Potencias de exponente negativo== | ||
| {{Def potencia exponente entero}} | {{Def potencia exponente entero}} | ||
| Línea 14: | Línea 27: | ||
| {{AI potencias exponente entero}} | {{AI potencias exponente entero}} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Propiedades de las potencias de números racionales== | ==Propiedades de las potencias de números racionales== | ||
| - | Las potencias con números racionales cumplen las mismas propiedades que con números enteros. | + | {{Propiedades de las potencias de números racionales}} |
| - | + | ||
| - | Ver: [[Potencias y raíces de números enteros (2º ESO)#Propiedades de las potencias de enteros|'''Propiedades de las potencias de números enteros''']] | + | |
| - | {{p}} | + | |
| - | {{propiedades potencias naturales}} | + | |
| - | {{p}} | + | |
| - | {{Videos ejemplos propiedades potencias fracciones}} | + | |
| - | {{p}} | + | |
| - | {{Ejemplo|titulo=Ejemplos: ''Potencias de fracciones''|enunciado=Calcula simplificando previamente: | + | |
| - | + | ||
| - | a) <math>\left( \cfrac{7}{6}\right)^4 \cdot \left( \cfrac{3}{7}\right)^4</math>{{b4}}{{b4}}b) <math>\left( \cfrac{3}{10}\right)^3 : \left( \cfrac{6}{5}\right)^3</math>{{b4}}{{b4}}c) <math>\left( \cfrac{3}{4}\right)^2 \cdot \left( \cfrac{3}{4}\right)^3</math>{{b4}}{{b4}} | + | |
| - | + | ||
| - | d) <math>\left( \cfrac{3}{4}\right)^4 : \left( \cfrac{3}{4}\right)^2</math>{{b4}}{{b4}}e) <math>\left(\left( \cfrac{1}{2}\right)^2 \right)^2</math>{{b4}}{{b4}}f) <math>\left( \cfrac{3}{5}\right)^0</math> | + | |
| - | |sol= | + | |
| - | a)<math>\left( \cfrac{7}{6}\right)^4 \cdot \left( \cfrac{3}{7}\right)^4=\left( \cfrac{3}{7} \cdot \cfrac{7}{6} \right)^4 = \left( \cfrac{3 \cdot \not{7}}{\not{7} \cdot 6} \right)^4 = \left( \cfrac{3}{6} \right)^4= \left( \cfrac{1}{2} \right)^4=\cfrac{1^4}{2^4}=\cfrac{1}{16}</math> | + | |
| - | ---- | + | |
| - | b)<math>\left( \cfrac{3}{10}\right)^3 : \left( \cfrac{6}{5}\right)^3=\left( \cfrac{3}{10} : \cfrac{6}{5}\right)^3=\left(\cfrac{3 \cdot 5}{10 \cdot 6}\right)^3=\left(\cfrac{3 \cdot 5}{5 \cdot 2 \cdot 3 \cdot 2}\right)^3=\left(\cfrac{\not{3} \cdot \not{5}}{\not{5} \cdot 2 \cdot \not{3} \cdot 2}\right)^3=\left(\cfrac{1}{4}\right)^3=\cfrac{1^3}{4^3}=\cfrac{1}{64}</math> | + | |
| - | ---- | + | |
| - | c)<math>\left( \cfrac{3}{4}\right)^2 \cdot \left( \cfrac{3}{4}\right)^3=\left( \cfrac{3}{4}\right)^{2+3}=\left( \cfrac{3}{4}\right)^5=\cfrac{3^5}{4^5}=\cfrac{243}{1024}</math> | + | |
| - | ---- | + | |
| - | d)<math>\left( \cfrac{3}{4}\right)^4 : \left( \cfrac{3}{4}\right)^2=\left( \cfrac{3}{4}\right)^{3-2}=\left( \cfrac{3}{4}\right)^1=\cfrac{3}{4}</math> | + | |
| - | ---- | + | |
| - | e) <math>\left(\left( \cfrac{1}{2}\right)^2 \right)^2=\left( \cfrac{1}{2}\right)^{2 \cdot 2}=\left( \cfrac{1}{2}\right)^4=\cfrac{1^4}{2^4}=\cfrac{1}{16}</math> | + | |
| - | ---- | + | |
| - | f) <math>\left( \cfrac{3}{5}\right)^0=1</math> | + | |
| - | }} | + | |
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
| Línea 48: | Línea 37: | ||
| (Pág. 80) | (Pág. 80) | ||
| - | [[Imagen:red_star.png|12px]] 1; 2a,c,d,e; 3a,d,f; 4a,d,f; 5a,c,e; 6a,c,e; 7a,c,e; 8a,d; 9a,d; 11a,c,e; 12; 13; 14 | + | [[Imagen:red_star.png|12px]] 1; 2a,c,d,e; 3a,d,f; 4a,d,f; 5a,c,e; 6a,c,e; 7a,c,e; 8a,d; 9a,d; 10a,d; 11a,c,e; 12; 13; 14 |
| - | [[Imagen:yellow_star.png|12px]] 2b,f; 3b,c,e; 4b,c,e; 5b,d,f; 6b,d,f; 7b,d,f; 8b,c; 9c,e; 11b,d,f; | + | [[Imagen:yellow_star.png|12px]] 2b,f; 3b,c,e; 4b,c,e; 5b,d,f; 6b,d,f; 7b,d,f; 8b,c; 9c,e; 10b,c; 11b,d,f; |
| |sol= | |sol= | ||
| }} | }} | ||
| - | ==Potencias de base 10== | + | |
| - | ===Expresión abreviada de números grandes=== | + | |
| - | {{Expresión abreviada de números grandes}} | + | |
| - | {{p}} | + | |
| - | ===Descomposición polinómica de un número=== | + | |
| - | {{Descomposición polinómica de un número}} | + | |
| - | {{p}} | + | |
| - | ===Notación científica=== | + | |
| [[Categoría: Ejercicios de Matemáticas|Números]] | [[Categoría: Ejercicios de Matemáticas|Números]] | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 78)
Potencia de una fracción
Procedimiento: Potencia de una fracción
Para elevar una fracción a una potencia se eleva el numerador y el denominador a dicha potencia.
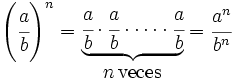
Potencias y raíces de fracciones.
Nota: Esta actividad también incluye raíces de fracciones. En el siguiente enlace puedes ver acerca de ellas.
Potencias y raíces de fracciones
Potencias de exponente negativo
Se define la potencia de exponente negativo como:

Como consecuencia:
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos.
 . Ejemplos.
. Ejemplos.
Exponentes negativos. Ejemplos.
Razonando sobre el por qué de la definición de los exponentes negativos.
Simplifica:
- a)
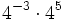
- b)
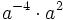
- c)
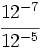
- d)
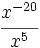
Simplifica:
- a)
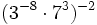
- b)
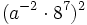
- c)
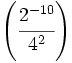
Halla el valor de:
11) 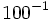 ; 12)
; 12) 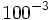 ; 13)
; 13) 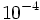 ; 14)
; 14) 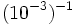
15) 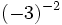 ; 16)
; 16) 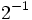 ; 17)
; 17) 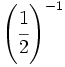 ; 18)
; 18) 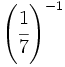 ; 19)
; 19) 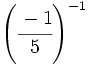
Potencias de exponente negativo.
Actividades sobre potencias de exponente negativo.
Calcula las siguientes potencias y comprueba los resultados en la escena siguiente:
a) 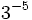 b)
b) 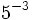 c)
c) 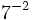 d)
d) 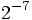
Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba.
Potencias de exponente negativo.
Multiplica y divide potencias (exponentes enteros).
Potencias de productos y cocientes (exponentes enteros)
Potencias de exponentes enteros.
Pulsa el botón "EJERCICIO" y lee atentamente el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien.
Ejercicios de autoevaluación sobre potencias de exponente negativo.
Propiedades de las potencias de números racionales
Las potencias con números racionales cumplen las mismas propiedades que con números enteros.
Ver: Propiedades de las potencias de números enteros
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
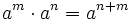
- 2. Cociente de potencias de la misma base:
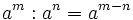
- 3. Potencia de un producto:
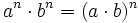
- 4. Potencia de un cociente:
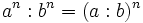
- 5. Potencia de otra potencia:
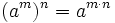
Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa.
Simplifica:
- a)
![\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3](/wikipedia/images/math/f/e/c/fec21991837955f9b9d945d4600cba18.png)
- b)
![\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2}](/wikipedia/images/math/e/5/1/e5178ed20376c4ef7f07ca88d5d43975.png)
Simplifica 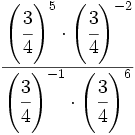
Simplifica: ![\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2](/wikipedia/images/math/6/9/1/6911b07dbbc54e802f87f7498ab77b09.png)
Ejemplos: Potencias de fracciones
Calcula simplificando previamente:
a) 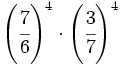 b)
b) 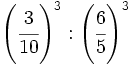 c)
c) 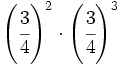
d) 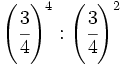 e)
e) 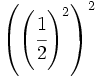 f)
f) 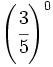
a)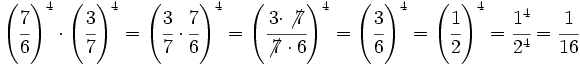
b)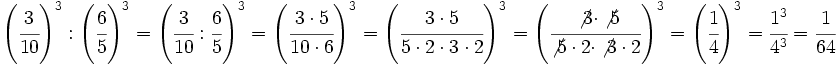
c)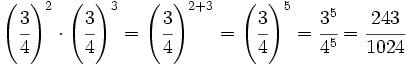
d)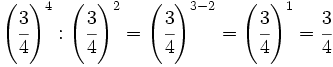
e) 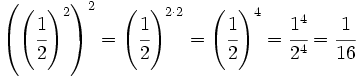
f)
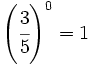
Ejercicios de autoevaluación sobre potencias de fracciones.
Ejercicios de autoevaluación sobre potencias de exponente negativo.
Ejercicios de autoevaluación sobre potencias de números racionales.
Ejercicios propuestos
|
Ejercicios propuestos: Potencias de fracciones |