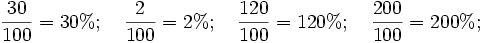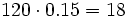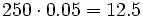Porcentajes
De Wikipedia
| Revisión de 13:09 13 sep 2016 Coordinador (Discusión | contribuciones) (→Obtención del porcentaje correspondiente a una proporción) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Menú Matemáticas 3ESO | + | {{Menú Matemáticas Contenidos Generales |
| |ir= | |ir= | ||
| |ampliar= | |ampliar= | ||
| - | |repasar=[[Proporcionalidad y porcentajes(1º ESO)|Proporcionalidad]] | + | |repasar= |
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| Línea 12: | Línea 12: | ||
| Podemos representar gráficamente estos porcentajes igual que se hace con las fracciones. | Podemos representar gráficamente estos porcentajes igual que se hace con las fracciones. | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas: ''Representación de porcentajes'' | + | {{representacion porcentajes}} |
| - | |cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1.''' En la siguiente escena se pueden representar porcentajes. | + | |
| - | |actividad= | + | |
| - | Cambia el valor del porcentaje mediante las flechitas o introduciendo el número y pulsando "Intro".{{p}} | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/wiki3eso/numeros/porcentajes/repres_porcentaje.html | + | |
| - | width=100% | + | |
| - | height=400 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/wiki3eso/numeros/porcentajes/repres_porcentaje.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| ==Cálculo de un tanto por ciento de una cantidad== | ==Cálculo de un tanto por ciento de una cantidad== | ||
| - | {{Caja_Amarilla|texto=Para calcular el tanto por ciento de una cantidad, se expresa el tanto por ciento en forma decimal (dividiéndolo por 100) y se multiplica por la cantidad.{{p}} | + | {{calculo del porcentaje}} |
| - | <center><math>El \ n% \ de \ C = \cfrac{n}{100} \cdot C</math></center> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Cálculo de un porcentaje'' | + | ===Elementos que intervienen en el cálculo de porcentajes=== |
| - | |enunciado= | + | {{Elementos que intervienen en el cálculo de porcentajes}} |
| - | Calcula el 16% de 2000. | + | |
| - | |sol= | + | |
| - | '''Método 1: A partir de la definición de pordentaje:''' | + | |
| - | + | ||
| - | El 16% de 2000<math>= \frac{16}{100} \cdot 2000=0,16 \cdot 2000=320</math> | + | |
| - | + | ||
| - | '''Método 2: Mediante una regla de tres''' | + | |
| - | + | ||
| - | 100% ----> 2000 | + | |
| - | 16% ----> x | + | |
| - | + | ||
| - | Y despejando <math>x\;\!</math>: | + | |
| - | + | ||
| - | <center><math>x=\frac{16 \cdot 2000}{100}= 320</math></center> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas: ''Cálculo de porcentajes'' | + | ===Cálculo de la cantidad total a partir del porcentaje=== |
| - | |cuerpo= | + | {{porcentaje inverso}} |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1.''' Calcula los siguientes porcentajes en tu cuaderno y luego comprueba los resultados en la escena. | + | |
| - | :a) 10% de 43; b) 60% de 200; c) 50% de 40; d) 5% de 1000; e) 25% de 400. | + | |
| - | {{p}} | + | |
| - | |actividad= | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/wiki3eso/numeros/porcentajes/calculo_porcentaje.html | + | |
| - | width=100% | + | |
| - | height=200 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/wiki3eso/numeros/porcentajes/calculo_porcentaje.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 2.''' Calcula mentalmente. | + | |
| - | |actividad= | + | |
| - | ¿Qué resultado es el correcto? Pincha con el ratón el punto rojo y llévalo a la caja del número que te parezca correcto. Para hacer otro ejercicio pulsa el botón inicio | + | |
| - | {{p}} | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/wiki3eso/numeros/porcentajes/calculo_porcentaje2.html | + | |
| - | width=100% | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/wiki3eso/numeros/porcentajes/calculo_porcentaje2.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Ejemplo|titulo=Ejemplo: ''Cálculo de la cantidad total a partir del porcentaje'' | + | |
| - | |enunciado= | + | |
| - | Si en una clase hay 5 alumnos rubios, y representan el 20% de la clase, ¿cuántos alumnos hay en total? | + | |
| - | |sol= | + | |
| - | '''Método 1: A partir de la definición de pordentaje:''' | + | |
| - | + | ||
| - | Si llamamos <math>C\;\!</math> al total de alumnos de la clase: | + | |
| - | + | ||
| - | <center><math>5=\frac{20}{100} \cdot C </math></center> | + | |
| - | + | ||
| - | Y despejando <math>C\;\!</math>: | + | |
| - | + | ||
| - | <center><math>C=\frac{5 \cdot 100}{20}= 25 \ alumnos</math></center> | + | |
| - | + | ||
| - | '''Método 2: Mediante una regla de tres''' | + | |
| - | + | ||
| - | 20% ----> 5 alumnos | + | |
| - | 100% ----> x alumnos | + | |
| - | + | ||
| - | Y despejando <math>x\;\!</math>: | + | |
| - | + | ||
| - | <center><math>x=\frac{5 \cdot 100}{20}= 25 \ alumnos</math></center> | + | |
| - | + | ||
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | ==Obtención del porcentaje correspondiente a una proporción== | + | ===Cálculo del porcentaje conocida una parte y el total=== |
| {{Porcentaje de proporcion}} | {{Porcentaje de proporcion}} | ||
| {{p}} | {{p}} | ||
| ==Aumentos y disminuciones porcentuales== | ==Aumentos y disminuciones porcentuales== | ||
| - | {{Caja_Amarilla|texto= | + | {{Aumentos y disminuciones porcentuales}} |
| - | *Un '''aumento porcentual''' es añadir un porcentaje a una cierta cantidad y una '''disminución porcentual''' es quitar un porcentaje a una cierta cantidad. | + | |
| - | <br> | + | |
| - | *El número por el que hay que multiplicar la cantidad inicial para obtener la cantidad final se llama '''índice de variación'''. | + | |
| - | {{p}} | + | |
| - | {{Caja|contenido= | + | |
| - | <center> <math>Cantidad \ Final = Cantidad \ Inicial \cdot \acute{I}ndice \ de \ Variaci \acute{o} n</math> </CENTER> | + | |
| - | }} | + | |
| - | <br> | + | |
| - | *En '''aumentos porcentuales''' del n%, el índice de variación es 1 más el aumento porcentual expresado en forma decimal. | + | |
| - | {{p}} | + | |
| - | {{Caja|contenido= | + | |
| - | <center> <math>Cantidad \ Final = Cantidad \ Inicial \cdot \left(1+\cfrac{n}{100} \right)</math> </CENTER> | + | |
| - | }} | + | |
| - | <br> | + | |
| - | *En una '''disminución porcentual''' del n%, el índice de variación es 1 menos la disminución porcentual puesta en forma decimal. | + | |
| - | {{p}} | + | |
| - | {{Caja|contenido= | + | |
| - | <center> <math>Cantidad \ Final = Cantidad \ Inicial \cdot \left(1-\cfrac{n}{100}\right)</math> </CENTER> | + | |
| - | }} | + | |
| - | + | ||
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Ejemplo|titulo=Ejemplo: ''Aumento y disminución porcentual'' | + | |
| - | |enunciado= | + | |
| - | :a) Un litro de leche de 0,95 € aumenta su precio en un 12% ¿Cuánto vale ahora? | + | |
| - | :b) Unas zapatillas de 120 € se rebajan un 15% ¿Cuál es el valor final? | + | |
| - | |sol= | + | |
| - | a) <math>0,95 \cdot (1+0,12)=0,95 \cdot 1,12=1,064\approx 1,06</math> € | + | |
| - | b) <math> 120 \cdot (1-0,15)=120 \cdot 0,85=102 </math> € | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{AI2|titulo=Actividades Interactivas: ''Aumentos y disminuciones porcentuales'' | + | |
| - | |cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1.''' Calcula los siguientes aumentos porcentuales en tu cuaderno y luego comprueba los resultados en la escena. | + | |
| - | + | ||
| - | a) En un instituto hay un 12% más de alumnas que de alumnos. ¿Cuántas alumnas hay sabiendo que hay 150 alumnos? | + | |
| - | + | ||
| - | b) El precio de una bicicleta que costaba 400 € el año pasado, ha subido un 20%.¿Cuál es el precio actual? | + | |
| - | + | ||
| - | c) Actualmente me dan 15 € mensuales de paga, pero he convencido a mis padres para que me suban el 15%. ¿Cuál será mi paga a partir de ahora? | + | |
| - | + | ||
| - | d) ¿Cuánto hay que pagar por un disco de 15 € si hay que sumarle el 16% de IVA? | + | |
| - | + | ||
| - | e) La factura de teléfono de este mes es de 45 € sin IVA. ¿Cuanto será al añadirle el 16% de IVA? | + | |
| - | + | ||
| - | f) ¿Cuánto nos costará dormir una noche en un hotel sabiendo que la habitación vale 70 € sin IVA y el IVA es del 7%? | + | |
| - | + | ||
| - | |actividad= | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/wiki3eso/numeros/porcentajes/Aumentos_porcentuales.htm | + | |
| - | width=100% | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/wiki3eso/numeros/porcentajes/Aumentos_porcentuales.htm '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 2.''' Calcula las siguientes disminuciones porcentuales en tu cuaderno y luego comprueba los resultados en la escena. | + | |
| - | + | ||
| - | a) Un ordenador cuesta este año 850 €. ¿Cuánto costará el año que viene sabiendo que perderá el 40% de su valor? | + | |
| - | + | ||
| - | b) Mis padres me han dado 40 € por mi cumpleaños. ¿Cuánto me quedará al final del día si me gasto el 80% de lo que me han dado? | + | |
| - | + | ||
| - | c) Un trabajador tiene un salario bruto de 980 € al mes, del que le descuentan un 12% en impuestos. ¿Qué salario neto percibe? | + | |
| - | + | ||
| - | d) En una tienda hacen una rebaja del 20% a todos los artículos. ¿Cuanto costará ahora una camisa que antes costaba 35 €? ¿Y un pantalón de 40 €? | + | |
| - | + | ||
| - | e) Tengo 52 € y me quiero comprar un MP3 que costaba antes de las rebajas 60 €. ¿Podré pagarlo si lo rebajan un 15%? | + | |
| - | + | ||
| - | f) Quiero comprarme unas zapatillas de deporte. En una tienda veo dos que me gustan; las primeras tienen un precio de 45 € y una rebaja del 30% y las segundas cuestan 35 € pero no tienen rebaja. ¿Cuáles salen más baratas? | + | |
| - | + | ||
| - | |actividad= | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/wiki3eso/numeros/porcentajes/disminuciones_porcentuales.htm | + | |
| - | width=100% | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/wiki3eso/numeros/porcentajes/disminuciones_porcentuales.htm '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| ==Calculo de la cantidad inicial conociendo la variación porcentual y la cantidad final== | ==Calculo de la cantidad inicial conociendo la variación porcentual y la cantidad final== | ||
| - | + | {{cantidad inicial sabiendo variacion porcentual}} | |
| - | {{Caja_Amarilla|texto= | + | |
| - | La cantidad inicial se calcula '''dividiendo''' la cantidad final por el índice de variación. | + | |
| - | {{Caja|contenido= | + | |
| - | <center><math>Cantidad \ Inicial = \cfrac{Cantidad \ Final}{\acute{I}ndice \ de \ Variaci \acute{o} n}</math></center> | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Ejemplo|titulo=Ejemplo: ''Cálculo de la cantidad inicial'' | + | |
| - | |enunciado= a) El precio de una moto es de 2800 €. ¿Cuál era el precio de fábrica antes de aplicarle el 16 % de aumento por el IVA?. | + | |
| - | + | ||
| - | b) En las rebajas has comprado unas zapatillas de 90 €, con un descuento del 28 %. ¿Cuánto valía antes de la rebaja? | + | |
| - | |sol=a) Por ser un aumento porcentual, el índice de variación es: 1 + 0,16 = 1,16. Por tanto, el precio inicial de la moto es | + | |
| - | <center><math> \frac{2800}{1,16}= 2413,79 </math>€</center> | + | |
| - | + | ||
| - | b) Por ser una disminución porcentual, el índice de variación es: 1 - 0,28 = 0,72. Por tanto, el precio inicial de la moto es | + | |
| - | <center><math> \frac{90}{0,72}= 125 </math>€</center> | + | |
| - | + | ||
| - | + | ||
| - | }} | + | |
| - | {{p}} | + | |
| ==Encadenamiento de variaciones porcentuales== | ==Encadenamiento de variaciones porcentuales== | ||
| - | {{Caja_Amarilla|texto= | + | {{Encadenamiento de variaciones porcentuales}} |
| - | Para encadenar aumentos y disminuciones porcentuales, se multiplican los índices de variación de los sucesivos pasos, siendo el producto el índice de variación del encadenamiento | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Ejemplo|titulo=Ejemplo: ''Encadenamiento porcentual'' | + | |
| - | |enunciado= El precio de un litro de gasoil era de 102 céntimos de € en el mes de Junio. Subió un 3% en el mes de Agosto y un 4% en el mes de Septiembre. | + | |
| - | :a) Calcula el precio final tras las dos subidas. | + | |
| - | :b) ¿Ha subido un 3+4=7%?. ¿Qué porcentaje a subido? | + | |
| - | |sol= | + | |
| - | a) El precio final es: <math>102 \cdot 1,03 \cdot 1,04= 109,2624</math> céntimos de € | + | |
| - | + | ||
| - | b) No, pués el índice de variación total es <math>1,03 \cdot 1,04 = 1,0712 \;\!</math>, es decir un aumento del <math>(1,0712-1) \cdot 100=7,12%</math>. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| {{ejercicio | {{ejercicio | ||
| Línea 258: | Línea 60: | ||
| }} | }} | ||
| }} | }} | ||
| + | |||
| + | ==Ejercicios y problemas== | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicios: ''Porcentajes'' | ||
| + | |duracion=16'03" | ||
| + | |sinopsis=Problemas con porcentajes. | ||
| + | |url1=https://www.youtube.com/watch?v=_LPPP8tK6eI&list=PL3KGq8pH1bFTEqvQj6O_p10Kc0oTP4nb2&index=39 | ||
| + | }} | ||
| + | {{Actividades: Porcentajes}} | ||
| [[Categoría: Matemáticas]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Números]] | ||
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | WIRIS Geogebra Calculadora |
Definición de porcentaje
- Un porcentaje es una razón entre un número n y 100 y representa las partes que tomamos de un total de 100.
- Se representa escribiendo el número seguido del símbolo %, esto es:
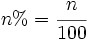 (se lee "
(se lee " por ciento")
por ciento")Representación de los porcentajes
Podemos representar gráficamente estos porcentajes igual que se hace con las fracciones.
Colorea el 20% de un cuadrado.
Colorea el 109% de un cuadrado.
Actividades para aprender y practicar con el significado de los porcentajes. Los porcentajes podemos verlos como fracción o como número decimal.
Actividades para aprender y practicar con el significado de los porcentajes. Los porcentajes podemos verlos como fracción o como número decimal.
Introducción a los porcentajes.
Porcentajes a partir de modelos de fracciones.
Relaciona fracciones, decimales y porcentajes.
Conversión entre porcentajes, fracciones y decimales
Hemos definido un porcentaje como una fracción y sabemos que una fracción se puede escribir como un número decimal. Por tanto, un porcentaje lo podemos expresar de tres formas equivalentes: como porcentaje, como fracción o como número decimal.
Convierte el decimal 0.601 a un porcentaje equivalente.
Convierte el decimal 1.501 a un porcentaje equivalente.
Convierte 59.2% en un decimal equivalente.
Convierte 113.9% en un decimal equivalente.
Convierte 18% en un decimal y en una fracción equivalente.
Conversión entre porcentajes, fracciones y decimales.
Repaso de conversión entre decimales y porcentajes.
Repaso de conversión entre porcentajes y fracciones.
Convertir decimales en porcentajes.
Convertir porcentajes en decimales.
Convertir porcentajes y fracciones.
Cálculo de un tanto por ciento de una cantidad
Cálculo del porcentaje
Para hallar el 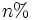 de una cantidad,
de una cantidad, 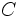 , podemos proceder de dos formas:
, podemos proceder de dos formas:
- Calculando la fracción de dicha cantidad:
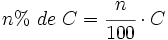
- Mediante una proporción (regla de tres directa):
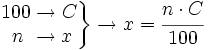
Ejemplo: Cálculo de porcentajes (2 métodos)
En un pueblo hay 2000 habitantes, de los cuales el 16% son niños. ¿Cuántos niños hay en el pueblo?
Método 1: A partir de la definición de porcentaje:
- El 16% de 2000
 niños
niños
Método 2: Mediante una regla de tres:
100% ----> 2000
16% ----> x
| 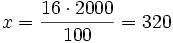 niños niños
|
Cálculo rápido de un porcentaje
Hemos visto que un porcentaje es equivalente a una razón de divisor 100, y dividir entre 100 es muy fácil (basta correr la coma decimal dos lugares a la izquierda). Así, si transformamos esa razón en un número decimal mentalmente, el cálculo del tanto por ciento se reduce a una simple multiplicación.
Cálculo rápido de un porcentaje
Calcular el n% de una cantidad equivale a multiplicar la cantidad por el número que resulta de dividir n entre 100.
Cálculo del procentaje de un número. Ejemplos.
Tutorial en el que se dan los conceptos matemáticos de proporción y porcentaje, viendo la información que aporta cada uno de ellos y cómo pasar de una forma a otra.
Definición de tanto por ciento. Ejemplos.
Definición de tanto por ciento. Ejemplos.
Definición de tanto por ciento. Ejemplos.
¿Cuál es el 12% de 75?
¿Cuál es el 30% de 6?
Gasté el 30% de mi dinero y regalé el 16% de lo que me quedó. Si al principio tenía 250€, ¿cuánto tengo ahora?
Problemas de cálculo del porcentajes por el método directo.
Calcula los siguientes porcentajes en tu cuaderno y luego comprueba los resultados en la escena.
- a) 10% de 43; b) 60% de 200; c) 50% de 40; d) 5% de 1000; e) 25% de 400.
Porcentajes sencillos
Hay algunos porcentajes que se pueden calcular fácilmente:
Procedimiento
- Calcular el 10% equivale a dividir por 10.
- Calcular el 20% equivale a dividir por 5.
- Calcular el 25% equivale a dividir por 4.
- Calcular el 50% equivale a dividir por 2.
Calcula mentalmente:
¿Qué resultado es el correcto? Pincha con el ratón el punto rojo y llévalo a la caja del número que te parezca correcto. Para hacer otro ejercicio pulsa el botón inicio
Elementos que intervienen en el cálculo de porcentajes
En cualquier situación con porcentajes están involucrados tres elementos: la cantidad total, la parte de esa cantidad y el propio tanto por ciento.
Estos tres elementos forman parte de una proporción con dos razones igualadas, una de las cuales siempre tiene el número 100 como denominador.
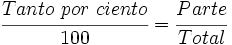
También podemos verlo como una regla de tres:
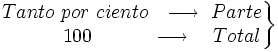
Cálculo de la cantidad total a partir del porcentaje
Ejemplo: Cálculo de la cantidad total a partir del porcentaje (porcentaje inverso)
Si en una clase hay 5 alumnos rubios, y representan el 20% de la clase, ¿cuántos alumnos hay en total?
Método 1: A partir de la definición de porcentaje:
Si llamamos 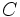 al total de alumnos de la clase:
al total de alumnos de la clase:
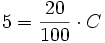
Y despejando 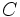 :
:
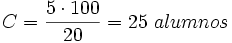
Método 2: Mediante una regla de tres
% alumnos
---- -------
Parte: 20 ----> 5
Total: 100 ----> x
Y despejando  :
:
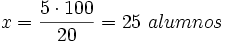
Cálculo del total conocida una parte y el porcentaje. Ejemplos.
Tutorial en el que se dan los conceptos matemáticos de porcentajes y se explica/justifica como calcular porcentajes de cantidades o bien la cantidad a la que se le aplicó una proporción.
¿De qué número es 300 el 40%?
¿De qué número es 150 el 25%?
¿De qué número es 78 es el 15%?
Hoy las guayabas estaban rebajadas un 30% en el mercado y por 6 unidades pagué $12.60. ¿Cuánto habría pagado por 2 guayabas si no hubiesen estado rebajadas?
Un zoológico tiene 15 pingüinos emperador que constituyen el 30% del total de pingüinos del zoológico. ¿Cuántos pingüinos hay en el zoológico?
Actividades en las que practicarás el cálculo del total conocida una parte y el porcentaje (porcentaje inverso), y de la parte conocido el total y el porcentaje (porcentaje directo).
Actividades de autoevaluación sobre cálculo de porcentajes inversos.
Cálculo del porcentaje conocida una parte y el total
Procentaje correspondiente a una proporción
Para hallar qué tanto por ciento representa una cantidad,  , repecto a un total,
, repecto a un total, 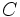 , se efectúa la siguiente operación:
, se efectúa la siguiente operación:
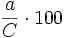
Ejemplo: Porcentaje correspondiente a una proporción
En un grupo del instituto, de 30 alumnos aprueban 21. ¿Qué porcentaje del total representan los aprobados?. ¿Y los suspensos?
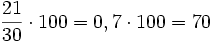
Por tanto el 70% aprueban y el 30% suspenden.
También podemos hacerlo mediante una regla de tres:
% alumnos
---- -------
Total: 100 ----> 30
Parte (aprobados): x ----> 21
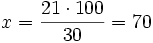
Cálculo del porcentaje conocida una parte y el total. Ejemplos.
¿Qué porcentaje es 425 de 500?
¿Qué porcentaje de 16 es 4?
¿Qué porcentaje es 100 de 80?
Un hotel tiene 300 habitaciones de las que 60 están vacías. ¿Cua´l es el porcentaje de ocupación?
En México 13 de cada 20 latas son recicladas. ¿Qué porcentaje de latas es reciclado?
Actividades en las que practicarás el cálculo del porcentaje conocida una parte y el total.
Actividades de autoevaluación sobre cálculo del porcentaje a partir de la parte y el total.
Aumentos y disminuciones porcentuales
- Un aumento porcentual es añadir un porcentaje a una cierta cantidad de partida.
- Una disminución porcentual es quitar un porcentaje a una cierta cantidad de partida.
- A la cantidad de partida la llamaremos cantidad inicial y al resultado cantidad final.
Proposición
En un aumento/disminución porcentual, se cumple:
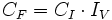
siendo 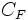 = Cantidad final,
= Cantidad final, 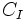 = Cantidad inicial e
= Cantidad inicial e 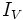 = Indice de variación.
= Indice de variación.
- En aumentos porcentuales del n%:
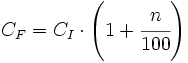
- En una disminuciones porcentuales del n%:
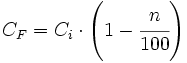
- En aumentos porcentuales del n%:
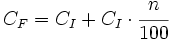
- Sacando factor común:
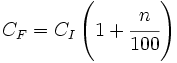
- En disminuciones porcentuales del n%:
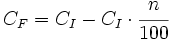
- Sacando factor común:
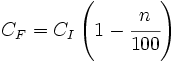
Los aumentos y disminuciones porcentuales también pueden efectuarse mediante reglas de tres directas, no obstante, el uso de índices de variación nos facilitará los cálculos cuando tengamos encadenamientos porcentuales.
Si quieres ver cómo se hace con reglas de tres puedes consultar el siguiente enlace:
Aumentos y disminuciones porcentuales usando reglas de tres
Ejemplo: Aumento y disminución porcentual
a) Un litro de leche de 0,95 € aumenta su precio en un 12% ¿Cuánto vale ahora?
b) Unas zapatillas de 120 € se rebajan un 15% ¿Cuál es el valor final?
a) 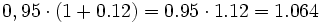 €
€
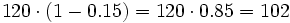 €
€Cálculo de aumentos y disminuciones porcentuales . Ejemplos.
Tutorial que explica los problemas de porcentajes y proporciones simples, es decir donde sólo interviene una variación, viendo distintos métodos para dar con la solución.
Cálculo de porcentajes y de incrementos y disminuciones porcentuales por el método directo. Ejemplos.
Problemas de cálculo de porcentajes y de incrementos y disminuciones porcentuales por el método directo.
Aumentos porcentuales:
Actividades en las que practicarás el cálculo de aumentos porcentuales.
Calcula los siguientes aumentos porcentuales en tu cuaderno y luego comprueba los resultados en la escena.
a) En un instituto hay un 12% más de alumnas que de alumnos. ¿Cuántas alumnas hay sabiendo que hay 150 alumnos?
b) El precio de una bicicleta que costaba 400 € el año pasado, ha subido un 20%.¿Cuál es el precio actual?
c) Actualmente me dan 15 € mensuales de paga, pero he convencido a mis padres para que me suban el 15%. ¿Cuál será mi paga a partir de ahora?
d) ¿Cuánto hay que pagar por un disco de 15 € si hay que sumarle el 16% de IVA?
e) La factura de teléfono de este mes es de 45 € sin IVA. ¿Cuánto será al añadirle el 16% de IVA?
f) ¿Cuánto nos costará dormir una noche en un hotel sabiendo que la habitación vale 70 € sin IVA y el IVA es del 7%?
Actividades en las que practicarás el cálculo de aumentos porcentuales.
Disminuciones porcentuales:
Actividades en las que practicarás el cálculo de disminuciones porcentuales.
Calcula las siguientes disminuciones porcentuales en tu cuaderno y luego comprueba los resultados en la escena.
a) Un ordenador cuesta este año 850 €. ¿Cuánto costará el año que viene sabiendo que perderá el 40% de su valor?
b) Mis padres me han dado 40 € por mi cumpleaños. ¿Cuánto me quedará al final del día si me gasto el 80% de lo que me han dado?
c) Un trabajador tiene un salario bruto de 980 € al mes, del que le descuentan un 12% en impuestos. ¿Qué salario neto percibe?
d) En una tienda hacen una rebaja del 20% a todos los artículos. ¿Cuanto costará ahora una camisa que antes costaba 35 €? ¿Y un pantalón de 40 €?
e) Tengo 52 € y me quiero comprar un MP3 que costaba antes de las rebajas 60 €. ¿Podré pagarlo si lo rebajan un 15%?
f) Quiero comprarme unas zapatillas de deporte. En una tienda veo dos que me gustan; las primeras tienen un precio de 45 € y una rebaja del 30% y las segundas cuestan 35 € pero no tienen rebaja. ¿Cuáles salen más baratas?
Actividades en las que practicarás el cálculo de disminuciones porcentuales.
Actividades en las que practicarás el cálculo de disminuciones porcentuales.
Aumentos y disminuciones porcentuales:
Actividades en las que practicarás el cálculo de aumentos y disminuciones porcentuales.
Si quieres puedes ver unos ejemplos antes de hacer la autoevaluación: [1]
Problemas de cálculo de aumentos y disminuciones porcentuales.
Calculo de la cantidad inicial conociendo la variación porcentual y la cantidad final
Proposición
La cantidad inicial se calcula dividiendo la cantidad final por el índice de variación:
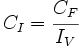
- Es inmediato, despejando
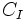 de la fórmula:
de la fórmula:
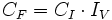
Ejemplo: Cálculo de la cantidad inicial
a) El precio de una moto es de 2800 €. ¿Cuál era el precio de fábrica antes de aplicarle el 16 % de aumento por el IVA?.
b) En las rebajas has comprado unas zapatillas de 90 €, con un descuento del 28 %. ¿Cuánto valía antes de la rebaja?
a) Por ser un aumento porcentual, el índice de variación es:
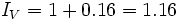
Por tanto, el precio inicial de la moto es
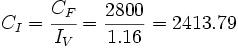 €
€b) Por ser una disminución porcentual, el índice de variación es:
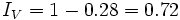
Por tanto, el precio inicial de la moto es
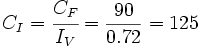 €
€Encadenamiento de variaciones porcentuales
Proposición
Para encadenar aumentos y disminuciones porcentuales, se multiplican los índices de variación de los sucesivos pasos, siendo el producto el índice de variación del encadenamiento.
Basta aplicar la fórmula
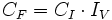
de forma reiterada, tomando como 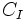 en cada paso, la
en cada paso, la 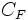 obtenida en el paso anterior.
obtenida en el paso anterior.
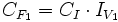
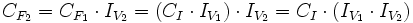

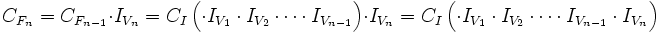
Ejemplo: Encadenamiento porcentual
El precio de un litro de gasoil era de 102 céntimos de € en el mes de Junio. Subió un 3% en el mes de Agosto y un 4% en el mes de Septiembre.
- a) Calcula el precio final tras las dos subidas.
- b) ¿Ha subido un 3+4=7%?. ¿Qué porcentaje ha subido?
a) El precio final es: 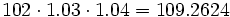 céntimos de €
céntimos de €
b) El índice de variación total es:
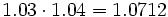
Al ser este índice de variación mayor que 1, corresponde a un aumento porcentual. Despejando n de la fórmula:
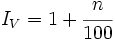
tenemos:
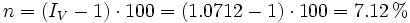
Problemas:
- Un depósito de agua tenía el lunes 4000 hl de agua. El martes, debido a las lluvias, aumentó su capacidad en un 20%, mientras que el miércoles perdió el 20% del agua que tenía el martes. ¿Qué cantidad de agua tiene actualmente?
- El domingo por la noche se dejó lleno un depósito. El lunes se vació el 40%, mientras que el martes se gastaron 3/4 de lo que quedaba. Si sobraron todavía 90 litros de agua el miércoles, ¿cuál es la capacidad máxima del depósito?.
Actividades en las que practicarás el cálculo de encadenamientos de aumentos y disminuciones porcentuales.
|
Problemas: Encadenamiento porcentual 1. El precio de un libro, 12 €, primero sube el 5 %, después sube el 10 % y, finalmente, baja el 15 %. a) ¿Cuál es su precio final? ¿Es igual que el inicial? b) ¿Cúal es el índice de variación total, y a qué porcentaje de aumento o de disminución corresponde?Solución: a) 11,78 €. No b) I.V. = 0,98175, entonces una disminución o descuento del 1,825 %
2. Según un artículo de un periódico, a unos trabajadores en el año 2002 se les sube el sueldo un 2%, en el 2003 el 3%, en el 2004 el 4% y los dos siguientes el 1%. ¿Es cierta la afirmación que en los 5 últimos años, a los trabajadores se les ha subido el sueldo un 2 + 3 + 4 + 1 + 1 = 11%?
Solución: No, pués el índice de variación total = 1,02 . 1,03 . 1,04 . 1,01 . 1,01 = 1,1146, es decir un aumento del 11,46% |
Ejercicios y problemas
Problemas con porcentajes.
Practica distintos problemas de porcentajes.
Problemas con porcentajes de diversos tipos.
Problemas de aumentos y disminuciones porcentuales de diversos tipos.
Autoevaluación sobre porcentajes.
Autoevaluación sobre problemas con porcentajes.
Autoevaluación sobre problemas de aumentos porcentuales y comisiones.
Problemas de autoevaluación sobre porcentajes.
Problemas resueltos sobre porcentajes.