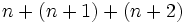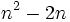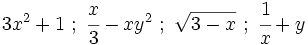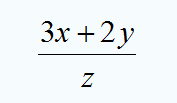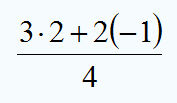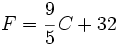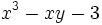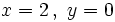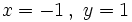Expresiones algebraicas (3ºESO Académicas)
De Wikipedia
| Revisión de 18:40 28 may 2017 Coordinador (Discusión | contribuciones) (→Tipos de expresiones algebraicas) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| __TOC__ | __TOC__ | ||
| + | {{p}} | ||
| + | {{Cita: la belleza del álgebra}} | ||
| + | {{p}} | ||
| + | ==Introducción== | ||
| + | {{Introducción : expresiones algebraicas}} | ||
| + | |||
| + | {{Introducción: Utilidad del álgebra}} | ||
| {{p}} | {{p}} | ||
| (Pág. 84) | (Pág. 84) | ||
| + | |||
| + | ==El lenguaje algebraico== | ||
| + | {{Uso de letras en lugar de números}} | ||
| + | {{p}} | ||
| + | |||
| ==Expresiones algebraicas== | ==Expresiones algebraicas== | ||
| {{expresiones algebraicas}} | {{expresiones algebraicas}} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Tipos de expresiones algebraicas== | ==Tipos de expresiones algebraicas== | ||
| {{tipos de expresiones algebraicas}} | {{tipos de expresiones algebraicas}} | ||
| Línea 38: | Línea 51: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Expresiones algebraicas|enunciado= | ||
| - | {{Video_enlace_carreon | ||
| - | |titulo1=Ejemplos 1: Expresiones algebraicas | ||
| - | |duracion=3'43" | ||
| - | |sinopsis=Como se traducen expresiones del lenguaje cotidiano a expresiones algebraicas y su uso en el planteamiento de ecuaciones. | ||
| - | |url1=https://www.youtube.com/watch?v=BeNb5En9LeI&list=PLDjtbBXUusIxoU4YE4pbHYwXNFfVWexD7 | ||
| - | }} | ||
| - | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejemplos 2: Expresiones algebraicas | ||
| - | |duracion=16'35" | ||
| - | |sinopsis=Como se traducen expresiones del lenguaje cotidiano a expresiones algebraicas y su uso en el planteamiento de ecuaciones. | ||
| - | |url1=https://www.youtube.com/watch?v=EYG1XvNUZF0 | ||
| - | }} | ||
| - | }} | ||
| ==Valor numérico de una expresión algebraica== | ==Valor numérico de una expresión algebraica== | ||
| {{Valor numérico de una expresión algebraica}} | {{Valor numérico de una expresión algebraica}} | ||
| {{p}} | {{p}} | ||
| - | ==Ejercicios propuestos== | + | ==Ejercicios== |
| + | {{Ejercicios: Expresiones algebraicas}} | ||
| + | |||
| + | ===Ejercicios propuestos=== | ||
| {{ejercicio | {{ejercicio | ||
| |titulo=Ejercicios propuestos: ''Expresiones algebraicas'' | |titulo=Ejercicios propuestos: ''Expresiones algebraicas'' | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
| "La Filosofía está escrita en ese grandísimo libro abierto ante nuestros ojos; quiero decir, el Universo; pero no se puede entender si antes no aprendemos su lenguaje y distinguimos los símbolos en el que está escrito. Este libro está escrito en el lenguaje de las matemáticas ... sin las cuales uno deambula vanamente en un obscuro laberinto." |
Introducción
Hasta ahora nos ha bastado con utilizar números (enteros, fracciones, decimales...) y operaciones entre ellos para resolver multitud de problemas. Sin embargo, el lenguaje matemático no puede limitarse a números y operaciones. En muchas ocasiones necesitaremos pasar de lo concreto a lo general (abstracción) para intentar resolver no sólo un problema, sino un conjunto de problemas del mismo tipo. Muchas situaciones requieren manejar una infinidad de números al mismo tiempo, y como mencionarlos a todos, uno a uno, no es una opción, necesitamos una herramienta que nos facilite la tarea.
El concepto de abstracción está inmerso en nuestra vida diaria cuando utilizamos palabras o símbolos para referirnos a los objetos que nos rodean.

Los primeros matemáticos que intentaron describir métodos generales para la resolución de problemas se apoyaron en el lenguaje convencional. La idea era redactar los pasos para la solución de un problema utilizando las palabras del idioma propio. Fíjate en el siguiente extracto de una traducción del Libro del Álgebra, escrito por el matemático Muhammad ibn Musa al-Jwarizmi, que vivió entre finales del siglo VIII y comienzos del siglo IX:
|
"Un hombre muere y deja dos hijos, y lega a un amigo un tercio del capital. Y deja diez dirhams de capital y una deuda de diez dirhams a uno de sus hijos. La solución está en tomar como cosa lo extraído de la deuda, y lo sumamos sobre el capital (que es diez dirhams), y tenemos diez más la cosa. Después pones aparte un tercio (porque legó un tercio de su capital), que es tres dirhams más un tercio más un tercio de la cosa..." |
El fragmento está incompleto, pero más allá de eso, resulta difícil seguir su explicación, pese a que el objetivo de la obra era facilitar la transmisión de los métodos de resolución de problemas conocidos en la época. Sí puedes apreciar que utiliza varias veces la palabra "cosa" para referirse a lo que se quiere calcular. Es lo que nosotros llamamos en la actualidad incógnita o variable. Esta obra fue uno de los primeros pasos en la creación del lenguaje algebraico, que ha cambiado mucho a lo largo del tiempo, hasta llegar a lo que es hoy en día, un lenguaje universal (no depende de traducciones, es igual en cualquier parte del mundo) y conciso (elimina todos lo elementos superfluos, propios del lenguaje habitual, y se centra en los elementos necesarios para resolver el problema que corresponda).
Un poco de historia sobre los orígenes del álgebra.
Es difícil definir el lenguaje algebraico con pocas palabras. Podríamos decir, por ejemplo, que es el conjunto de símbolos y reglas que se utilizan para la transmisión de ideas matemáticas. Es una definición demasiado amplia, pero lo que realmente nos interesa es aprender a usarlo. Muchos de esos símbolos y reglas ya los conoces (los números, el orden de las operaciones, las propiedades de las operaciones, ...) y otros los estudiaremos en breve (monomios, polinomios, operaciones con polinomios, ...). (Extraido de aquí)
La forma más sencilla de entender el álgebra.
Empecemos el tema con un toque divertido:
Troncho y Poncho nos explican las expresiones algebraicas y las ecuaciones.
Puedes encontrar ejercicios sobre este vídeo y material similar en: http://www.angelitoons.com/
- Averigua el valor de cada una de las letras que aparecen en la escena.
- El sistema de numeración romano utilizaba letras para representar números. Aquí podrás recordarlo.
(Pág. 84)
El lenguaje algebraico
Muchas veces, las Matemáticas requieren trabajar con números cuyo valor es desconocido o variable. En tales casos, los números se representan mediante letras y se operan con ellas utilizando las mismas reglas que cuando trabajamos con números. Estamos traduciendo al "lenguaje de las Matemáticas".
Llamaremos lenguaje algebraico al conjunto de símbolos (números, letras, símbolos de operación) y reglas que se utilizan para la transmisión de ideas matemáticas. De su estudio se encarga la parte de las matemáticas denominada álgebra.
Cómo se traduce al lenguaje algebraico
Al pasar del lenguaje convencional al lenguaje algebraico, debemos tener en cuenta algunas cosas:
- Los elementos desconocidos o aquellos que no tienen un valor fijo (variables) se representan mediante letras, mientras que aquellos que tienen su valor completamente determinado (constantes) se suelen expresar con números.
- Si un enunciado habla de dos números que pueden ser diferentes, es necesario usar una letra distinta para cada uno. Cuando una letra aparece repetida en un mismo enunciado, se entiende que son varias referencias a un mismo número.
- Las relaciones entre números y variables se expresan mediante operaciones matemáticas.
¿Qué es una variable?
¿Para qué todas esas letras en álgebra?
¿Por qué no usamos el signo de multiplicación al escribir variables?
Veamos algunas situaciones en la que resulta conveniente recurrir al lenguaje algebraico:
- Expresión de propiedades o reglas
Por ejemplo, la propiedad conmutativa del producto de dos números dice que "el orden de los factores no altera el producto". Ésto lo podemos expresar usando letras, de la siguiente manera:
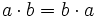
La regla de la división dice que "el dividendo es igual al divisor por el cociente más el resto". Ésto lo podemos expresar usando letras, de la siguiente manera:
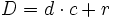
- Expresión de fórmulas
Por ejemplo, la fórmula del área del triángulo dice que "el área de un triángulo es igual a la base por la altura partido por 2", que podemos expresar con letras:
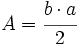
- Generalización de relaciones numéricas
Si consideramos la siguiente sucesión numérica
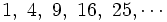
la expresión 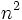 sirve para generalizar sus términos, de manera que, si yo quiero obtener el término que ocupa el séptimo lugar, tan solo tendré que sustituir la letra
sirve para generalizar sus términos, de manera que, si yo quiero obtener el término que ocupa el séptimo lugar, tan solo tendré que sustituir la letra  por el número 7,
por el número 7,
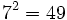
- Expresión de números desconocidos y planteamiento de ecuaciones
Por ejemplo, "la suma de dos números consecutivos es igual a 21" lo podemos expresar
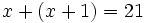
donde estamos utilizando la letra  para representar al primer número y la expresión
para representar al primer número y la expresión 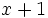 para representar al segundo número.
para representar al segundo número.
Ejercicio resuelto: Traducir al lenguaje algebraico
Traduce al lenguaje algebraico las siguientes expresiones del lenguaje habitual:
- a) El doble de un número menos cuatro unidades.
- b) La mitad de sumarle 5 al triple de un número.
- c) El perímetro y el área de un terreno rectangular.
a) Si llamamos  al número, entonces el doble del número menos cuatro unidades es
al número, entonces el doble del número menos cuatro unidades es 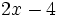 .
.
b) Llamando  al número, la mitad de sumarle 5 al triple de dicho número es
al número, la mitad de sumarle 5 al triple de dicho número es 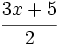
c) Si suponemos que el terreno rectangular mide  de largo e
de largo e  de ancho, tenemos:
de ancho, tenemos:
- Perimetro:
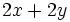
- Area:
"La Filosofía está escrita en ese grandísimo libro abierto ante nuestros ojos; quiero decir, el Universo; pero no se puede entender si antes no aprendemos su lenguaje y distinguimos los símbolos en el que está escrito. este libro está escrito en el lenguaje de las matemáticas ... sin las cuales uno deambula vanamente en un obscuro laberinto." (Galileo Galilei) Paso de lenguaje habitual a lenguaje algebraico y viceversa. Vamos a ver la diferencia entre el lenguaje aritmético y el lenguaje algebraico Cómo se traducen expresiones del lenguaje cotidiano al lenguaje algebraico y su uso en el planteamiento de ecuaciones. | Cómo se traducen expresiones del lenguaje cotidiano al lenguaje algebraico. Cómo se traducen expresiones del lenguaje cotidiano al lenguaje algebraico. Letras en lugar de números. El lenguaje algebraico es la base que te permitirá plantear ecuaciones para resolver problemas. Cómo se traducen expresiones del lenguaje cotidiano al lenguaje algebraico y su uso en el planteamiento de ecuaciones. |
Expresa en lenguaje algebraico:
Expresa en lenguaje algebraico:
Escribe en lenguaje algebraico: La mitad de un número más el cuadrado del mismo.Escribe en lenguaje algebraico: Un número más seis, menos 15, es igual al cuadrado de otro número.Escribe en lenguaje algebraico: La octava parte de un número es igual a un tercio de la suma de otros dos.Traduce al lenguaje algebraico los siguientes enunciados:
Escribe en lenguaje algebraico: Pablo tenía "x" dólares, cobró "m" dólares y le regalaron "z" dólares.¿Cuánto tiene Pablo?Escribe en lenguaje algebraico: Se compraron (m-1) vacas por 2000 dólares.¿Cuál es el precio de cada vaca?Escribe en lenguaje algebraico: Compré "n" sombreros por "x" dólares. ¿A cómo habría salido cada sombrero si hubiera comprado 2 sombreros menos por el mismo precio?Escribe en lenguaje algebraico: Tenía "x" dólares y me pagaron "n". Si el dinero que tengo lo empleo todo en comprar (m-1) libros, ¿a cómo sale cada libro?Escribe en lenguaje algebraico: José tiene "n" dólares; Juan tiene la tercera parte de la de José; Ana la cuarta parte del duplo de lo de José. la suma de lo que tienen los tres es menor que 3000 dólares. ¿Cuánto falta a esta suma para ser igual a 3000 dólares? | Escribe en lenguaje algebraico: La suma de tres números pares consecutivos es igual al triple del menor, más las tres cuartas partes del mayor.Escribe en lenguaje algebraico: ¿Cuál es el largo de un rectángulo, si se sabe que el largo es tres veces su ancho?Escribe en lenguaje algebraico: El doble de un número equivale al triple de su antecesor excedido en siete.Escribe en lenguaje algebraico: El cuadrado de la suma de dos números es igual a 49.Escribe en lenguaje algebraico: Las dos terceras partes de un número, más el triple de su consecutivo, menos su inverso equivale a 10.
El guapo Jack va a comprar un poni de diamantes. El poni cuesta P pesos, y Jack tienen que pagar un impuesto del 25% sobre los ponis de diamantes. Haz coincidir las expresiones dadas (ver video) con sus significados. Donovan come 2 barras de granola y un vaso de zumo de naranja como desayuno cada mañana. El precio de una barra de granola es B y el precio de un vaso de jugo es J. hay diferentes formas de expresar el coste del desayuno de Donovan durante una semana. Junta las expresiones dadas (ver video) con sus descripciones correspondientes. Escribe un enunciado para la siguiente expresión algebraica: Escribe un enunciado para la siguiente expresión algebraica: Sean "x", "y" y "z" números enteros:
|
Aprende a manejar expresiones algebraicas
Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico.
Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico.
Cómo escribir expresiones básicas con variables.
Cómo escribir expresiones con variables.
Problemas verbales sobre escritura de expresiones básicas.
Cómo escribir expresiones básicas con variables
Cómo escribir expresiones con variables
Problemas verbales sobre escritura de expresiones básicas.
Problemas verbales sobre escritura de expresiones.
Interpreta expresiones algebraicas.
Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico.
Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico.
Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico.
Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico.
Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico.
Expresiones algebraicas
- Una expresión algebraica es una combinación de letras y números ligados por las operaciones matemáticas (suma, resta, multiplicación, división, potenciación, radicación, ...), que respeta las reglas del lenguaje algebraico.
- Las letras, que suelen representar cantidades desconocidas, no tienen un valor fijo y se denominan variables. Los números se denominan constantes porque tienen un valor fijo.
- Se puede usar cualquier letra del alfabeto para expresar una variable, excepto la "e" y la "i", porque están reservadas para unos números especiales. Las letras más habituales son x, y, z, a, b, c, ...
- Las reglas que se mencionan en la definición son las mismas que ya teníamos en cuenta al trabajar únicamente con números y alguna otra que aparecerá más adelante. Entre ellas tenemos:
- Dos símbolos de operación no pueden aparecer juntos sin estar separados por otro elemento (paréntesis, corchetes, raya de fracción...)
- Cuando realizamos una operación combinada en varias etapas, cada una de ellas tiene que estar precedida del símbolo =, y los elementos que no se operan deben repetirse en la misma posición o en una equivalente, siempre respetando las propiedades de las operaciones.
- Si el símbolo = está seguido por una raya de fracción, ésta debe aparecer a una altura intermedia entre las dos rayas del igual.
- El número 1 puede omitirse cuando está multiplicando a otro número o cuando actúa como exponente.
- El símbolo de la multiplicación puede omitirse cuando a continuación del mismo aparecen unos paréntesis, o cuando se indica el producto de dos variables (letras).
- ...
Expresiones algebraicas: definición y ejemplos.
Expresiones algebraicas. Tipos de expresiones algebraicas: enteras y fraccionarias.
Indica si las siguientes expresiones algebraicas son enteras o fraccionarias:
- 44)
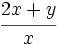 ; 45)
; 45) 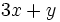 ; 46)
; 46) 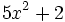
- 47)
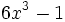 ; 48)
; 48) 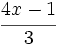 ; 49)
; 49) 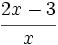
- 50)
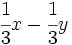
Ejemplos de expresiones algebraicas.
Actividad en la que deberás encontrar la expresión algebraica adecuada para cada situación.
Actividad en la que deberás encontrar la expresión algebraica adecuada para cada situación.
Tipos de expresiones algebraicas
Hay distintos tipos de expresiones algebraicas. Nosotros nos vamos a centrar, de manera especial, en unas que llamaremos monomios y polinomios.
- Monomio: es una expresión algebraica que consta de un número (coeficiente), multiplicado por letras (variables) con exponentes naturales.
- Polinomio: es la suma de varios monomios. Algunos polinomios tienen nombre propio: binomio (2 sumandos), trinomio (3 sumandos), ...
En general, cuando hablemos de polinomios, nos referiremos tanto a los monomios como a los polinomios. Es decir, un monomio lo veremos como un polinomio con un solo sumando.
- Monomios:
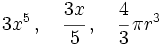
- Polinomios:
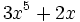 (binomio)
(binomio)
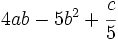 (trinomio)
(trinomio)
- No son monomios, ni polinomios:
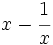 , porque la variable aparece dividiendo.
, porque la variable aparece dividiendo.
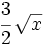 , porque la variable aparece dentro de una raíz.
, porque la variable aparece dentro de una raíz.
Elementos que componen una término algebraico.
Elementos que componen una expresión algebraica. Clasificación de las expresiones algebraicas.
Monomios, binomios, trinomios y polinomios. Ejemplos.
Actividad en la que deberás decir de qué tipo es la expresión algebraica dada.
Ejercicios resueltos:
Expresa algebraicamente:
- a) El perímetro de un rectángulo, uno de cuyos lados es el triple del otro, es 60 cm.
- b) Si gasto 3/5 de lo que tengo y, además, 90 €, me quedaré con la tercera parte de lo que tengo.
Solución a)
- Lado menor:
 (monomio)
(monomio)
- Lado mayor:
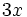 (monomio)
(monomio)
- Perímetro:
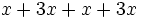 (polinomio)
(polinomio)
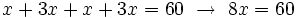 (ecuación)
(ecuación)Solución b)
- Dinero que tengo:
 (monomio)
(monomio)
- Gasto:
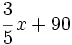 (polinomio)
(polinomio)
- Me queda:
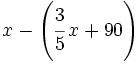 (polinomio)
(polinomio)
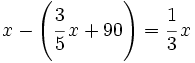 (ecuación)
(ecuación)Valor numérico de una expresión algebraica
| El lenguaje algebraico sirve para pasar de casos particulares a casos generales, sin embargo, en muchas ocasiones haremos el proceso inverso, pasaremos de una expresión general a un valor concreto.
Si en una expresión algebraica se sustituyen las letras (variables) por números y se realizan las operaciones correspondientes, se obtiene un número al que llamaremos el valor númerico de la expresión algebraica para los valores de las letras asignados. |
Ejemplo: Valor numérico de una expresión algebraica
Halla el valor numérico:
- a)
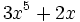 para
para 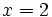
- b)
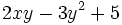 para
para 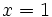 e
e 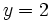 .
.
a) El valor numérico es: 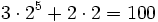
Tutorial en el que se explica y trabaja el cálculo del valor numérico de expresiones algebraicas de una o más variables, así como las tablas de valores.
En este video vamos a ver lo que es el valor numérico de una expresión algebraica y cómo se calcula.
Calcula el valor numérico de la expresión algebraica 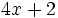 para
para 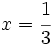 .
.
Calcula el valor numérico de la expresión algebraica 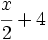 para
para 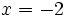 .
.
Calcula el valor numérico de la expresión algebraica 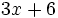 para
para 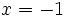 .
.
Calcula el valor numérico de la expresión algebraica 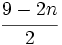 para
para 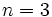 .
.
Calcula el valor numérico de la expresión algebraica 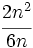 para
para 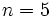 .
.
Calcula el valor numérico de la expresión algebraica 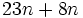 para
para 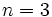 .
.
Calcula el valor numérico de la expresión algebraica 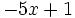 para
para 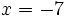 .
.
Calcula el valor numérico de las siguientes expresiones algebraicas para los valores indicados de las variables:
- 51)
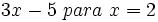
- 52)
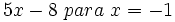
- 53)
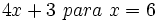
- 54)
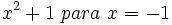
- 55)
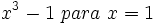
- 56)
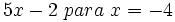
- 57)
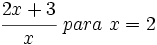
- 58)
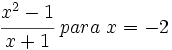
- 59)
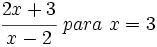
Un hospital local está realizando una rifa para recolectar fondos. El coste individual para participar en la rifa está dado por la expresión 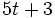 , donde
, donde 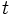 representa el número de boletos que la persona adquiere. Evalúa la expresión para
representa el número de boletos que la persona adquiere. Evalúa la expresión para 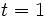 ,
, 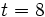 y
y 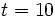 .
.
- a) Evalúa la expresión
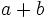 para
para 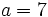 y
y 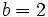 .
.
- b) Evalúa la expresión
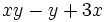 para
para  e
e 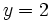 .
.
- a) Evalúa la expresión
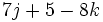 para
para 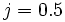 y
y 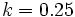 .
.
- b) Evalúa la expresión
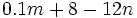 para
para 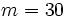 y
y  .
.
- a) ¿Qué le ocurre a la expresión
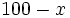 cuando la variable
cuando la variable  va disminuyendo?
va disminuyendo?
- b) ¿Qué le ocurre a la expresión
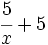 cuando la variable
cuando la variable  va disminuyendo, pero manteniéndose positiva?
va disminuyendo, pero manteniéndose positiva?
Expresa 25º Celsius (C) como una temperatura en grados Fahrenheit (F), usando la fórmula:
El área de la superficie de un cubo es igual a la suma de las áreas de sus 6 caras. En consecuencia, vendrá dada por la fórmula 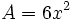 , siendo
, siendo  el valor de la arista del cubo.
el valor de la arista del cubo.
Julia tiene dos recipientes de forma cúbica que quiere pintar. Uno tiene arista 2 y otro 1.5. Calcula el área total que quiere pintar.
Evalúa la expresión 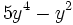 cuando
cuando 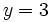 .
.
Actividades en la que aprenderás y practicarás el cálculo del valor numérico de una expresión algebraica.
Actividades en la que aprenderás y practicarás el cálculo del valor numérico de una expresión algebraica.
Evaluar expresiones con una sola variable.
Evaluar expresiones con dos variables.
Evaluar expresiones con dos variables: fracciones y decimales.
Intuición sobre el valor de una expresión.
Intuición sobre el valor de una expresión.
Evaluar expresiones con variables: problemas verbales.
Evaluar expresiones con una sola variable.
Evaluar expresiones con múltiples variables.
Evaluar expresiones con múltiples variables: fracciones y decimales.
Intuición sobre el valor de una expresión.
Evaluar expresiones con variables: problemas verbales.
Evaluar expresiones con potencias.
Autoevaluación sobre el valor numérico de una expresión algebraica.
Ejercicios
Teoría y actividades sobre expresiones algebraicas: monomios, polinomios, operaciones.
Ejercicios de autoevaluación sobre expresiones algebraicas y valor numérico.
Ejercicios propuestos
|
Ejercicios propuestos: Expresiones algebraicas |