Plantilla:Sucesivas ampliaciones de los conjuntos numericos
De Wikipedia
| Revisión de 10:28 24 nov 2017 Coordinador (Discusión | contribuciones) (→Números naturales) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Números racionales) |
||
| Línea 3: | Línea 3: | ||
| {{Def cto num naturales}} | {{Def cto num naturales}} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace_fonemato | + | {{Video: Historia del cero}} |
| - | |titulo1=La facultad de abstracción. Historia del cero | + | |
| - | |duracion=2'42" | + | |
| - | |sinopsis=Toda abstracción es en sí misma una fuente de contradicciones: su depuración es larga y difícil, pues las ideas siempre tardan en madurar. | + | |
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/04-la-facultad-de-abstraccion-historia-del-cero-6#.VCVYPhZ8HA8 | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace_fonemato | + | |
| - | |titulo1=Prohibido dividir por cero | + | |
| - | |duracion=5'58" | + | |
| - | |sinopsis=Todo cociente de números cuyo denominador sea 0 carece de sentido matemático. | + | |
| - | De otro modo: si se admite la división por "cero" es el caos, pues entonces 2 = 1. Por eso,si divides por cero, aunque sea sin darte cuenta, serás fusilado de inmediato y expulsado de la comunidad científica por los siglos de los siglos. | + | |
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/05-prohibido-dividir-por-cero-4#.VCVbhhZ8HA8 | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| Este conjunto es insuficiente si queremos dar solución a ecuaciones como: | Este conjunto es insuficiente si queremos dar solución a ecuaciones como: | ||
| Línea 23: | Línea 10: | ||
| {{p}} | {{p}} | ||
| Se precisa de un conjunto más amplio que incluya a los números negativos, el conjunto de los números enteros. | Se precisa de un conjunto más amplio que incluya a los números negativos, el conjunto de los números enteros. | ||
| - | ---- | + | {{p}} |
| - | Para más información: [[Números naturales]] | + | {{Info|texto=Para más información: [[Números naturales]]}} |
| + | {{p}} | ||
| ===Números enteros=== | ===Números enteros=== | ||
| Línea 34: | Línea 22: | ||
| no tiene solución en el conjunto de los números enteros ya que requiere números fraccionarios. Es necesaria la ampliación al conjunto de los números racionales. | no tiene solución en el conjunto de los números enteros ya que requiere números fraccionarios. Es necesaria la ampliación al conjunto de los números racionales. | ||
| + | {{p}} | ||
| + | {{Info|texto=Para más información: [[Números enteros]]}} | ||
| + | {{p}} | ||
| ===Números racionales=== | ===Números racionales=== | ||
| - | {{Tabla75 | + | {{el conjunto de los números racionales}} |
| - | |celda2=[[Image:cto_racionales.png|right|200px]] | + | |
| - | |celda1= | + | |
| - | {{def cto racionales}} | + | |
| {{p}} | {{p}} | ||
| - | Estos números, o bien son enteros, o bien se pueden expresar mediante decimales exactos o periódicos. | + | {{Prohibido dividir por cero}} |
| + | {{p}} | ||
| + | {{Info|texto=Para más información: [[Números racionales]]}} | ||
| {{p}} | {{p}} | ||
| Pero, ¿qué ocurre si queremos resolver la siguiente ecuación?: | Pero, ¿qué ocurre si queremos resolver la siguiente ecuación?: | ||
| Línea 48: | Línea 38: | ||
| {{p}} | {{p}} | ||
| La respuesta la tienes en el siguiente resultado: | La respuesta la tienes en el siguiente resultado: | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| {{Raiz de 2 no es racional}} | {{Raiz de 2 no es racional}} | ||
| Línea 55: | Línea 44: | ||
| {{p}} | {{p}} | ||
| {{Raiz de primo es irracional}} | {{Raiz de primo es irracional}} | ||
| - | {{p}}{{p}} | ||
| - | {{Teorema|titulo=Propiedades|enunciado= | ||
| - | *La suma de un racional y un irracional es otro irracional | ||
| - | |||
| - | *El producto de un racional por un irracional es otro irracional. | ||
| - | |||
| - | *Existe al menos un irracional entre cualesquiera dos racionales. | ||
| - | |demo= | ||
| - | {{Video_enlace | ||
| - | |titulo1=La suma de un racional y un irracional es otro irracional | ||
| - | |duracion=6´51" | ||
| - | |sinopsis=La demostración, en este videotutorial. | ||
| - | |url1=https://www.youtube.com/watch?v=NSJN3oW6mm4 | ||
| - | }} | ||
| - | |||
| - | {{Video_enlace | ||
| - | |titulo1=El producto de un racional por un irracional es otro irracional | ||
| - | |duracion=5´23" | ||
| - | |sinopsis=La demostración, en este videotutorial. | ||
| - | |url1=https://www.youtube.com/watch?v=VooyYyUdmS4 | ||
| - | }} | ||
| - | |||
| - | {{Video_enlace | ||
| - | |titulo1=Existe al menos un irracional entre cualesquiera dos racionales | ||
| - | |duracion=7´48" | ||
| - | |sinopsis=La demostración, en este videotutorial. | ||
| - | |url1=https://www.youtube.com/watch?v=r2VhbOxjUhQ | ||
| - | }} | ||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | {{p}} | ||
| {{p}} | {{p}} | ||
| Surge, por tanto, la necesidad de ampliar el conjunto de los números racionales, añadiendole estos nuevos números que llamaremos [[números irracionales]]. | Surge, por tanto, la necesidad de ampliar el conjunto de los números racionales, añadiendole estos nuevos números que llamaremos [[números irracionales]]. | ||
| Línea 97: | Línea 53: | ||
| {{p}} | {{p}} | ||
| {{irracionales_famosos}} | {{irracionales_famosos}} | ||
| + | {{p}} | ||
| + | {{Propiedades irracionales}} | ||
| + | {{p}} | ||
| + | {{Info|texto=Para más información: [[Números irracionales]]}} | ||
| + | {{p}} | ||
Revisión actual
Recordemos las sucesivas ampliaciones de los conjuntos númericos que se han estudiado en cursos anteriores:
Tabla de contenidos |
Números naturales
El conjunto de los números naturales es:
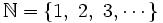
Se trata de un conjunto con infinitos elementos y sirven para:
- Contar (números cardinales: 1, 2, 3, ...).
- Ordenar (números ordinales: 1º, 2º, 3º, ...).
- Identificar y diferenciar los distintos elementos de un conjunto.
Puesto que los números naturales se utilizan para contar elementos, el cero (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero.
Veamos distintos ejemplos de uso de los números naturales:
- Como número cardinal: Los días de la semana son 7.
- Como número ordinal: El atleta británico quedó 3º en la prueba de cien metros lisos.
- Como identificador: Tú número de carnet de socio del Atleti es el 2868.
El conjunto de los números naturales: origen y definición.
El conjunto de los números naturales: origen y definición.
Tutorial de introducción al tema:
- Números naturales.
- Sistemas de numeración.
- Sistema de numeración decimal.
Hace unas horas tenía 16 años y el año que viene cumpliré 19. ¿Cómo explicas esta situación?
Ejercicios de autoevaluación sobre números naturales.
Existen dos teorías sobre el origen de la numeración, que además está relacionada con la cuestión de qué números aparecieron primero, los cardinales (1, 2, 3,...) o los ordinales (1º, 2º, 3º,...) La teoría que genera más consenso defiende el argumento de la necesidad. Todo habría comenzado a causa de la necesidad de contar objetos; por ello se habrían creado primero los números cardinales y después, los ordinales.
La otra teoría defiende la base espiritual de los números, que habrían tenido un uso ritual: cierto tipo de ceremonias requerían que los participantes se desplazaran o se situaran en un orden ritual preestablecido; por eso los números ordinales serían anteriores a los cardinales. Esta teoría además postula que los números se originaron en un lugar geográfico determinado, desde el que se propagaron al resto del mundo; también establece la división de los números naturales en pares e impares, considerando los impares masculinos y los pares, femeninos, una clasificación que comparten hoy en día muchas culturas del planeta.
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 10)"
Véanse los artículos de la BBC:
- ¿Sabes que el 1 y el 2 no son del mismo género y que los números tienen personalidades?
- Lo que quizás no sabías de los números
Toda abstracción es en sí misma una fuente de contradicciones: su depuración es larga y difícil, pues las ideas siempre tardan en madurar.
Este conjunto es insuficiente si queremos dar solución a ecuaciones como:
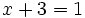
Se precisa de un conjunto más amplio que incluya a los números negativos, el conjunto de los números enteros.
Números enteros
Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor hay que restarle uno mayor. Nos vemos obligados a ampliar el concepto de números naturales, introduciendo un nuevo conjunto numérico llamado números enteros.
El conjunto de los números enteros
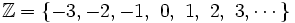
Está formado por:
- El conjunto de los números naturales o enteros positivos :
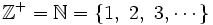 .
.
- Sus opuestos, los enteros negativos:
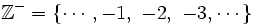 .
.
- El cero (0).
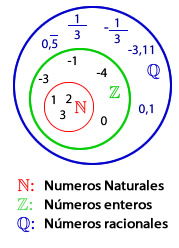
Como consecuencia, 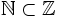 , que se lee: "el conjunto de los números naturales está incluido en el conjunto de los números enteros".
, que se lee: "el conjunto de los números naturales está incluido en el conjunto de los números enteros".
Los números enteros: utilidad y definición.
Los números enteros: utilidad y definición.
En este video vamos a ver lo que son los números enteros y también las clases de números enteros que hay, es decir, números enteros positivos y números enteros negativos, además del cero.
El conjunto de los números enteros. El subconjunto de los números enteros positivos, el de los negativos y el cero. Representación y notación.
El conjunto de los números enteros. Utilidad. Representación y operaciones en la recta numérica.
Las criaturas o entes llamados números no exixten realmente: nadie ha visto jamás un número, ya sea famoso (como el representado por el símolo 5 y llamado cinco) o no. Los números sólo exixten a la luz de la inteligencia humana. Existen en la medida en que nos son útiles. Los Números Naturales son todos enteros y positivos. Son muy útiles para contar, pero tienen sus limitaciones, de manera que hubo que inventar otro tipo de números...
Number systems evolved from the natural "counting" numbers, to whole numbers (with the addition of zero), to integers (with the addition of negative numbers), and beyond. These number systems are easily understood using the number line.
(Disponibles los subtítulos en inglés)
Utilidad de números negativos en la vida real. El conjunto de los números enteros. Representación en la recta numérica.
Este conjunto también se nos queda chico. Por ejemplo, la ecuación
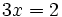
no tiene solución en el conjunto de los números enteros ya que requiere números fraccionarios. Es necesaria la ampliación al conjunto de los números racionales.
Números racionales
El conjunto de los números racionales es el conjunto de todas las fracciones: 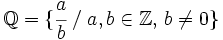 Obseva que:
Proposición La suma y el producto de dos números racionales es otro número racional. Demostración: Demostración de que la suma y el producto de dos racionales es racional. El conjunto de los números racionales El conjunto de los números racionales El conjunto de los números racionales. Introducción a números racionales e irracionales. |
Todo cociente de números cuyo denominador sea 0 carece de sentido matemático. De otro modo: si se admite la división por "cero" es el caos, pues entonces 2 = 1. Por eso,si divides por cero, aunque sea sin darte cuenta, serás fusilado de inmediato y expulsado de la comunidad científica por los siglos de los siglos.
¿Dónde está el error?
Pero, ¿qué ocurre si queremos resolver la siguiente ecuación?:
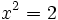
La respuesta la tienes en el siguiente resultado:
Proposición
No existe ningún número racional que elevado al cuadrado dé como resultado 2. Es decir, el número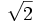 no es racional.
no es racional.
Demostración:
Vamos ha utilizar un tipo de demostración denominado "por reducción al absurdo". Supondremos que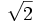 es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida.
es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida.
Por tanto, supongamos que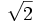 es racional, o sea, que existe una fracción que es igual a
es racional, o sea, que existe una fracción que es igual a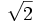 .
.
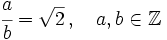
Elevamos al cuadrado los dos miembros de la igualdad:
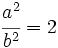
Multiplicamos por 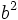 los dos miembros de la igualdad:
los dos miembros de la igualdad:
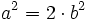 [1]
[1]Sabemos que en la descomposición factorial de un cuadrado perfecto, distinto de 1, todos los factores que aparecen lo hacen un número par de veces.
Como 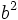 es un cuadrado perfecto, el factor 2 o no aparece o lo hace un número par de veces. Entonces, por la expresión [1], el factor 2 aparecería un número impar de veces en la descomposición del cuadrado perfecto
es un cuadrado perfecto, el factor 2 o no aparece o lo hace un número par de veces. Entonces, por la expresión [1], el factor 2 aparecería un número impar de veces en la descomposición del cuadrado perfecto 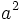 , lo cual no es posible.
, lo cual no es posible.
Ya hemos llegado al absurdo.
Tambián puedes ver la demostración en el siguiente videotutorial:
Videotutorial con otra demostración de la irracionalidad de la raíz de 2.
Videotutorial con la misma demostración que el video e Khan, pero más rápida y con un poco de historia.
Una breve historia de un número cuyo cuadrado es 2.
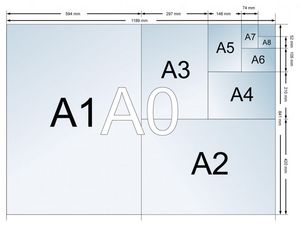
¡La de matemáticas que hay en un folio! ¿Sabes de dónde proviene el formato de hojas A4?.
No es necesario estar vinculado al sector de las Artes Gráficas o al mundo del diseño para estar en contacto diario con el sistema de clasificación o medidas de papel DIN A. Seguramente si alguna vez habrás tenido que imprimir un documento o imagen en un tamaño en concreto. Y en algún momento nos hemos preguntado si nuestra impresora podría tolerar ese tamaño de impresión. Estamos habituados a escuchar que si tal o cual formato está en A4, A3, A5, etc. ¿pero de qué manera funcionan todos? ¿cuál es su origen y sus utilidades? A continuación respondemos a estas preguntas.
DIN no es más que un acrónimo que significa Deutches Institut für Normung, que traducido significa Instituto Alemán de Normalización. Esta entidad que surgió en 1917 es la encargada de dictar los estándares o normas técnicas en Alemania. Dichas normas tienen como finalidad exclusiva asegurar y garantizar la calidad de aquello que se quiere normalizar, en este caso el tamaño del papel. Aunque quizás pienses que la normativa DIN sólo hace referencia al formato del papel, lo cierto es que existen y puedes encontrar aproximadamente 30.000 normativas DIN en este 2016 según archivo.
Fue el ingeniero berlinés Walter Porstmann quien estableció hacia el año 1922 las medidas DIN A a partir de la incorporación de la normativa DIN 476. El propósito era estandarizar de alguna manera los diferentes formatos de papel o página para aprovechar el máximo de papel y que hubiera el mínimo desperdicio posible. Dentro de la misma normativa DIN 476 encontramos la serie A, donde se definen precisamente estas medidas. Junto a la serie A también existen otras cuatro plantillas B, C, D y E y cada una de ellas contiene una numeración de varios tamaños: 0, 1, 2, 3, 4, 5, etc.
Las medidas DIN A parten de un formato referente que es el A0. El resto de formatos y series se calculan siempre a partir de éste.
En la serie A, al tamaño de papel de 1 m2 se le llama A0. Las divisiones posteriores que disminuyen la superficie a la mitad, reciben el nombre de A1, A2, A3, A4, etc. Lo que en realidad está indicando la numeración asociada a la letra A es la cantidad de cortes a la mitad desde la hoja original. Así por ejemplo, una hoja tamaño A4 tiene una superficie igual a la mitad de una hoja medida A3.
Cuando se corta por la mitad una hoja en tamaño A0 (1 m2), el lado más corto se convierte en la parte más larga de la hoja resultante (A1). Por tanto, si cortamos cualquier hoja de la serie a la mitad de su lado más largo, obtendremos siempre dos hojas del tamaño siguiente, que al mismo tiempo mantienen perfectamente las proporciones entre el ancho y el largo, siendo la razón de proporcionalidad igual a la raíz cuadrada de 2. Es decir, para cualquier formato DIN A, si dividimos el largo entre el ancho, nos dará (aproximadamente) 1,4142.
Puedes hacer la prueba: Mide el ancho y largo de una hoja tamaño DIN A4 y verás que se cumple la proporción; dóblala por el lado más largo y pártela por la mitad, mide el ancho y el largo de una de las mitades, divide las dos cifras y verás que se sigue cumpliendo: 1,4142.
Veamos la demostración:
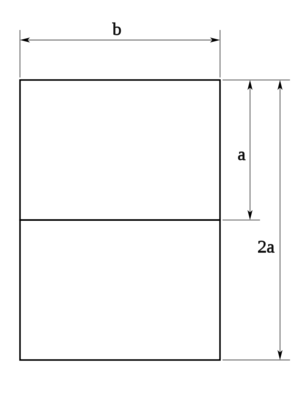
Partiendo de un formato de lados a y b, el formato superior tendrá 2a por b, para que la proporción entre sus lados sea la misma tendrá que cumplirse que:
Esto es:
Si la proporción entre el lado mayor y menor es raíz de dos, cortando un formato en dos iguales esta proporción se conserva.
Si el formato A0 tiene una superficie de un metro cuadrado, tendremos:
Sabiendo el valor de a el cálculo de b es inmediato:
Lo que podemos resumir como regla mnemotécnica que el formato DIN A0, tiene por medidas:
Dividiendo el lado mayor entre dos, obtendremos sucesivamente los distintos formatos A1, A2, A3, A4 ...
Exraido de: blog.imprentaonline24.es y wikipedia.es
De forma más general:
Proposición
Si 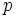 es un número primo, entonces el número
es un número primo, entonces el número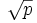 no es racional.
no es racional.
La demostración es análoga a la de que raíz de 2 es irracional.
Lo haremos, igualmente, "por reducción al absurdo". Supondremos que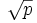 es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida.
es racional y llegaremos a una conclusión sin sentido, lo que demostrará la falsedad de la hipótesis de partida.
Por tanto, supongamos que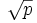 es racional, o sea, que existe una fracción que es igual a
es racional, o sea, que existe una fracción que es igual a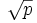 .
.
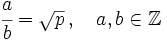
Elevamos al cuadrado los dos miembros de la igualdad:
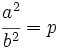
Multiplicamos por 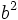 los dos miembros de la igualdad:
los dos miembros de la igualdad:
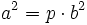 [1]
[1]Sabemos que en la descomposición factorial de un cuadrado perfecto, distinto de 1, todos los factores que aparecen lo hacen un número par de veces.
Como 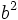 es un cuadrado perfecto, el factor
es un cuadrado perfecto, el factor 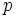 o no aparece o lo hace un número par de veces. Entonces, por la expresión [1], el factor primo
o no aparece o lo hace un número par de veces. Entonces, por la expresión [1], el factor primo 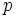 aparecería un número impar de veces en la descomposición del cuadrado perfecto
aparecería un número impar de veces en la descomposición del cuadrado perfecto 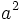 , lo cual no es posible.
, lo cual no es posible.
Ya hemos llegado al absurdo.
Videotutorial con otra demostración de la irracionalidad de la raíz de un número primo.
Surge, por tanto, la necesidad de ampliar el conjunto de los números racionales, añadiendole estos nuevos números que llamaremos números irracionales.
Números irracionales
El conjunto de los números irracionales es el formado por aquellos números que no se pueden expresar mediante fracciones y, por tanto, cuya expresión decimal tiene infinitas cifras no periódicas. Lo representaremos con la letra 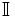 .
.
No existe una notación universal para representar al conjunto de los números irracionales, aunque la letra 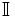 es generalmente aceptada. Una de las razones es que el conjunto de números irracionales no constituye estructura algebraica alguna, como ocurre con los naturales (
es generalmente aceptada. Una de las razones es que el conjunto de números irracionales no constituye estructura algebraica alguna, como ocurre con los naturales (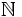 ), los enteros (
), los enteros (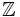 ), los racionales (
), los racionales (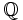 ), los reales (
), los reales (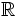 ) y los complejos (
) y los complejos (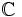 ). Por otro lado, está el hecho de que la
). Por otro lado, está el hecho de que la 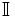 es tan apropiada para designar al conjunto de números irracionales como al conjunto de números imaginarios, lo cual puede crear confusión.
es tan apropiada para designar al conjunto de números irracionales como al conjunto de números imaginarios, lo cual puede crear confusión.
Son números irracionales:
- La raíces cuadradas no exactas de números enteros como
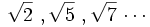
- Número famosos como el número pi, el número e o el número de oro Φ:
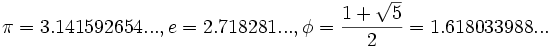
- Números con un patrón que no sea periódico: 5,123456789101112..., 8,12112111211112...
Aquí se habla un poco sobre algunos números extraños. Aunque no son tan extraños tampoco.
¿Cuáles de los siguientes números son irracionales?
¿Cuáles de los siguientes números son irracionales?
Actividades sobre números irracionales.
Clasifica en números racionales o irracionales.
Los números irracionales más famosos son los siguientes:
El número áureo, Phi:
¡Phi! El número dorado, la proporción divina... ¿Qué hace de éste número algo tan interesante? ¿Es cierto la sección áurea esconde el secreto del universo y la naturaleza? ¿Es mágica la proporción áurea?
El programa presenta a este exótico número ya conocido por los griegos. Veremos cómo se obtiene, qué son los rectángulos áureos y su presencia en infinidad de manifestaciones artísticas, en Pintura, Arquitectura, Escultura... a lo largo de la historia. Pero el número de oro no es un mero invento del hombre, la naturaleza nos sorprende de una forma que no puede ser casual, tanto en el mundo vegetal como en el animal, como en multitud de fenómenos físicos, con acontecimientos en los que este famosos número hace acto de presencia.
Documental sobre el número aureo.
La proporción áurea en el mundo que nos rodea y en el cuerpo humano como símbolo de belleza.
A lo largo de la historia, Phi, el número de oro o número áureo, ha representado, para las personas que lo han conocido, la belleza, la magia, la perfección, lo divino. ¿Por qué?. Página elaborada por D. Luis Nicolás Ortiz.
El número Pi:
El número Pi
Si las matemáticas tienen algún número emblemático ese es "pi" (π = 3,141592...). La figura de Ramanujan, un joven indio sin formación universitaria está intimamente ligada al número pi. A principio de siglo descubrió nuevas series infinitas para obtener valores aproximados de pi. Las mismas que utilizan los grandes ordenadores para obtener millones de cifras de este familiar y extraño número. Pero el verdadero padre de pi es un matemático griego de hace 2.300 años, Arquímedes. Él descubrió la famosa fórmula del área del círculo. Y también el volumen y el área de la esfera. De paso invento el primer método para obtener valores aproximados de pi aproximando el círculo mediante polígonos de un número creciente de lados.Pero pi no sólo aparece en matemáticas cuando se habla de círculos o esferas, su presencia en relaciones numéricas, en el cálculo de probabilidades y hasta en estudios estadísticos la confieren una omnipresencia casi mágica.
Distintas formas de obtener aproximaciones del número pi.
¿Qué relación hay entre Albert Einstein, los ríos y el famoso número Pi? Hoy en Derivando te lo vamos a explicar. ¡Ah! Y te recomendamos ver este vídeo mientras tomas una taza de té, ya verá cómo lo entiendes mejor.
Una de las constantes matemáticas más importantes que genera fascinantes problemas: el número Pi.
Curiosidades de Pi y cómo aprenderse sus decimales.
El número e:
¿Qué tiene el número Pi que no tenga e?
Te explicamos uno de los más importantes números reales irracionales y trascendentes, base de los logaritmos neperianos.
Hay números que nos sorprenden por su tendencia a aparecer en las situaciones más inesperadas. ¿ Qué pueden tener en común los cables del tendido eléctrico, las cuentas bancarias, el desarrollo de una colonia de bacterias, la prueba del carbono 14 para datar restos orgánicos, las encuestas de población, la probabilidad de sacar 70 veces un número par al lanzar un dado 100 veces...? Aparentemente nada. Sin embargo en todas estas situaciones interviene un extraño número comprendido entre 2 y 3, que tiene infinitas cifras decimales y un origen un tanto exótico. Al igual que el más famoso número pi, los matemáticos le conocen mediante una letra. Es un número llamado e.
Propiedades
- La suma de un racional y un irracional es otro irracional
- El producto de un racional por un irracional es otro irracional.
- Existe al menos un irracional entre cualesquiera dos racionales.
La demostración, en este videotutorial.
La demostración, en este videotutorial.
La demostración, en este videotutorial.
Ejercicios sobre las propiedades de las operaciones con números irracionales.
Ejercicios sobre las propiedades de las operaciones con números irracionales.
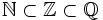
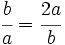
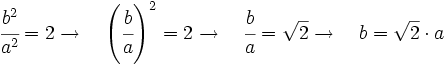
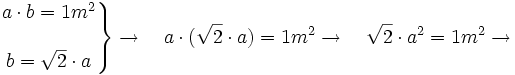
![a^2 = \cfrac{1m^2}{\sqrt{2}} \rightarrow \quad a = \sqrt{\cfrac{1m^2}{\sqrt{2}}} = \cfrac{1m}{\sqrt[4]{2}} = \cfrac{1}{1,189} \; m = 0,841 \; m](/wikipedia/images/math/e/d/6/ed67279193d5f651e1b3f739d1f96eb0.png)
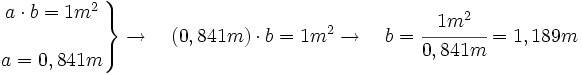
![DIN \; A0 \quad \left \{ \begin{matrix} ancho = \cfrac{1}{\sqrt[4]{2}} \; m \\ \\ largo = \sqrt[4]{2} \; m \end{matrix} \right .](/wikipedia/images/math/9/6/3/96380202caaa3fd258db9e669b1fa5c6.png)
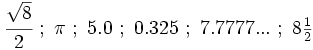
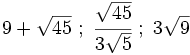
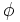 )
) 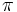 )
) 
