Números reales
De Wikipedia
| Revisión de 13:52 29 jul 2007 Coordinador (Discusión | contribuciones) (→Orden en el conjunto de los reales) ← Ir a diferencia anterior |
Revisión de 14:00 29 jul 2007 Coordinador (Discusión | contribuciones) (→Orden en el conjunto de los reales) Ir a siguiente diferencia → |
||
| Línea 36: | Línea 36: | ||
| ==Orden en el conjunto de los reales== | ==Orden en el conjunto de los reales== | ||
| {{Caja_Amarilla|texto=Dados dos números reales <math>a\;\!</math> y <math>b\;\!</math>, se dice que '''<math>a\;\!</math> es menor que <math>b\;\!</math>''', <math>(a<b)\;\!</math> si <math>b\;\!</math> está más a la derecha que <math>a\;\!</math> en la recta real. O dicho de otra forma, si <math>b-a\;\!</math> es positivo <math>(b-a>0)\;\!</math>}} | {{Caja_Amarilla|texto=Dados dos números reales <math>a\;\!</math> y <math>b\;\!</math>, se dice que '''<math>a\;\!</math> es menor que <math>b\;\!</math>''', <math>(a<b)\;\!</math> si <math>b\;\!</math> está más a la derecha que <math>a\;\!</math> en la recta real. O dicho de otra forma, si <math>b-a\;\!</math> es positivo <math>(b-a>0)\;\!</math>}} | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividad Interactiva: ''Orden en el conjunto de los reales''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1.''' Comparando dos números reales por su ubicación en la recta real. | ||
| + | |actividad= | ||
| + | {{p}} | ||
| + | Pulsa "inicio" para ver ejemplos. Fíjate que el punto rojo representa un número más pequeño que el punto azul. Mueve el punto rojo. Si los números se salen de pantalla, utiliza el zoom. | ||
| + | {{p}} | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros5_2.html | ||
| + | width=500 | ||
| + | height=200 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | }} | ||
| + | }} | ||
Revisión de 14:00 29 jul 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Números reales
Los números racionales y los irracionales forman el conjunto de los números reales y se designa con la letra 
Representación de los números reales
Cuando en una recta se representan los números racionales e irracionales se obtiene la recta real. Cualquier punto de la recta real representa un número real. .
|
Actividad Interactiva: Representación de los números reales
Actividad 1. Representación gráfica de los números reales en la recta real.
Actividad: Mueve el punto rojo y observa que todo punto de la recta representa un número real. Utiliza el zoom para ampliar la vista, si lo deseas. Luego introduce distintos número y observa su representación en la recta real:
|
Orden en el conjunto de los reales
Dados dos números reales  y
y  , se dice que
, se dice que  es menor que
es menor que  ,
, 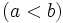 si
si  está más a la derecha que
está más a la derecha que  en la recta real. O dicho de otra forma, si
en la recta real. O dicho de otra forma, si 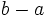 es positivo
es positivo 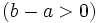
|
Actividad Interactiva: Orden en el conjunto de los reales
Actividad 1. Comparando dos números reales por su ubicación en la recta real.
Actividad: Pulsa "inicio" para ver ejemplos. Fíjate que el punto rojo representa un número más pequeño que el punto azul. Mueve el punto rojo. Si los números se salen de pantalla, utiliza el zoom. |
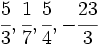 (teclea a/b para introducir la fracción
(teclea a/b para introducir la fracción  )
)

