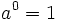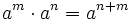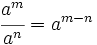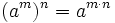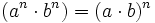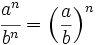Números Enteros (4ºESO-A)
De Wikipedia
| Revisión de 10:29 26 may 2008 Coordinador (Discusión | contribuciones) (→Orden en el conjunto de los enteros) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Menú Matemáticas 4ESOA | {{Menú Matemáticas 4ESOA | ||
| |ir= |ampliar= | |ir= |ampliar= | ||
| - | |repasar= | + | |repasar=[[Números enteros: Definición | Definiciones]]<br>[[Números enteros: Operaciones | Operaciones]] |
| - | |enlaces=[http://es.wikipedia.org/wiki/Numeros_naturales Números naturales] | + | |enlaces= |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Números enteros== | + | ==El conjunto de los números enteros== |
| {{Caja Amarilla|texto=El conjunto de los '''números enteros''' es | {{Caja Amarilla|texto=El conjunto de los '''números enteros''' es | ||
| - | <center><math>\mathbb{Z}=\left \lbrace \cdots, -3, -2,-1,\ 0,\ 1 ,\ 2,\ 3, \cdots \right \rbrace</math></center>}}{{p}}Son infinitos y, al igual que los [[números naturales]] sirven para contar. Sin embargo, los números enteros permiten expresar cantidades negativas como un saldo deudor en una cuenta bancaria, un año de la era antes de Cristo, el número de una planta del sótano de un edificio, etc. | + | <center><math>\mathbb{Z}=\left \lbrace \cdots, -3, -2,-1,\ 0,\ 1 ,\ 2,\ 3, \cdots \right \rbrace</math></center>}}{{p}}Son infinitos y, al igual que los números naturales sirven para contar. Sin embargo, los números enteros permiten expresar cantidades negativas como un saldo deudor en una cuenta bancaria, un año de la era antes de Cristo, el número de una planta del sótano de un edificio, etc. |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Números enteros''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1'''. Introducción al conjunto de los números enteros. | ||
| - | |actividad= | ||
| - | En la escena adjunta te presentamos unos ejemplos en los que se muestra la necesidad de utilizar números enteros. | ||
| - | Sigue las instrucciones que te van apareciendo en escena y anota los ejemplos en tu cuaderno. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/introduccionenteros_1.html | ||
| - | width=550 | ||
| - | height=550 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/introduccionenteros_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | }} | ||
| ==Representación de los números enteros== | ==Representación de los números enteros== | ||
| Línea 31: | Línea 15: | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: Representación de los números enteros''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1'''. Representación de los números enteros en la recta numérica. | ||
| - | |actividad= | ||
| - | En esta escena vas a conocer como se representan los números enteros en la recta numérica. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/rectanumerica_1.html | ||
| - | width=100% | ||
| - | height=500 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/rectanumerica_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | }} | ||
| ==Orden en el conjunto de los enteros== | ==Orden en el conjunto de los enteros== | ||
| En la [[Números enteros: Definición |representación de los enteros]] en la recta numérica se observa el orden que existe en el conjunto de los números enteros, siendo los números negativos menores que los positivos y que el cero.{{p}} | En la [[Números enteros: Definición |representación de los enteros]] en la recta numérica se observa el orden que existe en el conjunto de los números enteros, siendo los números negativos menores que los positivos y que el cero.{{p}} | ||
| Línea 51: | Línea 20: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas: ''Orden en los números enteros''|cuerpo= | + | ==Operaciones con enteros== |
| + | Las operaraciones con enteros son similares a las [[Números naturales: Operaciones | operaciones con naturales]], pero con las peculiaridades que aportan los números negativos. | ||
| + | ===Opuesto de un entero=== | ||
| + | El opuesto de un número entero <math>a\;\!</math> es otro número entero <math>-a\;\!</math>. | ||
| + | {{p}} | ||
| + | {{p}} | ||
| + | ===Suma y resta de enteros=== | ||
| + | La '''suma''' de números enteros es otro número entero. La '''resta''' de números enteros es otro número entero resultado de sumar el primero con el opuesto del segundo. | ||
| + | {{p}} | ||
| + | ===Jerarquía de las operaciones con enteros=== | ||
| + | Al operar con números enteros se atiende a la misma jerarquia de las operaciones con naturales. | ||
| + | {{Caja Amarilla|texto=Se efectúan primero el contenido de los '''paréntesis'''. De las operaciones, la de mayor prioridad es la '''potenciación''', seguida de la '''multiplicación''' y las '''división''' y, para terminar, la '''suma''' y la '''resta'''. | ||
| + | Si hay paréntesis anidados, se efectúan de dentro hacia fuera.}} | ||
| + | {{p}} | ||
| + | |||
| + | ===Multiplicación de enteros=== | ||
| + | Para multiplicar enteros usaremos la llamada '''regla de los signos''': | ||
| + | Si dos números enteros tienen el mismo signo su producto es un entero positivo. Y si tienen distinto signo, el producto es un entero negativo. Ésto es: | ||
| + | {{caja|contenido= | ||
| + | <center><math>(+) \cdot (+) = (+)</math></center> | ||
| + | <center><math>(-) \cdot (-) = (+)</math></center> | ||
| + | <center><math>(+) \cdot (-) = (-)</math></center> | ||
| + | <center><math>(-) \cdot (+) = (-)</math></center> | ||
| + | }}{{p}} | ||
| + | {{p}} | ||
| + | |||
| + | ===División de enteros=== | ||
| + | La división de números enteros, al igual que la división de números naturales, no siempre es otro entero. | ||
| + | Con la división , al igual que con la multiplicación, se aplica la misma regla de los signos. | ||
| + | |||
| + | {{caja|contenido= | ||
| + | <center><math>(+) : (+) = (+)\;\!</math></center> | ||
| + | <center><math>(-) : (-) = (+)\;\!</math></center> | ||
| + | <center><math>(+) : (-) = (-)\;\!</math></center> | ||
| + | <center><math>(-) : (+) = (-)\;\!</math></center> | ||
| + | }}{{p}} | ||
| + | |||
| + | {{AI2|titulo=Actividad Interactiva: ''Operaciones combinadas''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=1. ¿Cómo se ordenan los números enteros?. | + | |enunciado=1. Operaciones combinadas y con paréntesis: |
| |actividad= | |actividad= | ||
| - | En esta escena aprenderás a comparar números enteros. Anota lo que aprendas en tu cuaderno. | + | En esta actividad debes marcar en la ventana bajo la escena el número que sigue al resolver la expresión. Cuando el número marcado sea el correcto aparecerá en la escena, si no es el correcto no aparecerá. |
| - | Lee atentamente las indicaciones. Pulsa INICIO cada vez que quieras ver un ejemplo nuevo. | + | Debes hacerlo sucesivamente, paso a paso, para ello debes borrar el número anterior. No se trata de que halles directamente el resultado final. |
| + | Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. | ||
| + | |||
| + | {{Caja|contenido=<iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enteros2/opcombin_1.html | ||
| + | width=450 | ||
| + | height=350 | ||
| + | name=myframe | ||
| + | </iframe> | ||
| + | <center>[http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enteros2/opcombin_1.html '''Click''' aquí si no se ve bien la escena]</center>}} | ||
| + | }} | ||
| + | }} | ||
| + | ===Potencias de enteros=== | ||
| + | Las potencias de enteros cumplen las mismas propiedades que las potencias de números naturales. | ||
| + | {{Caja Amarilla|texto='''Potencia de base negativa:'''<br> | ||
| + | Al elevar un número negativo a una potencia, el resultado es positivo si el exponente es par y negativo si es impar. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/ordenenz_1.html | + | url=http://maralboran.org/web_ma/descartes/3_eso/Potencias_mac/potencias1_1.html |
| - | width=100% | + | width=630 |
| - | height=525 | + | height=170 |
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/ordenenz_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | <center>[http://maralboran.org/web_ma/descartes/3_eso/Potencias_mac/potencias1_1.html '''Click''' aquí si no se ve bien la escena]</center> |
| }} | }} | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividad Interactiva: ''Potencias de números enteros''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado=2. Autoevaluación. | + | |enunciado='''Actividad 1.''' Potencias de base negativa. |
| |actividad= | |actividad= | ||
| - | En esta escena deberas decir que número es el mayor. Anota los resultados en tu cuaderno. | + | Calcula las siguientes potencias y comprueba los resultados en la escena siguiente: |
| - | Pulsa INICIO cada vez que quieras ver un ejemplo nuevo. | + | a) <math>(-3)^4</math>{{b}}b) <math>(-4)^5</math>{{b}}c) <math>(-10)^5</math>{{b}}d) <math>(-2)^{10}</math> |
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/ordenenz_2.html | + | url=http://maralboran.org/web_ma/descartes/3_eso/Potencias/potencias31_1.html |
| width=500 | width=500 | ||
| - | height=325 | + | height=230 |
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/ordenenz_2.html '''Click''' aquí si no se ve bien la escena]</center> | + | <center>[http://maralboran.org/web_ma/descartes/3_eso/Potencias/potencias31_1.html '''Click''' aquí si no se ve bien la escena]</center> |
| + | Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. | ||
| + | Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. | ||
| }} | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | ====Propiedades de las potencias==== | ||
| + | {{Caja Amarilla|texto=<center><math>a^0=1\,\!</math>{{b}}{{b}}<math>a^m \cdot a^n=a^{n+m}</math>{{b}}{{b}}<math>\cfrac{a^m}{a^n}=a^{m-n}\,\!</math>{{b}}{{b}}<math>(a^m)^n=a^{m \cdot n}</math> | ||
| + | </center> | ||
| + | {{p}} | ||
| + | <center><math>(a^n \cdot b^n)=(a \cdot b)^n</math>{{b}}{{b}}<math>\cfrac{a^n}{b^n}=\left ( \frac{a}{b} \right )^n\,\!</math> | ||
| + | </center> | ||
| }} | }} | ||
| + | [[Categoría: Matemáticas]][[Categoría: Números|Enteros]] | ||
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice Descartes Manual Casio | Definiciones Operaciones | WIRIS Calculadora |
Tabla de contenidos |
El conjunto de los números enteros
El conjunto de los números enteros es
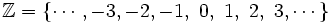
Representación de los números enteros
Podemos representarlos en una recta:
Orden en el conjunto de los enteros
En la representación de los enteros en la recta numérica se observa el orden que existe en el conjunto de los números enteros, siendo los números negativos menores que los positivos y que el cero.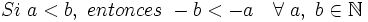
Operaciones con enteros
Las operaraciones con enteros son similares a las operaciones con naturales, pero con las peculiaridades que aportan los números negativos.
Opuesto de un entero
El opuesto de un número entero  es otro número entero
es otro número entero 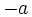 .
.
Suma y resta de enteros
La suma de números enteros es otro número entero. La resta de números enteros es otro número entero resultado de sumar el primero con el opuesto del segundo.
Jerarquía de las operaciones con enteros
Al operar con números enteros se atiende a la misma jerarquia de las operaciones con naturales.
Se efectúan primero el contenido de los paréntesis. De las operaciones, la de mayor prioridad es la potenciación, seguida de la multiplicación y las división y, para terminar, la suma y la resta. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
Multiplicación de enteros
Para multiplicar enteros usaremos la llamada regla de los signos: Si dos números enteros tienen el mismo signo su producto es un entero positivo. Y si tienen distinto signo, el producto es un entero negativo. Ésto es:
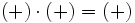 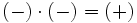 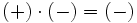 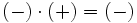 |
División de enteros
La división de números enteros, al igual que la división de números naturales, no siempre es otro entero. Con la división , al igual que con la multiplicación, se aplica la misma regla de los signos.
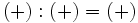 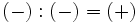 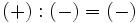 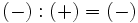 |
|
Actividad Interactiva: Operaciones combinadas
1. Operaciones combinadas y con paréntesis:
Actividad: En esta actividad debes marcar en la ventana bajo la escena el número que sigue al resolver la expresión. Cuando el número marcado sea el correcto aparecerá en la escena, si no es el correcto no aparecerá. Debes hacerlo sucesivamente, paso a paso, para ello debes borrar el número anterior. No se trata de que halles directamente el resultado final. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
|
Potencias de enteros
Las potencias de enteros cumplen las mismas propiedades que las potencias de números naturales.
Potencia de base negativa:
Al elevar un número negativo a una potencia, el resultado es positivo si el exponente es par y negativo si es impar.
|
Actividad Interactiva: Potencias de números enteros
Actividad 1. Potencias de base negativa.
Actividad: Calcula las siguientes potencias y comprueba los resultados en la escena siguiente: a) ( − 3)4 b) ( − 4)5 c) ( − 10)5 d) ( − 2)10 Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. |
Propiedades de las potencias