Teorema de Pitágoras. Aplicaciones
De Wikipedia
| Revisión de 19:00 26 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:06 26 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| ==Aplicaciones del teorema de Pitágoras== | ==Aplicaciones del teorema de Pitágoras== | ||
| ===Cálculo del lado desconocido en un triángulo rectángulo=== | ===Cálculo del lado desconocido en un triángulo rectángulo=== | ||
| - | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | + | {{Cálculo del lado desconocido en un triángulo rectángulo}} |
| - | A partir de la fórmula del teorema de Pitágoras: | + | |
| - | {{p}} | + | |
| - | <center><math>a^2+b^2=c^2\;\!</math></center> | + | |
| - | {{p}} | + | |
| - | podemos despejar cualquiera de los lados: | + | |
| - | {{p}} | + | |
| - | <center><math>c=\sqrt{a^2+b^2} \qquad a=\sqrt{c^2-b^2} \qquad b=\sqrt{c^2-a^2}</math></center> | + | |
| - | + | ||
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver como se resuelven algunos problemas típicos mediante el teorema de Pitágoras. | + | |
| - | |enlace=[https://www.geogebra.org/m/dW5Wj4Hd Problemas de aplicación del teorema de Pitágoras] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| ===Cálculo de la distancia entre dos puntos=== | ===Cálculo de la distancia entre dos puntos=== | ||
Revisión de 19:06 26 nov 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Teorema de Pitágoras
Teorema de Pitágoras
| En un triángulo rectángulo la hipotenusa al cuadrado es igual a la suma de los cuadrados de los catetos:
| 
|
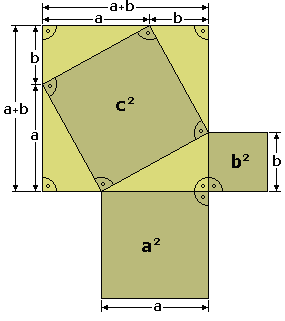
| Fíjate en la figura de la derecha y observa como el cuadrado grande, de lado a + b, puede descomponerse en un cuadrado de lado c y 4 triángulos rectángulos, como el de partida, de catetos a y b e hipotenusa c.
La superficie del cuadrado grande de lado a + b es: 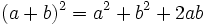 La superficie de los cuatro triángulos rectángulos es : 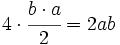 Restando el área del cuadrado grande de lado a + b menos las areas de los 4 triángulos rectángulos, se obtiene el área del cuadrado de lado c: 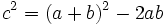 Desarrollando el cuadrado del binomio: 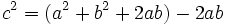 De donde obtenemos, simplificando: 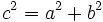 |
Teorema de Pitágoras:
Teorema de Pitágoras. Ejemplos y ejercicios.
Teorema de Pitágoras. Ejemplos y ejercicios.
Teorema de Pitágoras. Ejemplos.
Teorema de Pitágoras y recíproco. Ejemplo.
Demostraciones:
Demostración del teorema de Pitágoras mediante una construcción geométrica, con ejemplos previos de casos particulares.
La misma demostración del teorema de Pitágoras mediante una construcción geométrica, sin ejemplos previos.
Otra demostración basada en el teorema de la altura y el teorema del cateto.
Consta de tres partes:
Demostración del teorema de de la altura.
Demostración del teorema del cateto.
Demostración del teorema de Pitágoras.
Otros videos:
Pitágoras. El teorema de Pitágoras. Demostraciones.
Sin duda Pitágoras es el matemático más conocido del gran público. Todo el mundo recuerda su famoso teorema. Pero las Matemáticas le deben a Pitágoras y a los pitagóricos mucho más. Ellos son los que pusieron las primeras piedras científicas no solo de la Geometría sino también de la Aritmética, de la Astronomía y de la Música. Pero antes de Pitágoras otras dos culturas habían desarrollado unas matemáticas prácticas muy potentes: los babilonios y los egipcios. Exploraremos sus aportaciones tanto en el terreno de los sistemas de numeración que empleaban, como de sus habilidades astronómicas y geométricas. Del sistema sexagesimal de los babilonios hemos heredado tanto la división de la circunferencia en 360 grados como la forma actual de medir el tiempo en horas, minutos y segundos. Sus tablillas nos reservan unas cuantas sorpresas matemáticas. Quizás la más importante, la tablilla Plimpton, nos desvela el hecho sorprendente de que conocían las ternas pitagóricas mil años antes de que Pitagoras viera la luz.Disfrutaremos de alguna de las demostraciones gráficas más llamativas del famoso teorema, el que cuenta con un mayor número de demostraciones distintas a lo largo de la historia.
Esta unidad didáctica presenta varias demostraciones del teorema de Pitágoras.
En esta escena podrás comprobar el teorema de Pitágoras mediante el procedimiento gráfico de los cuadrados construidos sobre los lados del triángulo.
Aplicaciones del teorema de Pitágoras
Cálculo del lado desconocido en un triángulo rectángulo
Procedimiento
A partir de la fórmula del teorema de Pitágoras:
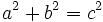
podemos despejar cualquiera de los lados:
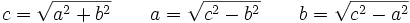
Enunciado y ejercicios del teorema de Pitágoras.
Tutorial en el que se explica y demuestra el teorema más famoso de las matemáticas, el TEOREMA DE PITÁGORAS, y se resuelven algunos ejercicios sencillos en los que se aplica dicho teorema.
- 00:00 a 03:00: Enunciado del Teorema de Pitágoras.
- 03:00 a 07:05: Demostración del Teorema de Pitágoras.
- 07:05 a 26:35: Ejercicios donde se aplica el Teorema de Pitágoras.
- 26:35 a 29:37: Teorema recíproco de Pitágoras.
Aprende a aplicar el teorema de Pitágoras.
Ejemplos de como se aplica el teorema de Pitágoras.
Ejercicios con el Teorema de Pitágoras.
Calcula la hipotenusa de un triángulo rectángulo cuyos catetos miden 6 y 8 cm, respectivamente.
Halla la distancia entre dos ciudades situadas en los vértices de un triángulo rectángulo.
Halla la distancia entre dos ciudades situadas en los vértices de un triángulo rectángulo.
Si la hipotenusa de un triángulo rectángulo mide 23 cm y uno de los catetos mide 6 cm, calcula el otro cateto.
Calcula la longitud de los lados desconocidos de dos triángulos rectángulos dados.
Calcula la longitud de los lados desconocidos de una figura dada.
Calcula la altura de un campo de cultivo con forma de triángulo isósceles, sabiendo que el perímetro es 450 y el lado desigual mide 160 m.
Calcula la diagonal de un rectángulo de base 4 cm ya altura 6 cm.
Un albañil está construyendo una pared rectangular de 12 m de base y 9 m de altura. En la diagonal quiere poner una cenefa para dividir la pared en dos partes iguales. ¿Cuántos metros de cenefa necesitará?. Si cada metro de cenefa cuesta 3.25 €, ¿tendrá suficiente con 50€?
Halla la diagonal de un cuadrado de 40 m de lado.
El triángulo equilátero: construcción y cálculo de la altura.
Cálculo de la diagonal de un cubo a partir de su arista.
Ejemplos y ejercicios de aplicación del teorema de Pitágoras.
En esta escena podrás ver como se resuelven algunos problemas típicos mediante el teorema de Pitágoras.
Actividades sobre el teorema de Pitágoras en Khan Academy.
Cálculo de la distancia entre dos puntos
Conocidas las coordenadas de dos puntos del plano, el teorema de Pitágoras nos permite calcular la distancia entre ambos:
En esta escena podrás ver como se calcula la distancia entre dos puntos del plano.
Clasificación de un triángulo atendiendo a sus ángulos conocidos sus lados
En un triángulo cualquiera, si llamamos a al lado mayor, y a los otros dos b y c, se cumple que:
- Si a2 > b2 + c2, el triángulo es obtusángulo
- Si a2 = b2 + c2, el triángulo es rectángulo
- Si a2 < b2 + c2, el triángulo es acutángulo
Clasificar un triángulo atendiendo a sus ángulos conocidos sus lados. Ejemplos.
Los lados de un triángulo miden 5, 2 y 3 cm, respectivamente. Averigua, sin dibujarlo, si es rectángulo.
Los lados de un triángulo miden 6, 8 y 11 cm, respectivamente. Averigua si es rectángulo.
Clasificación de los triángulos atendiendo a sus ángulos basada en la longitud de sus lados.
Ternas pitagóricas
- Se llaman ternas pitagóricas a las ternas de números naturales que verifican el teorema de Pitágoras.
- Las ternas cuyos tres números son primos entre sí, es decir, tales que m.c.d(a,b,c)=1, reciben el nombre de ternas pitagóricas primitivas.
- (3,4,5) es una terna pitagórica (52 = 32 + 42).
- También son ternas pitagóricas sus múltiplos: (6,8,10), (9,12,15), ... ,(3k,4k,5k) con
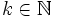 .
.
Las ternas pitagóricas. Ejemplos.
Generando ternas pitagóricas
Proposición
Si 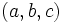 es una terna pitagórica entonces también lo es
es una terna pitagórica entonces también lo es 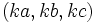 , con
, con 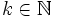 .
.
Sea (a,b,c) es una terna pitagórica. Se cumple:
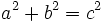 [1]
[1]Vamos a comprobar que (ka,kb,kc) también lo es y para ello veremos que también cumple el teorema de Pitágoras:
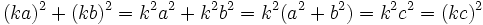
donde en el el penúltimo paso hemos utilizado la igualdad [1].
Por tanto, (ka,kb,kc) cumple el teorema de Pitágoras y es una terna pitagórica.En esta escena podrás ver como se generan ternas pitagóricas.
Proposición
Si 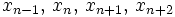 son cuatro términos cualesquiera de la sucesión de Fibonacci, entonces los siguientes números
son cuatro términos cualesquiera de la sucesión de Fibonacci, entonces los siguientes números
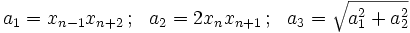
forman una terna pitagórica.
Se demuestra expresando los términos centrales de la subsucesión de Fibonacci, en función de los términos extremos y, luego, aplicando el teorema de Pitágoras para
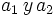 considerándolos como 'catetos'.
considerándolos como 'catetos'.


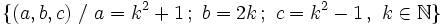 son ternas pitagóricas.
son ternas pitagóricas.
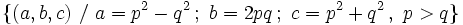 son ternas pitagóricas.
son ternas pitagóricas.

