Potencias y raíces de números enteros (2º ESO)
De Wikipedia
← Revisión anterior | Revisión siguiente →
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 36)
Potencias de números enteros
Bits, bytes, megas y más.
Los siguientes videotutoriales condensan lo que vamos a ver en este apartado sobre potencias de números enteros:
Cálculo de potencias cuya base es un número entero. Ejemplos.
Ejemplos de potencias de números enteros.
Tutorial en el que se explica a través de varios ejemplos la potencia con números enteros y las operaciones combinadas con multiplicación, división y potencia de números enteros.
- 00:00 a 05:55: Potencia de número enteros, definición.
- 05:55 a 09:15: Ejercicios simples de Potencias.
- 09:15 a 13:07: Ejercicios de Combinadas de Multiplicación, División y Potencias.
Potencias de números enteros.
Potencias de base entera y exponente natural. Producto de potencias. División de potencias. Potencias de una potencia. Potencia de un producto. Signo de una potencia.
Definición de potencia
La definición de potencia de exponente entero es la misma que la de números naturales.
Ver: Potencias de números naturales
Una potencia es un modo abreviado de escribir un producto de un número por sí mismo:
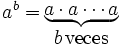 (Se lee: "
(Se lee: " elevado a
elevado a  ")
")- El número
 se llama base. Es el número que se multiplica por sí mismo.
se llama base. Es el número que se multiplica por sí mismo.
- El número
 se llama exponente. Es el número que indica las veces que la base aparece como factor.
se llama exponente. Es el número que indica las veces que la base aparece como factor.
- Por convenio, se establece que:
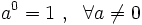 .
.
- Cuando el exponente de una potencia es el número 1 no se pone exponente, basta con poner el número de la base.
Cómo se leen las potencias:
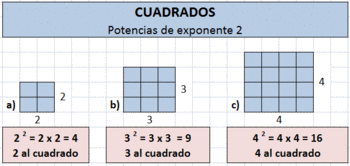
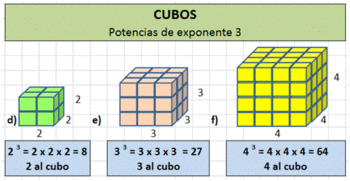
Cuando el exponente es 2 se dice "elevado al cuadrado", cuando el exponente es 3 se dice "elevado al cubo". En los demás casos se dice "elevado a la cuarta, quinta, sexta... potencia".
Actividad para aprender a calcular potencias de números enteros.
Actividades sobre potencias de números enteros.
Signo de la potencia
Signo de la potencia
Dependiendo del signo de la base tenemos dos posibilidades:
- Base positiva: Al elevar un número positivo a una potencia, el resultado es positivo.
- Base negativa: Al elevar un número negativo a una potencia, el resultado es positivo si el exponente es par y negativo si es impar.
Cálculo de potencias cuya base es un número entero negativo. Ejemplos.
1) Completa la tabla. En ella debes indicar la base, el exponente, el valor y la cómo se leen las siguientes potencias de números enteros:
2) Escribe en forma de potencia:
- a)
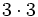
- b)
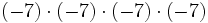
- c)
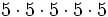
- d)
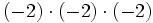
3) Escribe cómo se leen las siguientes potencias:
4) Escribe las siguientes potencias en forma de producto:
5) Escribe cada producto en forma de potencia, calcula su valor e indica cuál es la base y el exponente.
6) Calcula:
- a) Doce elevado al cuadrado.
- b) Once elevado al cubo.
- c) Tres elevado a la quinta.
- d) Dos elevado a la cuarta.
7) Desarrolla las siguientes potencias:
8) Calcula las siguientes potencias y razona cuánto valen todas las potencias de base 1:
- Actividad para aprender a calcular potencias de números enteros con base positiva o negativa.
- Actividad para practicar las potencias de enteros.
Calcula las siguientes potencias y comprueba los resultados en la escena siguiente:
a) ( − 3)4 b) ( − 4)5 c) ( − 10)5 d) ( − 2)10
Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Actividad sobre potencias cuya base es un número entero.
Ejercicios de autoevaluación en los que debes determinar el signo de la potencia cuya base es un número entero.
Ejercicios de autoevaluación de potencias cuya base es un número entero.
Ejercicios de autoevaluación de potencias cuya base es un número entero.
Ejercicios de autoevaluación de potencias cuya base es un número entero.
Propiedades de las potencias de enteros
Las potencias de números enteros cumplen las mismas propiedades que las potencias de números naturales.
Ver: Propiedades de las potencias de números naturales
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
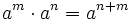
- 2. Cociente de potencias de la misma base:
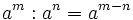
- 3. Potencia de un producto:
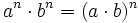
- 4. Potencia de un cociente:
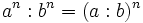
- 5. Potencia de otra potencia:
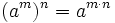
Propiedades de las potencias y ejemplos:
- Potencias de exponente 0.
- Potencias de exponente 1.
- Producto de potencias de la misma base.
- Cociente de potencias de la misma base.
Propiedades de las potencias y ejemplos:
- Potencia de otra potencia.
- Potencia de un producto.
- Potencia de un cociente.
Calcula:
- a)
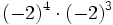 ; b)
; b) 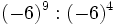
- c)
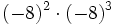 ; d)
; d) 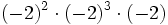
- e)
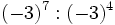 ; f)
; f) 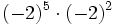
- g)
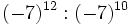 ; h)
; h) 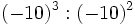
10) Escribe en forma de una sola potencia:
- a)
![[(-2)^3]^5\;](/wikipedia/images/math/8/8/6/886e30889b011f5f83334ec9296c0152.png) ; b)
; b) ![[(-3)^2]^3\;](/wikipedia/images/math/f/0/3/f037bb097909faad6873a0992df599fe.png)
- c)
![[(-5)^2]^4\;](/wikipedia/images/math/5/0/8/508d047dc4eb1a22b590a2f901a2fab9.png) ; d)
; d) ![[(-6)^3]^3\;](/wikipedia/images/math/4/c/8/4c8eef59c8fa17ac5bf2860de4ab42b4.png)
- e)
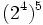 ; f)
; f) 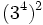
- g)
![[(-2)^1]^6\;](/wikipedia/images/math/d/f/3/df39089d6f5cc9c51e1d93713bb5f895.png) ; h)
; h) ![[(-2)^2]^6\;](/wikipedia/images/math/2/d/9/2d9edbe794a96dc0e0737db47be9067b.png)
- i)
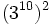 ; j)
; j) 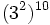
11) Expresa en forma de producto de varias potencias:
- a)
![[(-3) \cdot (-2) \cdot (-5)]^4\;](/wikipedia/images/math/3/2/6/3267df8521104f4db4a75cebb28001f7.png)
- b)
![[(-2) \cdot 5 \cdot (-6)]^2\;](/wikipedia/images/math/6/3/e/63e0b632e8c81875b6431d372a903f72.png)
- c)
![[2 \cdot 7 \cdot 6]^3\;](/wikipedia/images/math/1/a/0/1a083a19f18fa30e36b04f11289e2a1c.png)
- a)
![[(-2) \cdot (-3) \cdot (-6)]^3\;](/wikipedia/images/math/2/2/2/222cfc62f8027cac612dad7e3962dd04.png)
11) Expresa en forma de una sola potencia:
- a)
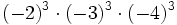
- b)
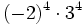
- c)
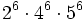
- d)
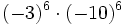
12) Calcula los cuadrados de los cinco primeros números positivos.
14) Escribe las cuartas potencias de: -3, -2, -5, 3, 2 y 5.
15) Calcula:
- a)
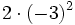 ; b)
; b) 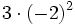
- c)
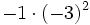 ; d)
; d) 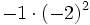
- e)
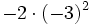 ; f)
; f) 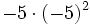
- g)
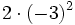
16) Escribe como potencias de base positiva:
17) Escribe el resultado como potencia de base positiva:
- a)
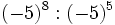 ; b)
; b) 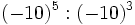
- c)
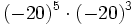 ; d)
; d) 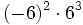
- e)
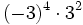 ; f)
; f) 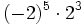
Simplifica: 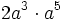
Simplifica: 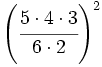
Simplifica: ![\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3](/wikipedia/images/math/7/1/b/71b5b62cb54ed835ba335fdbca4de909.png)
Simplifica: 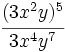
Simplifica: 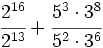
Actividades para aprender a calcular potencias de productos y cocientes.
Actividades para aprender a calcular productos y cocientes de potencias.
Actividades para aprender a calcular potencias de otra potencia.
Ejercicios resueltos sobre las propiedades de las potencias de números entero.
Actividades sobre las propiedades de las potencias de números enteros.
Ejercicios de autoevaluación sobre las propiedades de las potencias de números enteros.
Ejercicios de autoevaluación sobre las propiedades de las potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Ejercicios propuestos
|
Ejercicios propuestos: Potencias con números enteros |
|
Ejercicios propuestos: Propiedades de las potencias con números enteros |
Raíces cuadradas de números enteros
La definición de raíz cuadrada de un número entero es la misma que la dada para números naturales.
Ver: Raíz de un número natural
La raíz cuadrada de un número  es otro número
es otro número  que elevado al cuadrado da
que elevado al cuadrado da  . Simbólicamente:
. Simbólicamente:
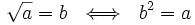
Al número  se le llama radicando y al número
se le llama radicando y al número  se le llama raíz.
se le llama raíz.
Número de soluciones de una raíz cuadrada
Dependiendo del signo del número entero, su raíz puede existir o no. Tenemos los dos casos siguientes:
Número de soluciones de la raíz cuadrada
- La raíz cuadrada de un número entero positivo tiene dos soluciones iguales pero opuestas en signo, que no siempre son números enteros.
- La raíz cuadrada de un número entero negativo no existe.
Raíz cuadrada de un número entero. Ejemplos
Simplificando raíces ccuadradas no exactas: 5\,\sqrt{117}
- Actividad para aprender a calcular raíces de números enteros.
- Actividad para practicar las raíces de números enteros.
Actividades sobre raíces cuadradas exactas y enteras.
Ejercicios de autoevaluación sobre raíces de números enteros.
Raíces cuadradas con la calculadora
|
Calculadora: Raíz cuadrada |
Ejercicios propuestos
|
Ejercicios propuestos: Raíces de números enteros |
Raíces cúbicas
La raíz cúbica de un número  es otro número
es otro número  que elevado al cubo da
que elevado al cubo da  . Simbólicamente:
. Simbólicamente:
![\sqrt[3]{a}=b \ \iff \ b^3=a](/wikipedia/images/math/8/2/f/82f2ca0f1bfe2e9b6bcbabcc5b7ba3ee.png)
Al número  se le llama radicando y al número
se le llama radicando y al número  se le llama raíz.
se le llama raíz.
Número de soluciones de una raíz cúbica
Con las raíces cuadradas, dependiendo del signo del número entero, su raíz puede existir o no. Con las raíces cúbicas siempre existe, pero es única.
Número de soluciones de la raíz cúbica
La raíz cúbica de un número entero tiene una única solución, que tiene el mismo signo que el radicando.
Raíz cúbica de un número entero. Ejemplos
Raíz cúbica de un número entero. Ejemplos
Simplificando raíces cúbicas no exactas: ![\sqrt[3]{3430}](/wikipedia/images/math/4/0/a/40acd601b8224df3d68ca6accc047204.png)
Calcula: ![\sqrt[3]{-512}](/wikipedia/images/math/d/5/0/d5007990ae7e9a5dddf6e4eff90d9a71.png)
Aprende a calcular raíces cúbicas.
Calcula raíces cúbicas.
Raíces de otros índices (Ampliación)
La raíz n-ésima 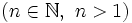 de un número
de un número  es otro número
es otro número  tal que
tal que 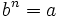 y que escribimos simbólicamente
y que escribimos simbólicamente ![b=\sqrt[n]{a}](/wikipedia/images/math/c/e/0/ce05f9d287d25fe0a5fd8e680bd177f5.png) .
.
![\sqrt[n]{a}=b \iff b^n =a](/wikipedia/images/math/f/f/7/ff79017c635440f207b67b250c3660fb.png)
El número  se llama radicando, el número
se llama radicando, el número  índice y
índice y  la raíz.
la raíz.
Si el índice es 2 las llamaremos raíces cuadradas; si el índice es 3, raíces cúbicas; si es 5, 6, ..., raíces cuartas, quintas, ....
Propiedades
Propiedades
![\sqrt[n]{1}=1](/wikipedia/images/math/f/2/3/f2301fcbef74b110ad8d373f2b32a16b.png) ;
; ![\sqrt[n]{0}=0](/wikipedia/images/math/8/6/5/865db751c6cb2e12533fccdf8de1e1df.png) , para cualquier valor del índice
, para cualquier valor del índice  .
.
- Si
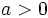 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) existe cualquiera que sea el índice
existe cualquiera que sea el índice  .
.
- Si
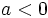 ,
, ![\sqrt[n]{a}](/wikipedia/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) sólo existe si el índice
sólo existe si el índice  es impar.
es impar.
- Si el índice
 es par y el radicando
es par y el radicando 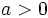 , la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto.
, la raíz tiene dos soluciones: una positiva y otra negativa, pero iguales en valor absoluto.
- Si el índice
 es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando
es impar, siempre tiene una única solución, que tiene el mismo signo que el radicando  .
.
Tutorial que explica la definición de raíz (radical) realizando el cálculo de alguna raíces exactas de números racionales (enteros y decimales).
Raíz n-ésmina de un número. Ejemplos sencillos.
Raíz n-ésmina de un número. Ejemplos más complejos.
Raíz n-ésmina de un número. Ejemplos sencillos.
- Raíces de un número entero.
- Raíces cuadradas y cúbicas.
- Partes de una raíz.
- Raíces de números positivo, negativos y del cero.
- Raíz exacta y raíz entera.
- Calculo manual de raíces cuadradas.
- Los radicales.
- Extracción de factores de un radical.
1) Completa:
- 1a)
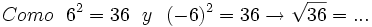
- 1b)
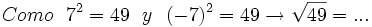
- 1c)
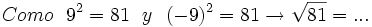
- 1d)
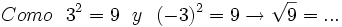
2) Completa:
- 2a)
![Como \ \ 6^3=216 \rightarrow \sqrt[3]{216}= ...](/wikipedia/images/math/3/c/3/3c378630d2615778e963ac624db86d87.png)
- 2b)
![Como \ \ (-6)^3=-216 \rightarrow \sqrt[3]{-216}= ...](/wikipedia/images/math/6/5/8/6587736293705d54e8f32954028d084c.png)
- 2c)
![Como \ \ 5^3=125 \rightarrow \sqrt[3]{125}= ...](/wikipedia/images/math/b/d/b/bdb68c764c3249b6a9780aa720742319.png)
- 2d)
![Como \ \ (-5)^3=-125 \rightarrow \sqrt[3]{-125}= ...](/wikipedia/images/math/e/7/0/e705216d0789f62aef7ec241081fabeb.png)
- 2e)
![Como \ \ 7^3=343 \rightarrow \sqrt[3]{343}= ...](/wikipedia/images/math/5/f/2/5f298eabe3ed377592f625e71f6488c0.png)
- 2f)
![Como \ \ (-7)^3=-343 \rightarrow \sqrt[3]{-343}= ...](/wikipedia/images/math/c/e/5/ce577674faca3babb2d3dfaac0413e21.png)
3) Completa:
- 3a)
![Como \ \ 6^4=216 \ \ y \ \ (-6)^4 =216 \rightarrow \sqrt[4]{216}= ...](/wikipedia/images/math/c/b/4/cb4b33e4c8e211ead755140a2c66bba9.png)
- 3b)
![Como \ \ 2^5=32 \ \ y \ \ (-2)^5 =32 \rightarrow \sqrt[5]{32}= ... \ \ y \ \ \sqrt[5]{-32}= ...](/wikipedia/images/math/c/c/c/ccc2a79c409e95a6ea8eb4d3dd464bae.png)
- 3c)
![Como \ \ 3^6=729 \ \ y \ \ (-3)^6 =729 \rightarrow \sqrt[6]{729}= ...](/wikipedia/images/math/b/5/5/b554d8cc9395627f020eb1f365124e4e.png)
- 3d)
![Como \ \ 2^7=128 \ \ y \ \ (-2)^7 =-128 \rightarrow \sqrt[7]{128}= ... \ \ y \ \ \sqrt[7]{-128}= ...](/wikipedia/images/math/a/d/6/ad64ef0e208078f3159cae14f80cd300.png)
- 3e)
![Como \ \ 3^8=6561 \ \ y \ \ (-3)^8 =6561 \rightarrow \sqrt[8]{6561}= ...](/wikipedia/images/math/7/b/a/7ba166f1a52a30e3ea2be20046fc6f29.png)
- 3f)
![Como \ \ 2^9=512 \ \ y \ \ (-2)^9 =-512 \rightarrow \sqrt[9]{512}= ... \ \ y \ \ \sqrt[9]{-512}= ...](/wikipedia/images/math/3/a/9/3a962574019bdc46ed38d924b83f207c.png)
- 3g)
![Como \ \ 2^{10}=1024 \ \ y \ \ (-2)^{10} =1024 \rightarrow \sqrt[10]{1024}= ...](/wikipedia/images/math/7/e/d/7edae10fccfe7b465c672d8c9c045b91.png)
4) Contesta:
- 4a) ¿Hay algún número que elevado al cuadrado dé -25? ¿Existe
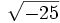 ?
?
- 4b) ¿Hay algún número que elevado al cuadrado dé -36? ¿Existe
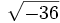 ?
?
- 4c) ¿hay algún número que elevado al cuadrado dé un número negativo?
- 4d) ¿Hay algún número que elevado al cubo dé -27? ¿Existe
![\sqrt[3]{-27}\;](/wikipedia/images/math/7/f/9/7f964050f55904a351871c909842d531.png) ?
?
- 4e) ¿Hay algún número que elevado al cubo dé -64? ¿Existe
![\sqrt[3]{-64}\;](/wikipedia/images/math/1/a/c/1ac847b9288b852f7e2cd46adb661650.png) ?
?
- 4f) ¿hay algún número que elevado al cubo dé un número negativo?
- 4g) ¿Hay algún número que elevado a la cuarta dé -81? ¿Existe
![\sqrt[4]{-81}\;](/wikipedia/images/math/9/3/8/9380cfbe25a5f6b1f53b0e98557d5cb3.png) ?
?
- 4h) ¿Hay algún número que elevado a la quinta dé -243? ¿Existe
![\sqrt[5]{-243}\;](/wikipedia/images/math/0/0/d/00d129c231e444389e6e90b5a1a8e808.png) ?
?
- 4i) ¿De qué depende que exista una raíz de radicando negativo?
5) Calcula:
- 5a)
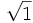 ;
; 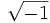
- 5b)
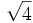 ;
; 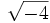
- 5c)
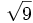 ;
; 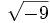
- 5d)
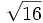 ;
; 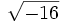
- 5e)
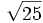 ;
; 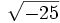
- 5f)
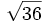 ;
; 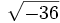
- 5g)
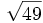 ;
; 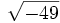
- 5h)
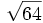 ;
; 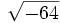
- 5i)
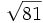 ;
; 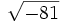
- 5j)
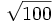 ;
; 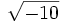
6) Calcula:
- 6a)
![\sqrt[3]{1}\;](/wikipedia/images/math/a/9/e/a9ed184fd0349444d061cc1d272e67c6.png) ;
; ![\sqrt[3]{-1}\;](/wikipedia/images/math/9/1/7/917ae3af6a2d50278779cc91cbbdea73.png)
- 6b)
![\sqrt[3]{8}\;](/wikipedia/images/math/1/3/2/132c2f74c8498afa99586eeab29a92a8.png) ;
; ![\sqrt[3]{-8}\;](/wikipedia/images/math/2/2/3/2232a48fe703bd572c3668d1f57c0066.png)
- 6c)
![\sqrt[3]{27}\;](/wikipedia/images/math/f/f/d/ffdb842d7cefcf30ac4e11b74ccdc8f3.png) ;
; ![\sqrt[3]{-27}\;](/wikipedia/images/math/7/f/9/7f964050f55904a351871c909842d531.png)
- 6d)
![\sqrt[3]{64}\;](/wikipedia/images/math/4/b/d/4bd0c615f84c6543e9f004c6bcfce737.png) ;
; ![\sqrt[3]{-64}\;](/wikipedia/images/math/1/a/c/1ac847b9288b852f7e2cd46adb661650.png)
- 6e)
![\sqrt[3]{125}\;](/wikipedia/images/math/9/b/0/9b0b656102d06b662a6c1cfa6f46ee4c.png) ;
; ![\sqrt[3]{-125}\;](/wikipedia/images/math/b/d/6/bd68acb8f905cf5984575d47adbbe028.png)
6) Calcula:
- 7a)
![\sqrt[4]{1}\;](/wikipedia/images/math/4/2/3/42348ffb6e4d069c36b7529b4c3d61c7.png) ;
; ![\sqrt[4]{-1}\;](/wikipedia/images/math/3/0/4/3041c7b2e1985e0ce2b4e12419b1adfd.png)
- 7b)
![\sqrt[5]{32}\;](/wikipedia/images/math/5/a/4/5a4316aef4d84ea09023226c0b455ef1.png) ;
; ![\sqrt[5]{-32}\;](/wikipedia/images/math/e/4/b/e4b2e7ef8b833cd852ca9c1bedfade9b.png)
- 7c)
![\sqrt[6]{729}\;](/wikipedia/images/math/6/4/5/645cad2d63e42973a6e2a66d954d5272.png) ;
; ![\sqrt[6]{-729}\;](/wikipedia/images/math/c/8/9/c89f55205c50d79be31feca9e8e7fe21.png)
- 7d)
![\sqrt[7]{128}\;](/wikipedia/images/math/e/4/e/e4e24abf54c49df327ec72213ca1b2bd.png) ;
; ![\sqrt[7]{-128}\;](/wikipedia/images/math/5/7/f/57ff532d80dc61569bbab4448a648df4.png)
8) Indica, en cada caso, la raíz, el índice y el radicando:
- 8a)
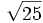
- 8b)
![\sqrt[3]{-64}\;](/wikipedia/images/math/1/a/c/1ac847b9288b852f7e2cd46adb661650.png)
- 8c)
![\sqrt[4]{81}\;](/wikipedia/images/math/0/4/d/04d103e445158aa43cb56526c68b98c2.png)
9) Completa:
- 9a)
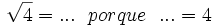
- 9b)
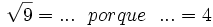
- 9c)
![\sqrt[3]{-8}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/b/b/c/bbc65bbad66511345d7cb3ac4f7a001c.png)
- 9d)
![\sqrt[3]{8}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/3/e/c/3ec4111d51daf4478bc80d3d1bd1ef0a.png)
- 9e)
![\sqrt[4]{16}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/2/0/8/208788fa3a4920a05007fa9edad8dbc6.png)
- 9f)
![\sqrt[5]{32}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/f/5/5/f552d101987249877deb51a2875a57db.png)
- 9g)
![\sqrt[5]{-32}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/a/b/9/ab988d19836d333dfc399b9f3fefee8c.png)
- 9f)
![\sqrt[6]{1}=... \ \ porque \ \ ... = 4\;](/wikipedia/images/math/7/0/6/70646a208681230895b71a7e18b7317b.png)
10) Calcula las raíces enteras por exceso y por defecto:
- 10a)
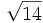 ;
; ![\sqrt[3]{14}\;](/wikipedia/images/math/4/d/9/4d90b08a8a7ba14e1c60f25be0fb24ef.png)
- 10b)
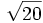 ;
; ![\sqrt[3]{20}\;](/wikipedia/images/math/f/a/a/faaf025a7b9f3b036eb836c60d8e4e34.png)
- 10c)
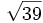 ;
; ![\sqrt[3]{39}\;](/wikipedia/images/math/c/9/f/c9f16a3fa799c3b21b4f313600db621c.png)
11) Calcula a mano las siguientes raíces:
- 11a)
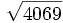
- 11b)

11) Calcula a mano las siguientes raíces:
- 11c)
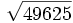
- 11d)
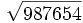
- 11e)
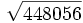
- 11f)
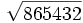
Actividades para que aprendas a calcular la raíz n-ésima de un número entero.
Operaciones combinadas con números enteros
A la hora de operar con números enteros utilizaremos la misma jerarquía de operaciones que con números naturales:
Ver: Jerarquía de las operaciones con números naturales
Jerarquía de las operaciones
A la hora de operar seguiremos las siguientes pautas:
- Primero se efectúan las operaciones del interior de los paréntesis. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
- Dentro de los paréntesis, o una vez quitados todos los paréntesis, las operaciones se efectúan en el siguiente orden:
- Las potencias y las raíces.
- Las multiplicaciones y las divisiones (de izquierda a derecha).
- Las sumas y las restas.
- Cuando aparecen paréntesis dentro de otros paréntesis, se puede optar por cambiar los paréntesis más exteriores por corchetes, con el fin de facilitar la lectura de la operación.
- Cuando resuelvas los paréntesis puedes completar las operaciones que encierren o aplicar la propiedad distributiva.
- En cada uno de los pasos que des para resolver una expresión con operaciones combinadas se puede llevar a cabo más de una operación, siempre que no suponga romper el orden que acabamos de establecer.
Tutorial en el que se explica a través de varios ejemplos el orden en el que hay que realizar las operaciones con números, lo que se llama la jerarquía de operaciones.
- 00:00 a 03:47 : Conceptos básicos. Jerarquía de operaciones.
- 03:47 a 19:37 : Ejercicios de Operaciones Combinadas.
Operaciones combinadas con enteros.
En esta escena podrás practicar las operaciones con números enteros: suma, resta, multiplicación, cociente, potencia y raíz; con o sin paréntesis.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros. Incluye raíces y potencias.
Problemas resueltos
1) En las carreras de caballos un espectador apostó en 4 carreras y los resultados fueron estos: en la primera perdió 50 €;, en la segunda perdió 30 €; en la tercera ganó 40 € y en la cuarta ganó 600 €. ¿Cuál fue el balance total de sus apuestas?
2) La temperatura de una ciudad medida a las 7 de la mañana es de 4º sobre cero; de 7 a 10, la temperatura aumentó 5º; de 10 a 2 la temperatura aumentó 4º; de 2 a 5 no varió; de 5 a 9 descendió 3º y de 9 a 12 descendió 7º. ¿Cuál es la temperatura a las 12 de la noche?
3) A primeros de mes, Luis tenía en su cuenta 500 €. Al día siguiente ingresó 50 €. Al otro día sacó 200 € y a la semana siguiente sacó 100 €. El día 29 ingresó 250 € que le pagó un amigo. ¿Qué dinero le queda a final de mes?
4) Una sustancia que se encuentra a 50º pasa a 5º bajo cero. ¿Cuál es la variación de la temperatura?
5) La temperatura de una barra de hielo en un día de invierno es de 2º bajo cero. Se calienta y pasa a 50º sobre cero. ¿Cuál es la variación de temperatura?
6) En un juego, Luis ganó 12 cromos, después perdió 15 cromos, más tarde ganó 27 cromos y luego perdió 7 cromos. ¿Cuál fue el balance del juego?
7) Una sustancia que está a 11º bajo cero se calienta hasta ponerse a 11º sobre cero. ¿Cuál es la variación de temperatura?
8) Al construir un edificio de 10 plantas y 3 sótanos, el nivel de la calle donde está se considera altura cero; por encima, las alturas son positivas, y por debajo, negativas. calcula la distancia recorrida por un ascensor que va:
- de la altura -7 a la altura +25.
- de la altura -2 a la altura -8.
- de la altura +4 a la altura +15.
1) Una colección de libros de historia consta de 150 libros. El precio de los tres primeros juntos es de 32 euros, y el precio de los restantes hasta la mitad de la colección se vende a 25 euros cada libro. La segunda mitad de la colección se vende a 22 euros cada libro. ¿Cuál es el importe total de la colección?
2) Una isla tiene una superficie de 140 km2, y la densidad de población en esta isla (número de habitantes por km2) es de 250. La isla tiene 6 árboles por persona. ¿Cuál es el número aproximado de árboles de la isla?
3) En una bodega hay las siguientes cantidades de vino:
- 8 toneles con 10 000 litros cada uno.
- 15 toneles con 8 hl cada uno.
- 20 toneles con 6 hl cada uno.
Calcula el total de litros de vino que hay en la bodega.
Problemas de sumas y restas de enteros con o sin paréntesis.
Problemas resueltos con números enteros.
Problemas resueltos con números enteros.
Problemas resueltos con potencias y raíces de números enteros.
En esta escena podrás resolver problemas de compras en los que intervienen sumas, restas y multiplicaciones de números enteros.
|
Problemas: Operaciones con enteros
1. Estamos en la planta 345 de un gran rascacielos del futuro y bajamos en ascensor a la planta -15. ¿Cuánto tiempo tardaremos si el ascensor tarda 1 segundo en bajar 5 pisos?
Solución: 1' 12"
2. Pitágoras, filósofo y matemático griego, nació el año 582 a.C. y murió el año 496 a.C. ¿A qué edad murio? ¿Cuántos años han pasado hasta el año 2007 d.C. desde su muerte?
Solución:
3. Durante el ascenso a una montaña, la temperatura desciende 2 grados cada 200 m de ascenso. ¿A qué altura habrá que ascender para alcanzar -15ºC, si en el punto de partida, la temperatura es de 5ºC y este está a una altitud de 300 m?
Solución: 2.300 m. |
Calculadora
Suma, resta, multiplicación y división
|
Calculadora: Suma, resta, multiplicación y división |
Opuesto
|
Calculadora: Opuesto |
Paréntesis
|
Calculadora: Paréntesis |
Potencias
|
Calculadora: Potencias |
Raíz cuadrada
|
Calculadora: Raíz cuadrada |
Raíz cúbica
|
Calculadora: Raíz cúbica |
Otras raíces
|
Calculadora: Otras raíces |

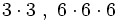
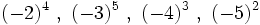
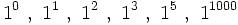
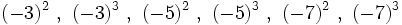
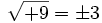
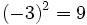
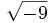 no existe, porque no hay níngún número cuyo cuadrado sea negativo, -9.
no existe, porque no hay níngún número cuyo cuadrado sea negativo, -9.
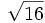
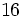
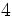
![\sqrt[3]{+8}= +2](/wikipedia/images/math/d/b/1/db1e76a0ee49262bcb030cc293755d1a.png)

![\sqrt[3]{-8}= -2](/wikipedia/images/math/1/5/4/154ab22db729e6b6490caa36d8669830.png)
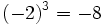
![\sqrt[5]{32}=2\;](/wikipedia/images/math/e/f/a/efae07f29bbbaaef03acb5b46afffb59.png) porque
porque 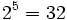 .
.
![\sqrt[3]{1}=1](/wikipedia/images/math/d/5/3/d53d30c7123945d21786c0fb38eeeb18.png) .
.
![\sqrt[5]{0}=0](/wikipedia/images/math/e/9/5/e95b8cee4e9e352608032036b0bd68d7.png) .
.
![\sqrt[4]{16}=\pm 2](/wikipedia/images/math/3/5/c/35cc75069a6350b569ad8c8f72bf6ae2.png) porque
porque 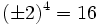 .
.
![\sqrt[3]{64}=4](/wikipedia/images/math/f/2/4/f2482a82a1ce97518a3bbef09d9575b5.png) porque
porque 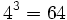 .
.
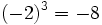 .
.
![\sqrt[4]{-8}= no \ existe](/wikipedia/images/math/a/2/1/a21d3d89fedd78f5c9a6378b3cf240f3.png) porque ningún número elevado a 4 puede dar negativo (-8).
porque ningún número elevado a 4 puede dar negativo (-8).
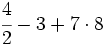


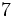
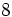
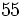
![\sqrt [3] {8}](/wikipedia/images/math/f/5/2/f5234f8dd97fefc954cf62fa258a3b72.png)
![\sqrt [4]{81}](/wikipedia/images/math/e/c/6/ec6e7957bf989cbaf4c80a2e4c59755c.png)