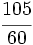Números racionales: Definición
De Wikipedia
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Fracciones I Fracciones II Fracciones III Fracciones IV | Fracciones | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Fracciones y números racionales
Los números enteros son útiles para contar u ordenar objetos, pero hay veces en las que es necesario dividir la unidad en partes iguales para poder expresar una medida: la mitad, la tercera parte, etc. Estas medidas se expresan por medio de fracciones.
- Una fracción es una expresión de la forma
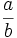 , o bien,
, o bien, 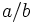 , donde
, donde  y
y  son números enteros, siendo
son números enteros, siendo 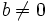 .
.
- Al número
 lo llamaremos numerador y al número
lo llamaremos numerador y al número  , denominador.
, denominador.
Una fracción se puede interpretar como una cantidad determinada de porciones que se toman de un todo dividido en partes iguales:
- El denominador sirve para representar las partes en que se divide la unidad.
- El numerador sirve para representar las porciones que tomamos.
El valor de una fracción es el resultado de dividir numerador entre denominador. Según su valor, una fracción pueden ser:
- Un número entero: Si el resultado de hacer la división es exacto.
- Un número fraccionario: Si el resultado de hacer la división no es exacto.
Esta definición nos da otra forma de interpretar a una fracción, ya que nos permite verla como una "división indicada" en las que el dividendo es el numerador y el cociente el denominador.
Tutorial que explica el concepto de fracción y su representación gráfica, en partes de la unidad y en la recta numérica.
- 00:00 a 04:14: Conceptos básicos. Ejemplos introductorios.
- 04:14 a 05:38: Definición matemática de fracción.
- 05:38 a 09:45: Representación de fracciones como partes de la unidad (Ejemplos).
- 09:45 a 19:26: Representación de fracciones en la recta numérica (Ejemplos).
- 11:25 a 13:45: Aplicación del Teorema de Tales para la división de segmentos en partes iguales.
- Definición de fracción.
- Fracciones equivalentes.
- Simplificación de fracciones. Fracciones irreducibles.
Clasificación de las fracciones:
- Fracciones propias e impropias.
- Fracciones ordinarias y decimales.
- Fracciones homogeneas y heterogeneas.
- Fracciones irreducibles y reducibles.
El conjunto de los números racionales es el conjunto de todas las fracciones: 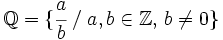 Obseva que:
Proposición La suma y el producto de dos números racionales es otro número racional. Demostración: Demostración de que la suma y el producto de dos racionales es racional. El conjunto de los números racionales El conjunto de los números racionales El conjunto de los números racionales. Introducción a números racionales e irracionales. |
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Fracciones propias e impropias
¿Qué pasa si el numerador es mayor que el denominador? ¿Cómo se interpreta el hecho de tomar más partes de la unidad de las que que hay?
Vamos a dar respuesta a estas preguntas a continuación, pero primero necesitamos ver los conceptos de fracción propia e impropia.
- Fracciones propias son aquellas cuyo numerador (en valor absoluto) es menor que el denominador (en valor absoluto). Su valor absoluto es menor que 1.
- Fracciones impropias son aquellas que no son propias. Su valor absoluto es mayor que 1.
Representación gráfica de fracciones propias e impropias.
Actividad en la que debes separar las fracciones propias de las impropias
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Las fracciones impropias representan algo mayor que el todo, es decir, cuando trabajamos con una fracción impropia damos a entender que tenemos unidades completas de algo y, posiblemente, alguna unidad incompleta.
Esto queda de manifiesto en la proposición y en los ejemplos que damos a continuación.
Proposición Toda fracción impropia, 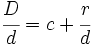
donde Demostración:
|
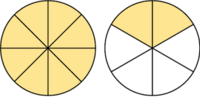
Ejemplo 1:
La fracción 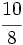 es impropia.
es impropia.
Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 4):
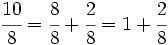
Ejemplo 2:
La frácción 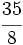 es impropia. La podemos decomponer en la suma de un entero y una fracción propia.
es impropia. La podemos decomponer en la suma de un entero y una fracción propia.
Para ello, dividimos 35 entre 8:
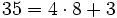
El dividendo 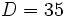 , el divisor
, el divisor 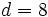 , el cociente
, el cociente 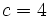 y el resto
y el resto 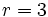 .
.
Aplicando la proposición anterior:
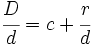
y sustituyendo cada letra por su valor:
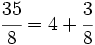
Actividades sobre el signo de las fracciones y sobre la descomposición de fracciones impropias como suma de un entero y una fracción propia.
Números mixtos
Una fracción mixta o número mixto es la representación de una fracción impropia como un número entero más una fracción propia, en la que se omite el signo de suma.
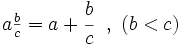
La fracción situada a la derecha del entero suele escribirse con una tipografía de menor tamaño para que no se confunda con una multiplicación de un número por una fracción.
Números mixtos. Ejemplos de paso de forma fraccionaria a mixta y viceversa.
Conversión de fracción impropia a número mixto
Conversión de fracción impropia a número mixto.
Conversión de fracción impropia a número mixto.
Escribiendo una fracción impropia com un número mixto
Convierte a número mixto la siguiente fracción impropia: 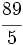
Nota: En el video, la división está realizada por el método anglosajón
Convierte a número mixto la siguiente fracción impropia: 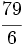
Nota: En el video, la división está realizada por el método anglosajón
Conversión de número mixto a fracción impropia
Conversión de número mixto a fracción impropia.
Conversión de número mixto a fracción impropia.
Convierte a fracción impropia el siguiente número mixto: 
Nota: En el video, la división está realizada por el método anglosajón
Convierte a fracción impropia el siguiente número mixto: 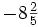
Nota: En el video, la división está realizada por el método anglosajón
Números mixtos y fracciones impropias.
Actividades de nivel variable en las que deberás obtener la forma mixta de una fracción.
|
Calculadora: Fracciones mixtas |
Representación de fracciones en la recta numérica
La representación de números enteros en la recta es algo muy sencillo. Como los enteros son "completos", la distancia entre dos consecutivos siempre es la misma, por lo que basta con escoger esa distancia para nuestra representación. Así, sí quisiésemos situar el número 7, por ejemplo, sólo tendríamos que contar siete saltos hacia la derecha desde el 0. Si quisiésemos representar un número negativo, los saltos serían hacia la izquierda del 0.
Sin embargo, para las fracciones no resulta tan sencillo, porque pueden representar cantidades que no son "completas" y hay que tener mucho cuidado con las distancias que se marcan.
Entonces, ¿cómo representamos una fracción en la recta? Para las fracciones propias es muy sencillo y para las impropias, basta con descomponerlas en parte entera más fracción propia.
Representación de fracciones en la recta numérica
- Si la fracción representa un número entero (el cociente entre numerador y denominador es exacto), la representaremos como tal. (Ver: Números enteros).
- Si la fracción es propia y positiva, se divide el segmento unidad de extremos 0 y 1, en tantas partes iguales como indique el denominador y contamos, desde el 0 hacia la derecha, tantas de esas partes iguales como indique el numerador.
- Si la fracción es propia y negativa, se divide el segmento unidad de extremos -1 y 0, en tantas partes iguales como indique el denominador y contamos, desde el 0 hacia la izquierda, tantas de esas partes iguales como indique el numerador.
- Si la fracción es impropia y positiva, se expresa en la forma
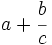 ("valor entero" + "fracción propia") y dividimos el segmento de extremos a y a+1 en c partes iguales y contamos, desde el punto a, hacia la derecha, b de esas partes iguales.
("valor entero" + "fracción propia") y dividimos el segmento de extremos a y a+1 en c partes iguales y contamos, desde el punto a, hacia la derecha, b de esas partes iguales.
- Si la fracción es impropia y negativa, se expresa en la forma
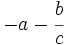 ("-valor entero positivo" - "fracción propia de números positivos") y dividimos el segmento de extremos -(a+1) y -a en c partes iguales y contamos, desde el punto -a, hacia la izquierda, b de esas partes iguales.
("-valor entero positivo" - "fracción propia de números positivos") y dividimos el segmento de extremos -(a+1) y -a en c partes iguales y contamos, desde el punto -a, hacia la izquierda, b de esas partes iguales.
Para dividir un segmento en parte iguales podemos utilizar el Teorema de Thales. Puedes verlo en el siguiente video:
En este vídeo aplicaremos el Teorema de Tales para dividir un segmento en partes iguales.
Ejemplo: Representación de fracciones en la recta numérica
Representa las fracciones:
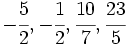
Nota: Pasa las fracciones impropias a forma mixta.
Tutorial que explica el concepto de fracción y su representación gráfica, en partes de la unidad y en la recta numérica.
- 00:00 a 04:14: Conceptos básicos. Ejemplos introductorios.
- 04:14 a 05:38: Definición matemática de fracción.
- 05:38 a 09:45: Representación de fracciones como partes de la unidad (Ejemplos).
- 09:45 a 19:26: Representación de fracciones en la recta numérica (Ejemplos).
- 11:25 a 13:45: Aplicación del Teorema de Tales para la división de segmentos en partes iguales.
Representación del conjunto de los racionales en la recta real.
Representación de fracciones en la recta numérica.
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Escribe la fracción que representa cada una de las letras representadas en la recta numérica.
Escribe la fracción que representa cada una de las letras representadas en la recta numérica.
Representa sobre la misma recta las fracciones 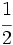 ,
, 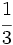 y
y 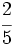 .
.
Representa sobre la misma recta las fracciones 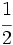 ,
, 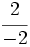 ,
, 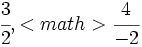 \;</math> y
\;</math> y 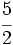 .
.
Representa sobre la misma recta las fracciones 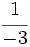 ,
, 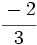 ,
, 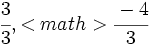 \;</math> y
\;</math> y 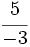 .
.
Representa en la recta real las fracciones 14/5 y -7/4.
Actividad en la que podrás ver como se representan gráficamente fracciones en la recta numérica.
Escribe la fracción impropia que corresponda a cada punto marcado en la recta.
En esta escena podrás comprobar si sabes representar fracciones en la recta numérica.
Haz en tu cuaderno la representación de las siguientes fracciones en la recta numérica:
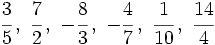
Compruéba las soluciones en la siguiente escena:
Fracciones equivalentes
| El siguiente videotutorial condensa todo lo que se va a ver en este tema sobre fracciones equivalentes:
Tutorial que explica el concepto de fracciones equivalentes y como obtener la fracción irreducible a una dada.
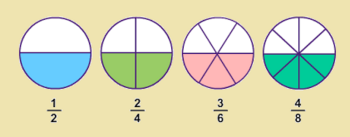
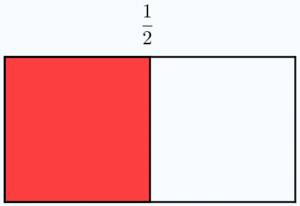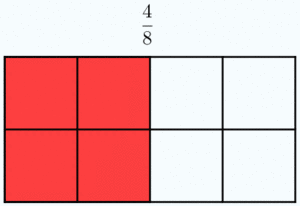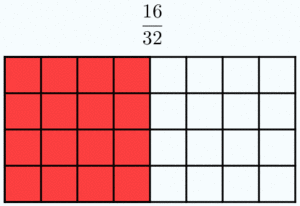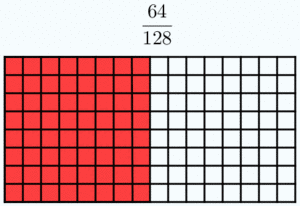
Dos fracciones son equivalentes si tienen el mismo valor. En la Fig.1 tienes ejemplos de fracciones equivalentes. Fíjate como representan la misma porción de la unidad aunque sus numeradores y denominadores sean diferentes.
Introducción a fracciones equivalentes. Modelos de fracciones equivalentes. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe las fracciones que representen cada uno de los puntos representados en la recta numérica. ¿Qué puedes decir de esas fracciones? Escribe las fracciones que representen cada uno de los puntos representados en la recta numérica. ¿Qué puedes decir de esas fracciones? Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Calcula cuatro fracciones equivalentes a Calcula cuatro fracciones que representen al número racional |
Obtención de fracciones equivalentes
| Piensa un número. Multiplícalo por 2. Divide el resultado entre 2. ¿Qué sucede?. Lógicamente, el número vuelve a ser el que era al principio porque la multiplicación y la división son operaciones inversas.
Esta idea, junto al hecho de que las fracciones sean el cociente de dos números enteros, permite que muchas fracciones representen el mismo número racional. Más que muchas, infinitas. Piensa, por ejemplo, en la fracción 1/2. Si multiplicamos su numerador y su denominador por el mismo número entero distinto de cero, en realidad, no estamos variando el valor de la fracción. Gráficamente, multiplicar el numerador y el denominador de una fracción por el mismo número significa partir el "todo" que estamos considerando en piezas más pequeñas, pero en realidad no varía la cantidad de ese "todo" que se toma. Fíjate en la animación para entenderlo mejor. |
Obtención de fracciones equivalentes
Si se multiplica o se divide (de forma exacta) el numerador y el denominador de una fracción por un mismo número distinto de cero, se obtiene una fracción equivalente. Si además el número por el que multiplicamos o dividimos es distinto de 1, estos procedimientos reciben el nombre de amplificación y simplificación, respectivamente.
En realidad, estos dos procesos son inversos el uno del otro. La única diferencia importante entre uno y otro es que, mientras la amplificación se puede hacer siempre, la simplificación sólo es posible si el numerador y el denominador tienen un divisor común mayor que 1.
Amplificación
| Simplificación
|
Obtención de fracciones equivalentes: por amplificación y por simplificación.
Obteniendo fracciones equivalentes por simplificación.
Obteniendo fracciones equivalentes por amplificación y simplificación.
Obtén dos fracciones equivalentes a 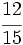 : una por amplificación y otra por simplificación.
: una por amplificación y otra por simplificación.
Escribe tres fracciones equivalentes a 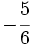 por amplificación.
por amplificación.
Escribe tres fracciones equivalentes a 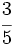 por amplificación.
por amplificación.
Escribe tres fracciones equivalentes a 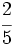 por amplificación.
por amplificación.
Escribe dos fracciones equivalentes a 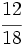 por amplificación.
por amplificación.
Halla una fracción equivalente a 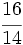 por amplificación y otra por simplificación.
por amplificación y otra por simplificación.
Escribe dos fracciones equivalentes a 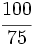 por simplificación.
por simplificación.
Escribe dos fracciones equivalentes a 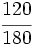 por simplificación.
por simplificación.
Escribe tres fracciones equivalentes a 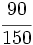 por simplificación.
por simplificación.
Busca una fracción equivalente a la dada con la ayuda del gráfico.
- a) Escribe una fracción equivalente a la dada.
- b) Empareja las fracciones equivalentes.
Fracciones equivalentes. Representación en la recta numérica.
Encontrar fracciones equivalentes por medio de la multiplicación.
Completa la fracción para que se cumpla la igualdad.
Completa la fracción para que se cumpla la igualdad.
Completa la fracción para que se cumpla la igualdad.
Encontrar fracciones equivalentes por medio de la multiplicación.
Simplificación de fracciones
- Simplificar una fracción es sustituirla por otra equivalente con el numerador y denominador menores que los de partida.
- Cuando una fracción no se puede simplificar se dice que es irreducible.
Procedimiento: Simplificación
- Para simplificar fracciones se divide numerador y denominador por un mismo número, distinto de 0 y 1. Este proceso se puede repetir hasta hacer la fracción irreducible.
- Si queremos hacer la fracción irreducible en un solo paso debemos dividir numerador y denominador por el m.c.d. de ambos.
Simplifica 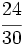 :
:
Solución:
- Paso a paso: Dividimos por 2 y luego por 3
- En un solo paso: Calculamos el m.c.d.(24,30) = 6, y dividimos directamente por 6:
Simplificación de fracciones (3 métodos). Fracción irreducible. Ejemplos.
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: | Simplifica: Simplifica: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: |
- Actividades en las que deberás simplificar fracciones con o sin ayuda.
- Actividad en la que debes emparejar cada fracción con su irreducible.
Actividad en las que deberás encontrar la fracción irreducible.
Actividades de nivel variable en las que deberás simplificar fracciones.
Simplifica fracciones.
La simplificación de fracciones me proporciona un método para saber si dos fracciones son equivalentes.
Procedimiento
Si al simplificar dos fracciones se obtiene la misma fracción irreducible, entonces las dos fracciones son equivalentes.
Determina si 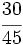 y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
son fracciones equivalentes.
Cómo averiguar si dos fracciones son equivalentes
Con lo que llevamos visto hasta ahora, tenemos dos formas de comprobar que dos fracciones son equivalentes:
- Calculando el valor de cada una de ellas, dividiendo numerador entre denominador, y viendo si el resultado es el mismo.
- Calculando la fracción irreducible de cada una de ellas y viendo si ambas fracciones irreducibles son iguales.
A continuación vamos a ver un resultado que permite hacer la comprobación de forma más simple. Lo llamaremos el método de multiplicar "en cruz".
Comprobación de que dos fracciones son equivalentes
Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden.
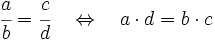
Cómo averiguar el término que falta en una igualdad entre fracciones
Si nos dan dos fracciones equivalentes y en una de ellas desconocemos uno de sus términos, utilizaremos el resultado anterior para averiguarlo.
Cálculo del término desconocido en una proporción. Ejemplos.
- Actividad 2a: Deberás escribir una fracción equivalente a la dada y verás la comprobación por el método de los productos cruzados.
- Actividad 2b: Actividad guiada en la que debes encontrar el término que falta de una igualdad entre fracciones.
Actividad en la que debrás averiguar el término que falta en una igualdad de fracciones.
Actividades
- Escribe, para cada apartado, las tres fracciones equivalentes que resultan de multiplicar el numerado y el denominador de la fracción dada por 2, 3 y 4, en ese orden.
- Encuentra la fracción irreducible para cada apartado.
- De la siguientes parejas de fracciones, señala aquellas que sean equivalentes.
- Completa para que las igualdades sean ciertas.
Ejercicios sobre fracciones equivalentes.
Ejercicios de autoevaluación sobre fracciones propias e impropias, fracciones equivalentes, fracciones irreducibles.
Recucir fracciones a común denominador
Comparar o sumar fracciones nos resultará mucho más fácil si éstas vienen dadas con el mismo denominador. Esto lo podemos conseguir gracias a la equivalencia de fracciones. Lo que tendríamos que hacer sería conseguir, a partir de las fracciones dadas, otras equivalentes pero que tengan el mismo denominador.
Reducir fracciones a común denominador consiste en sustituirlas por otras equivalentes con el mismo denominador.
Procedimiento: Reducir fracciones a común denominador
Para reducir fracciones a común denominador:
- Eligiremos como denominador a un múltiplo común de todos los denominadores. Normalmente se elige el m.c.m. de ellos.
- Amplificamos todas las fracciones para que tengan el mismo denominador, el que acabamos de calcular en el paso anterior. Para ello no tienes más que dividir ese denominador común entre el denominador inicial de la fracción correspondiente y multiplicar el resultado de esa división por el numerador inicial. El resultado de ese producto será el numerador de la fracción amplificada.
Ejemplo: Reducción de fracciones a común denominador
Reduce a común denominador las fracciones: 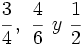
Calculamos el m.c.m. de los denominadores:
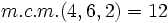 .
.
A continuación, multiplicaremos el numerador y denominador de cada fracción por el resultado de dividir ese m.c.m. por el denominador de cada fracción:
- Reducción de fracciones a comun denominador.
- Reduce a común denominador las siguientes fracciones:
a) 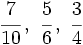
b) 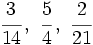
Reducción de fracciones a común denominador.
Reescribe las fraciones 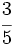 y
y 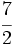 para que tengan denominador 10.
para que tengan denominador 10.
Considera las fraciones 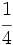 y
y 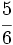 . Reescribe estas fracciones de manera que tengan el mismo denominador. ¿Qué números puedes usar para el denominador: 8, 12, 18, 24?
. Reescribe estas fracciones de manera que tengan el mismo denominador. ¿Qué números puedes usar para el denominador: 8, 12, 18, 24?
Reduce a común denominador 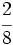 y
y 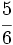 .
.
Reduce a común denominador 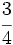 y
y 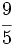 .
.
Reduce a común denominador 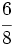 y
y 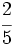 .
.
Reduce a común denominador 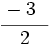 ,
, 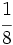 y
y 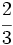 .
.
Reduce a común denominador 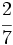 ,
, 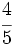 y
y 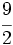 .
.
¿Son equivalentes 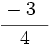 y
y 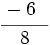 ? Redúcelas a común denominador. ¿Qué ocurre?
? Redúcelas a común denominador. ¿Qué ocurre?
Reduce a común denominador 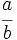 y
y 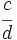 .
.
Actividad en la que verás como de ponen dos fracciones con el mismo denominador y su utilidad para sumar fracciones.
Reducción de fracciones a común denominador.
Reducción de fracciones a común denominador.
Ejercicios de autoevaluación sobre reducción de fracciones a común denominador.
Ejercicios de autoevaluación sobre reducción de fracciones a común denominador.
Orden en el conjunto de los racionales
Una forma de comparar fracciones consistía en calcular su valor numérico, efectuando la división. A continuación vamos a ver otras formas distintas de hacerlo. Distinguiremos los siguientes casos:
Caso 1: Las fracciones tienen numeradores o denominadores iguales
En algunos casos es fácil comparar dos fracciones sin necesidad de hacer la división. Esto será posible si ambas fracciones tienen los numeradores o denominadores iguales.
Comparar fracciones con numeradores o denominadores iguales
- De dos fracciones con el mismo denominador, es mayor la de mayor numerador.
- De dos fracciones con el mismo numerador, es mayor la de menor denominador.
Comparando fracciones con mismo denominador o mismo numerador.
Compara fracciones con el mismo numerador o denominador.
Caso 2: Las fracciones tienen numeradores y denominadores distintos
Veamos ahora un procedimiento para los casos en que no sean iguales ni los numeradores ni los denominadores. Lo que haremos será reducirlas a común denominador.
En la animación anterior, cuando los denominadores son distintos, no podemos comparar las piezas coloreadas de verde, pues son de tamaños distintos. Al cambiar los denominadores por 12, sí podemos hacer la comparación. Además, 12 no es un denominador cualquiera, es el mínimo común múltiplo de 3 y 4. Se podría usar cualquier otro múltiplo común, pero lo normal es usar el menor posible para no trabajar con números muy grandes.
Ordenar fracciones
- Para ordenar fracciones con distinto denominador debemos primero reducirlas a común denominador.
- Una vez reducidas a común denominador, será mayor la de mayor numerador.
Ejemplo: Ordenar fracciones
Ordena las siguientes fracciones: 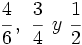
Calculamos el m.c.m. de los denominadores:
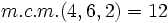 .
.
A continuación, las reducimos a común denominador:
Nótese que hemos multiplicado numerador y denominador por el resultado de dividir el m.c.m. , 12, por cada denominador.
Ordenamos las fracciones obtenidas, y a partir de ellas las fracciones de partida:
Ordena las siguientes fracciones:
a) 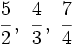
b) 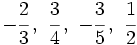
b) 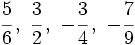
Comparación de fracciones. Ordenar fracciones de forma ascendente. Atención al método usado para obtener el m.c.m. Ordenar fracciones de forma descendente. Compara Compara Compara | Compara Compara Compara Compara las fracciones: Ordena las fracciones: Ordena las fracciones: |
Actividad en la que podrás ver como se comparan fracciones reduciéndolas a común denominador, tanto si son positivas como negativas.
Actividad en la que debes ordenas varias fracciones.
Actividad en la deberás comparar fracciones.
Ejercicios de autoevaluación sobre ordenación y comparación de fracciones.
Ordena fracciones.
Ejercicios
- Actividad en la que debes ordenas varias fracciones.
- Actividad en la que debes representar varias fracciones en la recta real.
|
Ejercicios: Fracciones equivalentes 1. Agrupa las fracciones que sean equivalentes: Solución: 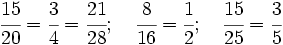 2. Simplifica las fracciones:
Solución: a) 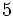 b) b) 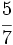 c) c) 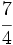 |
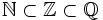
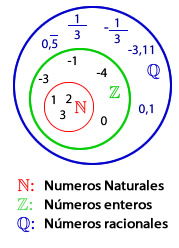
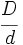 , se puede escribir como suma de un número entero y una fracción propia.
, se puede escribir como suma de un número entero y una fracción propia.
 es el cociente y
es el cociente y  es el resto de la división de
es el resto de la división de  entre
entre  .
.
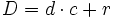
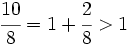
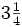 :
:
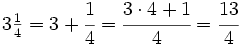
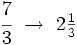 ; B)
; B) 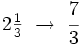
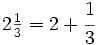
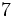

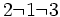 ; B)
; B) 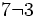
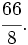
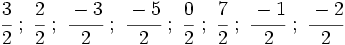
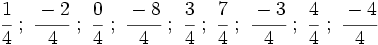
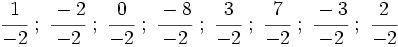
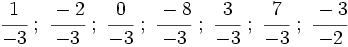
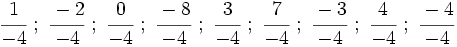
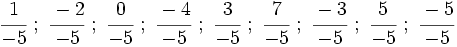
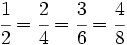
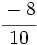 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
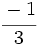 y
y 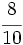 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
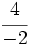 y
y 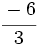 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
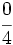 y
y 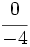 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
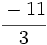 y
y 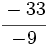 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
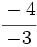 y
y 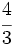 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
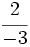 y represéntalas en la recta numérica.
y represéntalas en la recta numérica.
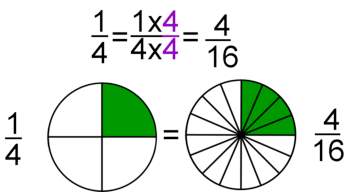
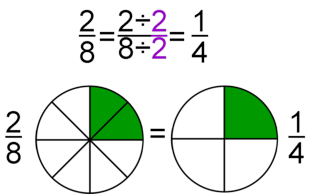
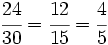
 b)
b) 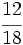
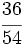 b)
b) 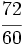
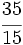 b)
b) 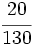
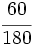 b)
b) 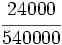
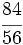 b)
b) 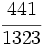
 b)
b) 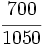
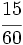
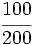 .
.
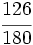 .
.
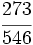 .
.
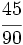 .
.
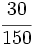 .
.
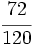 .
.
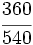 .
.
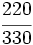 .
.
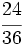 .
.
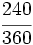 .
.
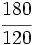 .
.
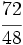 .
.
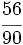 .
.
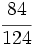 .
.
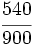 .
.
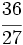 .
.
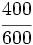 .
.
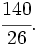
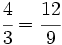 , porque
, porque 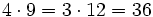 (son equivalentes)
(son equivalentes)
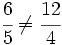 , porque
, porque 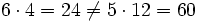 (no son equivalentes)
(no son equivalentes)
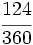 y
y 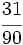 ?
?
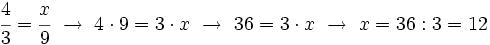
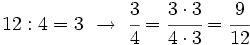
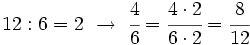
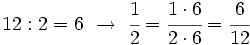
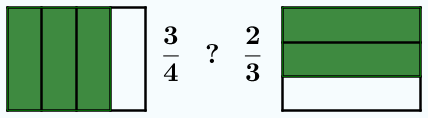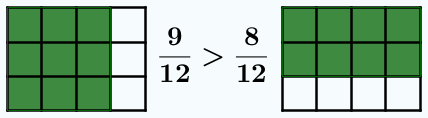
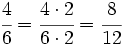
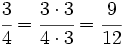
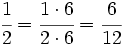
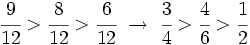
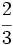 y
y 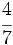 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
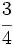 y
y 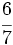 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
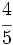 y
y 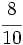 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
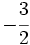 y
y 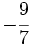 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
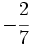 y
y 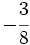 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
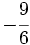 y
y 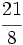 y
y 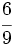 .
.
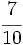 ,
, 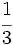 y
y 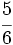 .
.
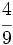 ,
, 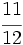 y
y 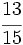 .
.
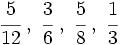
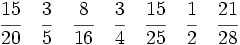
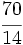 b)
b)  c)
c)