Números racionales
De Wikipedia
| Revisión de 15:08 21 oct 2017 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Los números racionales) |
||
| Línea 1: | Línea 1: | ||
| - | {{Menú Matemáticas 3ESO | + | {{Menú Matemáticas Contenidos Generales |
| |ir= |ampliar= | |ir= |ampliar= | ||
| |repasar= | |repasar= | ||
| - | [http://sultan.hostos.cuny.edu/InstructionalTech/MAT1604SPA/fractions.htm Fracciones I]<br>[http://descartes.cnice.mecd.es/1y2_eso/fracciones/index.htm Fracciones II]<br>[http://descartes.cnice.mecd.es/3_eso/Fracciones_decimales_porcentajes/index.htm Fracciones III]<br>[http://sultan.hostos.cuny.edu/InstructionalTech/MAT1604SPA/decimals.htm Números decimales]<br> | + | |enlaces= |
| - | |enlaces=[http://es.wikipedia.org/wiki/Fracci%C3%B3n Fracciones]<br> | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Números racionales== | + | =Fracciones= |
| - | Los números enteros son útiles para contar u ordenar objetos, pero hay veces en las que es necesario dividir la unidad en partes iguales para poder expresar una medida: la mitad, la tercera parte, etc. Estas medidas se expresan por medio de fracciones. | + | {{Introducción a las fracciones}} |
| {{p}} | {{p}} | ||
| - | {{def fraccion}} | + | ==Las fracciones== |
| + | {{Definición de fracción (1ºESO)}} | ||
| {{p}} | {{p}} | ||
| - | {{def cto racionales}} | + | ==Los números racionales== |
| + | {{el conjunto de los números racionales}} | ||
| + | {{p}} | ||
| + | {{Prohibido dividir por cero}} | ||
| {{p}} | {{p}} | ||
| {{wolfram desplegable|titulo=Números racionales|contenido= | {{wolfram desplegable|titulo=Números racionales|contenido= | ||
| Línea 17: | Línea 20: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ===Fracciones propias e impropias=== | + | |
| + | ==Fracciones propias e impropias== | ||
| {{Fracciones propias e impropias}} | {{Fracciones propias e impropias}} | ||
| {{p}} | {{p}} | ||
| Línea 27: | Línea 31: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ===Representación de fracciones en la recta numérica=== | + | ==Representación de fracciones en la recta numérica== |
| {{Representación de fracciones en la recta numérica}} | {{Representación de fracciones en la recta numérica}} | ||
| {{p}} | {{p}} | ||
| - | ==Fracciones equivalentes== | + | |
| - | El siguiente videotutorial condensa todo lo visto en este apartado sobre fracciones equivalentes: | + | =Fracciones equivalentes= |
| + | {{Fracciones equivalentes: definicion}} | ||
| {{p}} | {{p}} | ||
| - | {{Video: Fracciones equivalentes e irreducibles}} | + | ==Obtención de fracciones equivalentes== |
| + | {{Obtención de fracciones equivalentes}} | ||
| {{p}} | {{p}} | ||
| - | {{Fracciones equivalentes}} | + | ==Simplificación de fracciones== |
| + | {{Simplificación de fracciones}} | ||
| {{p}} | {{p}} | ||
| - | {{wolfram desplegable|titulo=Fracciones equivalentes|contenido= | + | ==Cómo averiguar si dos fracciones son equivalentes== |
| - | {{Wolfram fracciones equivalentes}} | + | {{Comprobación de que dos fracciones son equivalentes}} |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{Actividades fracciones equivalentes}} | + | ==Cómo averiguar el término que falta en una igualdad entre fracciones== |
| + | {{Cómo averiguar el término que falta en una igualdad entre fracciones}} | ||
| {{p}} | {{p}} | ||
| - | ===Simplificación de fracciones=== | + | ==Actividades== |
| - | {{Simplificación de fracciones}} | + | {{Actividades: Fracciones equivalentes}} |
| {{p}} | {{p}} | ||
| - | + | ==Recucir fracciones a común denominador== | |
| - | ===Recucir fracciones a común denominador=== | + | {{Reducción de fracciones a común denominador}} |
| - | {{Reducir fracciones a común denominador}} | + | |
| {{p}} | {{p}} | ||
| - | ==Ordenación de fracciones== | + | |
| + | =Ordenación de fracciones= | ||
| {{Ordenar fracciones}} | {{Ordenar fracciones}} | ||
| {{p}} | {{p}} | ||
| ==Actividades== | ==Actividades== | ||
| {{Actividades: Números racionales}} | {{Actividades: Números racionales}} | ||
| - | + | {{p}} | |
| - | + | =Operaciones con fracciones= | |
| - | + | ||
| - | --------- | + | |
| - | + | ||
| ==Suma y resta de fracciones== | ==Suma y resta de fracciones== | ||
| {{suma fracciones}} | {{suma fracciones}} | ||
| Línea 68: | Línea 72: | ||
| {{p}} | {{p}} | ||
| {{wolfram suma y resta fracciones}} | {{wolfram suma y resta fracciones}} | ||
| + | {{p}} | ||
| + | ===Opuesta de una fracción=== | ||
| + | {{Opuesta de una fracción}} | ||
| + | {{p}} | ||
| ==Multiplicación y división de fracciones== | ==Multiplicación y división de fracciones== | ||
| Línea 98: | Línea 106: | ||
| {{wolfram multiplicacion fracciones}} | {{wolfram multiplicacion fracciones}} | ||
| + | ===Inversa de una fracción=== | ||
| + | {{Inversa de una fracción}} | ||
| + | {{p}} | ||
| ===División de fracciones=== | ===División de fracciones=== | ||
| {{division fracciones}} | {{division fracciones}} | ||
| - | {{p}} | ||
| - | {{wolfram division fracciones}} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo division fracciones}} | {{Ejemplo division fracciones}} | ||
| {{p}} | {{p}} | ||
| {{actividades division fracciones}} | {{actividades division fracciones}} | ||
| + | {{p}} | ||
| + | {{wolfram division fracciones}} | ||
| + | |||
| + | ==Potencia de una fracción== | ||
| + | {{Def: potencia fracción}} | ||
| + | {{p}} | ||
| + | ===Potencias de exponente negativo=== | ||
| + | {{Def potencia exponente entero}} | ||
| + | {{p}} | ||
| + | {{AI potencias exponente entero}} | ||
| + | {{p}} | ||
| + | |||
| + | ===Propiedades de las potencias de números racionales=== | ||
| + | {{Propiedades de las potencias de números racionales}} | ||
| + | |||
| + | ==Raíces de fracciones== | ||
| + | {{Videos: raíces de fracciones}} | ||
| + | {{p}} | ||
| + | |||
| + | ==Racionalización== | ||
| + | Ver: [[Racionalización]] | ||
| + | {{p}} | ||
| ==Operaciones combinadas con fracciones== | ==Operaciones combinadas con fracciones== | ||
| {{Operaciones combinadas con fracciones 3ºESO}} | {{Operaciones combinadas con fracciones 3ºESO}} | ||
| {{p}} | {{p}} | ||
| - | |||
| ==La fracción como operador== | ==La fracción como operador== | ||
| Línea 143: | Línea 173: | ||
| <math>\cfrac{5}{24} \cdot 104\,000-\cfrac{1}{12} \cdot 104\,000=\left( \cfrac{5}{24}-\cfrac{1}{12} \right) \cdot 104\,000=\cfrac{1}{8} \cdot 104\,000= 13\,000</math> € | <math>\cfrac{5}{24} \cdot 104\,000-\cfrac{1}{12} \cdot 104\,000=\left( \cfrac{5}{24}-\cfrac{1}{12} \right) \cdot 104\,000=\cfrac{1}{8} \cdot 104\,000= 13\,000</math> € | ||
| - | |||
| - | |||
| - | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Video: La fracción como operador}} | {{Video: La fracción como operador}} | ||
| {{p}} | {{p}} | ||
| - | ===Ejercicios propuestos=== | ||
| - | {{ejercicio | ||
| - | |titulo=Ejercicios propuestos: ''La fracción como operador'' | ||
| - | |cuerpo= | ||
| - | (Pág. 15) | ||
| - | [[Imagen:red_star.png|12px]] 5, 6, 7 | ||
| - | |||
| - | |||
| - | }} | ||
| ==Ejercicios y problemas== | ==Ejercicios y problemas== | ||
| - | {{AI_cidead | + | {{Ejercicios y problemas con fracciones}} |
| - | |titulo1=Problemas con fracciones (Nivel 1) | + | |
| - | |descripcion=Problemas con fracciones. | + | |
| - | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena5/1quincena5_ejercicios_4d.htm | + | |
| - | }} | + | |
| - | {{AI_cidead | + | |
| - | |titulo1=Problemas con fracciones (Nivel 2) | + | |
| - | |descripcion=Problemas con fracciones. | + | |
| - | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena2/2quincena2_contenidos_4a.htm | + | |
| - | }} | + | |
| - | {{AI_cidead | + | |
| - | |titulo1=Problemas con fracciones (Nivel 3) | + | |
| - | |descripcion=Problemas para practicar operaciones con fracciones | + | |
| - | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena1/3quincena1_ejercicios_1b.htm | + | |
| - | }} | + | |
| - | {{Video: problemas fracciones}} | + | |
| - | {{Ejercicios_vitutor | + | |
| - | |descripcion=Problemas resueltos sobre fracciones. | + | |
| - | |url1=http://www.vitutor.com/di/r/problemas_fracciones_1.html | + | |
| - | |titulo1=Problemas resueltos: ''Fracciones'' | + | |
| - | }} | + | |
| - | {{Ejercicios_vitutor | + | |
| - | |descripcion=Ejercicios resueltos sobre fracciones. | + | |
| - | |url1=http://www.vitutor.com/di/r/b_a.html | + | |
| - | |titulo1=Ejercicios resueltos: ''Fracciones'' | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | ==Expresión decimal de una fracción== | + | =Expresión decimal de una fracción= |
| - | ===Paso de fracción a decimal=== | + | El siguiente videotutorial resume gran parte de lo que vamos a ver en este tema. |
| - | Para pasar de fracción a decimal basta con hacer la división del numerador entre el denominador. Pueden darse los siguientes casos, según sea la expresión decimal resultante:{{p}} | + | |
| - | {{Caja Amarilla|texto= | + | |
| - | *'''Expresión decimal exacta:''' Si tiene un número finito de decimales. | + | |
| - | :Por ejemplo: <math>\cfrac{7}{16}=0,4375</math>. | + | |
| - | *'''Expresión decimal periódica pura:''' Si tiene un número infinito de decimales que se repiten. La parte que se repite se llama '''periodo'''. | + | |
| - | :Por ejemplo: <math>\cfrac{6}{11}=0,545454...=0,\widehat{54}</math>. El periodo es 54. | + | |
| - | *'''Expresión decimal periódica mixta:''' Si tiene un número infinito de decimales que se repiten a partir de una cierta posición decimal. La parte que se repite se llama '''periodo''' y la parte decimal previa al periodo se llama '''anteperiodo'''. | + | |
| - | :Por ejemplo: <math>\cfrac{4}{15}=0,266666...=0,2\widehat{6}</math>. El periodo es 6 y el anteperiodo 2. | + | |
| - | }}{{p}} | + | |
| - | ===Identificar el tipo de expresión decimal sin hacer la división=== | + | |
| - | Se puede saber, sin hacer la división, que tipo de expresión decimal tiene una fracción. Para ello, deberemos simplificar la fracción y nos fijaremos en la descomposición del denominador en factores primos. Tendremos los siguientes casos: | + | |
| - | {{Caja_Amarilla|texto= | + | |
| - | * Si el denominador sólo contiene factores que sean 2 ó 5, la fracción tiene una expresión '''decimal exacta'''. | + | |
| - | * Si el denominador no contiene factores que sean 2 ó 5, la fracción tiene una expresión '''decimal periódica pura'''. | + | |
| - | * Si el denominador contiene mezcla de factores que sean 2 ó 5, con otros distintos de 2 ó 5, la fracción tiene una expresión '''decimal periódica mixta'''.}} | + | |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Expresión decimal de una fracción''|cuerpo= | + | {{Video_enlace_escuela |
| - | {{ai_cuerpo | + | |titulo1=Paso de decimal a fracción y viceversa |
| - | |enunciado='''Actividad 1.''' Averigua el tipo de expresión decimal de una fracción y hállala posteriormente | + | |duracion=11'04" |
| - | |actividad= | + | |sinopsis=En este video vamos a ver cómo se transforma una fracción en un número decimal y también cómo se calcula la fracción generatriz de los números decimales. |
| - | {{p}} | + | |
| - | Pulsa el botón "EJERCICIO" para generar una fracción. Debes averiguar de que tipo de expresión decimal se trata sin hacer la división. Luego halla su expresión decimal. | + | |
| - | + | ||
| - | Lo haces en tu cuaderno, escribe la solución en la casilla "Expresión Decimal" y pulsa el botón "SOLUCIÓN" para ver si lo has hecho bien. | + | |
| - | <center><iframe> | + | |url1=https://www.youtube.com/watch?v=4kGVaezCfXU |
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros2_2.html | + | |
| - | width=650 | + | |
| - | height=300 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | }} | + | |
| - | + | ||
| - | ===Paso de decimal a fracción=== | + | |
| - | Recíprocamente, todo número con un desarrollo decimal puede expresarse en fracción de la siguiente manera: | + | |
| - | {{Caja Amarilla|texto= | + | |
| - | '''Decimales exactos''': Se escribe en el numerador la expresión decimal sin la coma, y en el denominador un uno seguido de tantos ceros como cifras decimales. | + | |
| - | }}{{p}} | + | |
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_1.html | + | |
| - | width=540 | + | |
| - | height=210 | + | |
| - | name=myframe | + | |
| - | </iframe>{{p}} | + | |
| - | Pulsa INICIO para ver más ejemplos</center> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Caja Amarilla|texto= | + | |
| - | '''Decimales periódicos puros''': La fracción de un número decimal periódico tiene como numerador la diferencia entre el número escrito sin la coma y la parte anterior al periodo; y como denominador, tantos "9" como cifras tiene el periodo. | + | |
| - | }}{{p}} | + | |
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_2.html | + | |
| - | width=540 | + | |
| - | height=210 | + | |
| - | name=myframe | + | |
| - | </iframe>{{p}} | + | |
| - | Pulsa INICIO para ver más ejemplos | + | |
| - | </center> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Caja Amarilla|texto= | + | |
| - | '''Decimales periódicos mixtos''': Tendrá como numerador la diferencia entre ''a'' y ''b'', donde ''a'' es el número escrito sin la coma, y ''b'' es el número sin la parte decimal periódica, escrito como número entero. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras tenga el anteperiodo. | + | |
| - | }}{{p}} | + | |
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_3.html | + | |
| - | width=540 | + | |
| - | height=210 | + | |
| - | name=myframe | + | |
| - | </iframe>{{p}} | + | |
| - | Pulsa INICIO para ver más ejemplos | + | |
| - | </center> | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Veamos unos ejemplos que ilustren el porqué de tales procedimientos: | + | Para saber más sobre: [[Estructura de los números decimales (1º ESO)|Números decimales.]] |
| - | {{Ejemplo | + | ==Paso de fracción a decimal== |
| - | |titulo=Ejemplo: ''Paso de decimal a fracción'' | + | {{paso de fraccion a decimal}} |
| - | |enunciado= | + | |
| - | :Expresa en forma de fracción los números decimales: | + | |
| - | ::a) <math>15,\widehat{34}</math>{{b}} b) <math>12,3 \widehat{67}</math> | + | |
| - | |sol= | + | |
| - | :a) <math>\left . \begin{matrix} N=15,3434 \cdots \\100N=1534,3434 \cdots \end{matrix} \right \}</math> Restando: <math>100N-N=1534-15;\quad 99N=1519;\quad N=\cfrac{1519}{99}</math>{{p}} | + | |
| - | :b) <math>\left . \begin{matrix} N=12,36767 \cdots \\10N=123,6767 \cdots \\1000N=12367,6767 \cdots \end{matrix} \right \}</math> Restando: <math>1000N-10N=12367-123;\quad 990N=12244;\quad N=\cfrac{12244}{990}</math> | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{p}} | + | |
| - | {{AI2|titulo=Actividad Interactiva: ''Paso de decimal a fracción''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1.''' Averigua la fracción que corresponde con la expresión decimal. | + | |
| - | |actividad= | + | |
| {{p}} | {{p}} | ||
| - | Pulsa el botón "EJERCICIO" para generar una expresión decimal. Debes buscar la fracción generatriz. No olvides simplificarla. | ||
| - | Lo haces en tu cuaderno, escribes el numerador de la solución en el control numerador y el denominador de la solución en el control denominador y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien. | + | ==Paso de decimal a fracción== |
| + | {{Fracción generatriz}} | ||
| {{p}} | {{p}} | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros3_4.html | ||
| - | width=690 | ||
| - | height=300 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | }} | ||
| - | }} | ||
| - | ==Ejercicios y problemas== | + | =Ejercicios y problemas= |
| - | ===Ejercicios=== | + | |
| {{ejercicio | {{ejercicio | ||
| |titulo=Ejercicios: | |titulo=Ejercicios: | ||
| Línea 317: | Línea 220: | ||
| '''2. '''Simplifica las fracciones: | '''2. '''Simplifica las fracciones: | ||
| - | :a) <math>\cfrac{70}{14}</math>{{b}}b) <math>\cfrac{300}{420}</math>{{b}}c) <math>\cfrac{105}{60}</math> | + | :a) <math>\cfrac{70}{14}</math>{{b4}}{{b4}}b) <math>\cfrac{300}{420}</math>{{b4}}{{b4}}c) <math>\cfrac{105}{60}</math> |
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| - | a) <math>5\,\!</math>{{b}}b) <math>\cfrac{5}{7}</math>{{b}}c) <math>\cfrac{7}{4}</math> | + | a) <math>5\,\!</math>{{b4}}{{b4}}b) <math>\cfrac{5}{7}</math>{{b4}}{{b4}}c) <math>\cfrac{7}{4}</math> |
| }} | }} | ||
| Línea 339: | Línea 242: | ||
| '''4. '''Opera las fracciones: | '''4. '''Opera las fracciones: | ||
| - | :a) <math>\cfrac{7}{6} \cdot \cfrac{-2}{14} </math>{{b}}b) <math>\left ( \cfrac{3}{5}-\cfrac{2}{6} \right ):\cfrac{3}{15}</math>{{b}}c) <math>\cfrac{\cfrac {1}{3}-\left ( \cfrac{3}{4}-\cfrac{2}{6}+1 \right )}{2+\cfrac {2}{3}}</math> | + | :a) <math>\cfrac{7}{6} \cdot \cfrac{-2}{14} </math>{{b4}}{{b4}}b) <math>\left ( \cfrac{3}{5}-\cfrac{2}{6} \right ):\cfrac{3}{15}</math>{{b4}}{{b4}}c) <math>\cfrac{\cfrac {1}{3}-\left ( \cfrac{3}{4}-\cfrac{2}{6}+1 \right )}{2+\cfrac {2}{3}}</math> |
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| - | a) <math>-\cfrac{1}{6}</math>{{b}}b) <math>\cfrac{4}{3}</math>{{b}}c) <math>-\cfrac{13}{32}</math> | + | a) <math>-\cfrac{1}{6}</math>{{b4}}{{b4}}b) <math>\cfrac{4}{3}</math>{{b4}}{{b4}}c) <math>-\cfrac{13}{32}</math> |
| }} | }} | ||
| Línea 349: | Línea 252: | ||
| '''5. '''Simplifica y expresa en forma de fracción: | '''5. '''Simplifica y expresa en forma de fracción: | ||
| - | :a) <math>\cfrac{-5^2}{5^5}</math>{{b}}b) <math>\cfrac{0,001}{10^2} </math>{{b}}c) <math>\cfrac{(a^3 \cdot b^{-2})^2}{a^4 \cdot b^{-3}}</math> | + | :a) <math>\cfrac{-5^2}{5^5}</math>{{b4}}{{b4}}b) <math>\cfrac{0,001}{10^2} </math>{{b4}}{{b4}}c) <math>\cfrac{(a^3 \cdot b^{-2})^2}{a^4 \cdot b^{-3}}</math> |
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| - | a) <math>-\cfrac{1}{125}</math>{{b}}b) <math>\cfrac {1}{100.000}</math>{{b}}c) <math>\cfrac{a^2}{b}</math> | + | a) <math>-\cfrac{1}{125}</math>{{b4}}{{b4}}b) <math>\cfrac {1}{100.000}</math>{{b4}}{{b4}}c) <math>\cfrac{a^2}{b}</math> |
| }} | }} | ||
| Línea 359: | Línea 262: | ||
| '''6. '''Simplifica: | '''6. '''Simplifica: | ||
| - | :a) <math>\left ( \cfrac{-1}{5} \right )^3</math>{{b}}b) <math>\left [ \left ( \cfrac{-1}{3} \right )^{-2} \right ]^2</math>{{b}}c) <math>\left ( \cfrac{-1}{3} \right )^3 \cdot \left ( \cfrac{1}{-3} \right )^{-2}</math> | + | :a) <math>\left ( \cfrac{-1}{5} \right )^3</math>{{b4}}{{b4}}b) <math>\left [ \left ( \cfrac{-1}{3} \right )^{-2} \right ]^2</math>{{b4}}{{b4}}c) <math>\left ( \cfrac{-1}{3} \right )^3 \cdot \left ( \cfrac{1}{-3} \right )^{-2}</math> |
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| - | a) <math>-\cfrac{1}{125}</math>{{b}}b) <math>81 \;\!</math>{{b}}c) <math>-\cfrac{1}{3}</math> | + | a) <math>-\cfrac{1}{125}</math>{{b4}}{{b4}}b) <math>81 \;\!</math>{{b4}}{{b4}}c) <math>-\cfrac{1}{3}</math> |
| }} | }} | ||
| Línea 390: | Línea 293: | ||
| '''8. '''Sin hacer la división, indica qué tipo de decimal resulta: | '''8. '''Sin hacer la división, indica qué tipo de decimal resulta: | ||
| - | :a) <math>\cfrac{72}{15}</math>{{b}}b) <math>\cfrac{72}{9}</math>{{b}}c)<math>\cfrac{72}{35}</math> | + | :a) <math>\cfrac{72}{15}</math>{{b4}}{{b4}}b) <math>\cfrac{72}{9}</math>{{b4}}{{b4}}c)<math>\cfrac{72}{35}</math> |
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| - | a) Decimal exacto;{{b}}b) Decimal periódico puro;{{b}}c) Decimal periódico mixto. | + | a) Decimal exacto;{{b4}}{{b4}}b) Decimal periódico puro;{{b4}}{{b4}}c) Decimal periódico mixto. |
| }} | }} | ||
| Línea 400: | Línea 303: | ||
| '''8. '''Expresa en forma de fracción: | '''8. '''Expresa en forma de fracción: | ||
| - | :a) <math>21'379\;\!</math>{{b}}b) <math>2'\widehat{23}</math>{{b}}c) <math>21'45 \widehat{3}</math> | + | :a) <math>21.379\;\!</math>{{b4}}{{b4}}b) <math>2.\widehat{23}</math>{{b4}}{{b4}}c) <math>21.45 \widehat{3}</math> |
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| - | a) <math>\cfrac{21379}{1000}</math>{{b}}b) <math>\cfrac{221}{99}</math>{{b}}c) <math>\cfrac{19308}{900}</math> | + | a) <math>\cfrac{21379}{1000}</math>{{b4}}{{b4}}b) <math>\cfrac{221}{99}</math>{{b4}}{{b4}}c) <math>\cfrac{19308}{900}</math> |
| }} | }} | ||
| Línea 409: | Línea 312: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas:''Potencias'' | ||
| - | |cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Producto de potencias. | ||
| - | |actividad=Escribe en tu cuaderno los siguientes productos en forma de potencia: | ||
| - | <math>a)\ 2^3.2^7 \quad b)\ 3^5.3^3 \quad c)\ 5^5.5^3 \quad d)\ 2^{-3}.2^5 \quad e)\ 3^{-5}.3^{-3} \quad f)\ 5^{-5}.5^3 | ||
| - | </math> | ||
| - | <br> | ||
| - | Comprueba tus resultados en la siguiente escena. | ||
| - | <br> | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/wiki3eso/numeros/potencias/escenaspotencias/producto.html | ||
| - | width=100% | ||
| - | height=250 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 2:''' Cociente de potencias. | ||
| - | |actividad=Escribe en tu cuaderno los siguientes cocientes en forma de potencia: | ||
| - | <math>a)\ \frac{2^7}{2^3} \quad b)\ \frac{3^5}{3^3} \quad c)\ \frac{5^3}{5^3} \quad d)\ \frac{2^7}{2^{-3}} \quad e)\ \frac{3^{-2}}{3^2} \quad f)\ \frac{5^{-4}}{5^{-3}} | ||
| - | </math> | ||
| - | <br> | ||
| - | Comprueba tus resultados en la siguiente escena. | ||
| - | <br> | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/wiki3eso/numeros/potencias/escenaspotencias/cociente.html | ||
| - | width=100% | ||
| - | height=350 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 3:''' Potencia de un producto. | ||
| - | |actividad=Expresa en forma de producto de potencias los siguientes expresiones: | ||
| - | <math>a)\ (2.5)^6 \quad b)\ (3.4)^2 \quad c)\ (2.8)^3 \quad d)\ (4.6)^4 \quad e)\ (2.5)^{-2} \quad f)\ (3.2)^{-3} \quad g)\ (2.5)^{-3} | ||
| - | </math> | + | [[Categoría: Matemáticas]][[Categoría: Números|Racionales]] |
| - | <br> | + | |
| - | Calcula la solución en tu cuaderno y compruébalo en la escena siguiente. | + | |
| - | <br> | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/wiki3eso/numeros/potencias/escenaspotencias/potenciaproducto.html | + | |
| - | width=100% | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 4:''' Potencia de un cociente. | + | |
| - | |actividad=Expresa en forma de cociente de potencias los siguientes expresiones: | + | |
| - | <math>a)\ \left( \frac{8}{2} \right )^6 \quad b)\ \left( \frac{8}{4} \right )^2 \quad c)\ \left( \frac{10}{5} \right )^3 \quad d)\ \left( \frac{8}{4} \right )^{-2} \quad e)\ \left( \frac{10}{5} \right )^{-3} \quad f)\ \left( \frac{9}{3} \right )^{-4} | + | |
| - | </math> | + | |
| - | <br> | + | |
| - | Calcula la solución en tu cuaderno y compruébalo en la escena siguiente. | + | |
| - | <br> | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/wiki3eso/numeros/potencias/escenaspotencias/potenciacociente.html | + | |
| - | width=100% | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 5:''' Potencia de una potencia. | + | |
| - | |actividad=Escribe en tu cuaderno las siguientes potencias en forma de potencia con un solo exponente: | + | |
| - | <math>a)\ (2^3)^7 \quad b)\ (3^5)^3 \quad c)\ (5^5)^3 \quad d)\ (2^{-3})^2 \quad e)\ (3^3)^{-2} \quad f)\ (5^{-2})^{-3} | + | |
| - | + | ||
| - | </math> | + | |
| - | <br> | + | |
| - | Calcula la solución en tu cuaderno y compruébalo en la escena siguiente. | + | |
| - | <br> | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/wiki3eso/numeros/potencias/escenaspotencias/potenciapotencia.html | + | |
| - | width=100% | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | }} | + | |
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | WIRIS Geogebra Calculadora |
Tabla de contenidos
|
Fracciones
| Los números enteros surgen porque no bastaba con los números naturales para cubrir ciertas necesidades. Sin embargo, tampoco los enteros son suficientes. Hay muchas situaciones en las que necesitamos representar unidades incompletas. Por ejemplo, cuando vas al supermercado y compras un cuarto de kilo de gambas, es porque tienes suficiente con solo una parte y no necesitas la totalidad del kilo; o cuando te dicen que el 99% de una medusa es agua, te queda muy claro que le falta muy poco para ser toda agua, pero que no lo es en su totalidad.
Para estos casos se inventaron las fracciones. Curiosamente, desde un punto de vista histórico, las necesidad de las fracciones fue cubierta antes que la necesidad de los números negativos. Probablemente sea más natural hablar de partes incompletas de algo (fracciones) que de partes que "no están" (negativos). Fueron los egipcios, hace más de 3500 años, los primeros en usar fracciones. No utilizaban la barra que usamos nosotros para separar numerador de denominador, sino un símbolo parecido a un ojo, y sólo usaban el 1 como numerador (fracciones unitarias), pero sentaron las bases de lo que hacemos nosotros hoy en día. |
Un toque divertido para empezar el tema:
Si no fuera por las fracciones ni Troncho ni Poncho ni nadie podría celebrar su cumpleaños.
Puedes encontrar ejercicios sobre este vídeo y material similar en: http://www.angelitoons.com/
Actividades en las que se resume lo que se va a ver en este tema.
Las fracciones
Cuando necesitamos expresar cantidades que representan unidades incompletas o partes de la unidad, además de los números decimales, disponemos de las fracciones.
- Una fracción es una expresión de la forma
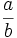 , o bien,
, o bien, 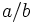 , donde
, donde  y
y  son números enteros, siendo
son números enteros, siendo 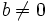 .
.
- Al número
 lo llamaremos numerador y al número
lo llamaremos numerador y al número  , denominador.
, denominador.
Una fracción se puede interpretar como una cantidad determinada de porciones que se toman de un todo dividido en partes iguales:
- El denominador sirve para representar las partes en que se divide la unidad.
- El numerador sirve para representar las porciones que tomamos.
El valor de una fracción es el resultado de dividir numerador entre denominador. Según su valor, una fracción pueden ser:
- Un número entero: Si el resultado de hacer la división es exacto.
- Un número fraccionario: Si el resultado de hacer la división no es exacto.
Esta definición nos da otra forma de interpretar a una fracción, ya que nos permite verla como una "división indicada" en las que el dividendo es el numerador y el cociente el denominador.
En la Fig. 2 tienes algunos ejemlos de fracciones representadas mendiante los llamados diagramas de tarta.
El valor de cada fracción se obtiene dividiendo el numerador entre el denominador:
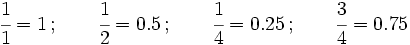
Fíjate que la unidad se puede representar mediante una fracción que tenga el mismo numerador que denominador.
En la Fig. 3 está representada la fracción 2/5. Fíjate como al hacer la división 2:5=0.4, se obtienen 4 décimas, que ocupan la misma porción que la fracción 2/5. Es decir, una fracción equivale a una división indicada.
Concepto de fracción. Términos. ¿Cómo se leen?
Representación gráfica de fracciones y de su expresión decimal.
Concepto de fracción. Fracciones propias e impropias.
Concepto de fracción. Fracciones propias e impropias.
Tutorial que explica el concepto de fracción y su representación gráfica, en partes de la unidad y en la recta numérica.
- 00:00 a 04:14: Conceptos básicos. Ejemplos introductorios.
- 04:14 a 05:38: Definición matemática de fracción.
- 05:38 a 09:45: Representación de fracciones como partes de la unidad (Ejemplos).
- 09:45 a 19:26: Representación de fracciones en la recta numérica (Ejemplos).
- 11:25 a 13:45: Aplicación del Teorema de Tales para la división de segmentos en partes iguales.
Fracciones unitarias (con numerador 1).
Importancia de dividir bien en partes iguales a la hora de representar fracciones gráficamente.
Tomando más de una parte del total.
Fracciones más grandes que la unidad.
Numerador y denominador de una fracción.
Fracciones en la recta numérica.
El plato de la cena de Vera está dividido en 3 secciones iguales. Si Vera puso brócoli en una sección del plato. ¿Qué fracci´´on del plato tiene brócoli?
Representa el punto 3/4 en la recta numérica.
Actividades sobre el significado de las fracciones.
Actividades sobre el significado de las fracciones.
- Actividad en la que se muestra y practica el concepto de fracción.
- Actividad en la que se explica y practica la representación gráfica de fracciones.
Actividades en las que se explica y practica cómo se lee una fracción.
Haz en tu cuaderno la representación de las siguientes fracciones en la recta numérica:
a) 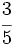 b)
b) 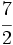 c)
c)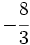 d)
d) 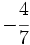 e)
e) 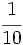 f)
f) 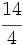
Compruéba las soluciones en la siguiente escena:
Corta figuras en partes iguales.
Reconoce fracciones.
Identifica numeradores y denominadores.
Las fracciones en la recta numérica
Fracciones unitarias en la recta numérica
Los números racionales
El conjunto de los números racionales es el conjunto de todas las fracciones: 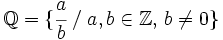 Obseva que:
Proposición La suma y el producto de dos números racionales es otro número racional. Demostración: Demostración de que la suma y el producto de dos racionales es racional. El conjunto de los números racionales El conjunto de los números racionales El conjunto de los números racionales. Introducción a números racionales e irracionales. |
Todo cociente de números cuyo denominador sea 0 carece de sentido matemático. De otro modo: si se admite la división por "cero" es el caos, pues entonces 2 = 1. Por eso,si divides por cero, aunque sea sin darte cuenta, serás fusilado de inmediato y expulsado de la comunidad científica por los siglos de los siglos.
¿Dónde está el error?
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Fracciones propias e impropias
¿Qué pasa si el numerador es mayor que el denominador? ¿Cómo se interpreta el hecho de tomar más partes de la unidad de las que que hay?
Vamos a dar respuesta a estas preguntas a continuación, pero primero necesitamos ver los conceptos de fracción propia e impropia.
- Fracciones propias son aquellas cuyo numerador (en valor absoluto) es menor que el denominador (en valor absoluto). Su valor absoluto es menor que 1.
- Fracciones impropias son aquellas que no son propias. Su valor absoluto es mayor que 1.
Representación gráfica de fracciones propias e impropias.
Actividad en la que debes separar las fracciones propias de las impropias
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Forma mixta de una fracción
Las fracciones impropias representan algo mayor que el todo, es decir, cuando trabajamos con una fracción impropia damos a entender que tenemos unidades completas de algo y, posiblemente, alguna unidad incompleta.
Esto queda de manifiesto en la proposición y en los ejemplos que damos a continuación.
Proposición Toda fracción impropia, 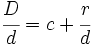
donde Demostración:
|
Ejemplo 1:
La fracción 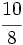 es impropia.
es impropia.
Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 4):
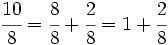
Ejemplo 2:
La frácción 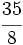 es impropia. La podemos decomponer en la suma de un entero y una fracción propia.
es impropia. La podemos decomponer en la suma de un entero y una fracción propia.
Para ello, dividimos 35 entre 8:
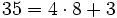
El dividendo 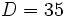 , el divisor
, el divisor 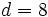 , el cociente
, el cociente 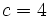 y el resto
y el resto 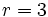 .
.
Aplicando la proposición anterior:
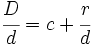
y sustituyendo cada letra por su valor:
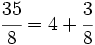
Actividades sobre el signo de las fracciones y sobre la descomposición de fracciones impropias como suma de un entero y una fracción propia.
Números mixtos
Una fracción mixta o número mixto es la representación de una fracción impropia como un número entero más una fracción propia, en la que se omite el signo de suma.
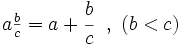
La fracción situada a la derecha del entero suele escribirse con una tipografía de menor tamaño para que no se confunda con una multiplicación de un número por una fracción.
Números mixtos. Ejemplos de paso de forma fraccionaria a mixta y viceversa.
Conversión de fracción impropia a número mixto
Conversión de fracción impropia a número mixto.
Conversión de fracción impropia a número mixto.
Escribiendo una fracción impropia com un número mixto
Convierte a número mixto la siguiente fracción impropia: 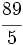
Nota: En el video, la división está realizada por el método anglosajón
Convierte a número mixto la siguiente fracción impropia: 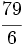
Nota: En el video, la división está realizada por el método anglosajón
Conversión de número mixto a fracción impropia
Conversión de número mixto a fracción impropia.
Conversión de número mixto a fracción impropia.
Convierte a fracción impropia el siguiente número mixto: 
Nota: En el video, la división está realizada por el método anglosajón
Convierte a fracción impropia el siguiente número mixto: 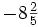
Nota: En el video, la división está realizada por el método anglosajón
Números mixtos y fracciones impropias.
Actividades de nivel variable en las que deberás obtener la forma mixta de una fracción.
|
Calculadora: Fracciones mixtas |
Representación de fracciones en la recta numérica
La representación de números enteros en la recta es algo muy sencillo. Como los enteros son "completos", la distancia entre dos consecutivos siempre es la misma, por lo que basta con escoger esa distancia para nuestra representación. Así, sí quisiésemos situar el número 7, por ejemplo, sólo tendríamos que contar siete saltos hacia la derecha desde el 0. Si quisiésemos representar un número negativo, los saltos serían hacia la izquierda del 0.
Sin embargo, para las fracciones no resulta tan sencillo, porque pueden representar cantidades que no son "completas" y hay que tener mucho cuidado con las distancias que se marcan.
Entonces, ¿cómo representamos una fracción en la recta? Para las fracciones propias es muy sencillo y para las impropias, basta con descomponerlas en parte entera más fracción propia.
Representación de fracciones en la recta numérica
- Si la fracción representa un número entero (el cociente entre numerador y denominador es exacto), la representaremos como tal. (Ver: Números enteros).
- Si la fracción es propia y positiva, se divide el segmento unidad de extremos 0 y 1, en tantas partes iguales como indique el denominador y contamos, desde el 0 hacia la derecha, tantas de esas partes iguales como indique el numerador.
- Si la fracción es propia y negativa, se divide el segmento unidad de extremos -1 y 0, en tantas partes iguales como indique el denominador y contamos, desde el 0 hacia la izquierda, tantas de esas partes iguales como indique el numerador.
- Si la fracción es impropia y positiva, se expresa en la forma
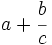 ("valor entero" + "fracción propia") y dividimos el segmento de extremos a y a+1 en c partes iguales y contamos, desde el punto a, hacia la derecha, b de esas partes iguales.
("valor entero" + "fracción propia") y dividimos el segmento de extremos a y a+1 en c partes iguales y contamos, desde el punto a, hacia la derecha, b de esas partes iguales.
- Si la fracción es impropia y negativa, se expresa en la forma
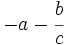 ("-valor entero positivo" - "fracción propia de números positivos") y dividimos el segmento de extremos -(a+1) y -a en c partes iguales y contamos, desde el punto -a, hacia la izquierda, b de esas partes iguales.
("-valor entero positivo" - "fracción propia de números positivos") y dividimos el segmento de extremos -(a+1) y -a en c partes iguales y contamos, desde el punto -a, hacia la izquierda, b de esas partes iguales.
Para dividir un segmento en parte iguales podemos utilizar el Teorema de Thales. Puedes verlo en el siguiente video:
En este vídeo aplicaremos el Teorema de Tales para dividir un segmento en partes iguales.
Ejemplo: Representación de fracciones en la recta numérica
Representa las fracciones:
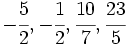
Nota: Pasa las fracciones impropias a forma mixta.
Tutorial que explica el concepto de fracción y su representación gráfica, en partes de la unidad y en la recta numérica.
- 00:00 a 04:14: Conceptos básicos. Ejemplos introductorios.
- 04:14 a 05:38: Definición matemática de fracción.
- 05:38 a 09:45: Representación de fracciones como partes de la unidad (Ejemplos).
- 09:45 a 19:26: Representación de fracciones en la recta numérica (Ejemplos).
- 11:25 a 13:45: Aplicación del Teorema de Tales para la división de segmentos en partes iguales.
Representación del conjunto de los racionales en la recta real.
Representación de fracciones en la recta numérica.
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Escribe la fracción que representa cada una de las letras representadas en la recta numérica.
Escribe la fracción que representa cada una de las letras representadas en la recta numérica.
Representa sobre la misma recta las fracciones 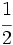 ,
, 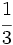 y
y 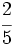 .
.
Representa sobre la misma recta las fracciones 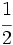 ,
, 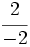 ,
, 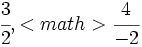 \;</math> y
\;</math> y 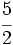 .
.
Representa sobre la misma recta las fracciones 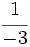 ,
, 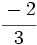 ,
, 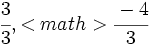 \;</math> y
\;</math> y 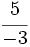 .
.
Representa en la recta real las fracciones 14/5 y -7/4.
Actividad en la que podrás ver como se representan gráficamente fracciones en la recta numérica.
Escribe la fracción impropia que corresponda a cada punto marcado en la recta.
En esta escena podrás comprobar si sabes representar fracciones en la recta numérica.
Haz en tu cuaderno la representación de las siguientes fracciones en la recta numérica:
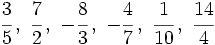
Compruéba las soluciones en la siguiente escena:
Fracciones equivalentes
| El siguiente videotutorial condensa todo lo que se va a ver en este tema sobre fracciones equivalentes:
Tutorial que explica el concepto de fracciones equivalentes y como obtener la fracción irreducible a una dada.
Dos fracciones son equivalentes si tienen el mismo valor. En la Fig.1 tienes ejemplos de fracciones equivalentes. Fíjate como representan la misma porción de la unidad aunque sus numeradores y denominadores sean diferentes.
Introducción a fracciones equivalentes. Modelos de fracciones equivalentes. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe tres fracciones que representen cada uno de los puntos representados en la recta numérica. Escribe las fracciones que representen cada uno de los puntos representados en la recta numérica. ¿Qué puedes decir de esas fracciones? Escribe las fracciones que representen cada uno de los puntos representados en la recta numérica. ¿Qué puedes decir de esas fracciones? Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Indica si las fracciones Calcula cuatro fracciones equivalentes a Calcula cuatro fracciones que representen al número racional |
Obtención de fracciones equivalentes
| Piensa un número. Multiplícalo por 2. Divide el resultado entre 2. ¿Qué sucede?. Lógicamente, el número vuelve a ser el que era al principio porque la multiplicación y la división son operaciones inversas.
Esta idea, junto al hecho de que las fracciones sean el cociente de dos números enteros, permite que muchas fracciones representen el mismo número racional. Más que muchas, infinitas. Piensa, por ejemplo, en la fracción 1/2. Si multiplicamos su numerador y su denominador por el mismo número entero distinto de cero, en realidad, no estamos variando el valor de la fracción. Gráficamente, multiplicar el numerador y el denominador de una fracción por el mismo número significa partir el "todo" que estamos considerando en piezas más pequeñas, pero en realidad no varía la cantidad de ese "todo" que se toma. Fíjate en la animación para entenderlo mejor. |
Obtención de fracciones equivalentes
Si se multiplica o se divide (de forma exacta) el numerador y el denominador de una fracción por un mismo número distinto de cero, se obtiene una fracción equivalente. Si además el número por el que multiplicamos o dividimos es distinto de 1, estos procedimientos reciben el nombre de amplificación y simplificación, respectivamente.
En realidad, estos dos procesos son inversos el uno del otro. La única diferencia importante entre uno y otro es que, mientras la amplificación se puede hacer siempre, la simplificación sólo es posible si el numerador y el denominador tienen un divisor común mayor que 1.
Amplificación
| Simplificación
|
Obtención de fracciones equivalentes: por amplificación y por simplificación.
Obteniendo fracciones equivalentes por simplificación.
Obteniendo fracciones equivalentes por amplificación y simplificación.
Obtén dos fracciones equivalentes a 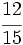 : una por amplificación y otra por simplificación.
: una por amplificación y otra por simplificación.
Escribe tres fracciones equivalentes a 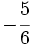 por amplificación.
por amplificación.
Escribe tres fracciones equivalentes a 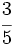 por amplificación.
por amplificación.
Escribe tres fracciones equivalentes a 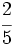 por amplificación.
por amplificación.
Escribe dos fracciones equivalentes a 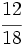 por amplificación.
por amplificación.
Halla una fracción equivalente a 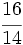 por amplificación y otra por simplificación.
por amplificación y otra por simplificación.
Escribe dos fracciones equivalentes a 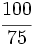 por simplificación.
por simplificación.
Escribe dos fracciones equivalentes a 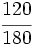 por simplificación.
por simplificación.
Escribe tres fracciones equivalentes a 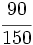 por simplificación.
por simplificación.
Busca una fracción equivalente a la dada con la ayuda del gráfico.
- a) Escribe una fracción equivalente a la dada.
- b) Empareja las fracciones equivalentes.
Fracciones equivalentes. Representación en la recta numérica.
Encontrar fracciones equivalentes por medio de la multiplicación.
Completa la fracción para que se cumpla la igualdad.
Completa la fracción para que se cumpla la igualdad.
Completa la fracción para que se cumpla la igualdad.
Encontrar fracciones equivalentes por medio de la multiplicación.
Simplificación de fracciones
- Simplificar una fracción es sustituirla por otra equivalente con el numerador y denominador menores que los de partida.
- Cuando una fracción no se puede simplificar se dice que es irreducible.
Procedimiento: Simplificación
- Para simplificar fracciones se divide numerador y denominador por un mismo número, distinto de 0 y 1. Este proceso se puede repetir hasta hacer la fracción irreducible.
- Si queremos hacer la fracción irreducible en un solo paso debemos dividir numerador y denominador por el m.c.d. de ambos.
Simplifica 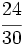 :
:
Solución:
- Paso a paso: Dividimos por 2 y luego por 3
- En un solo paso: Calculamos el m.c.d.(24,30) = 6, y dividimos directamente por 6:
Simplificación de fracciones (3 métodos). Fracción irreducible. Ejemplos.
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: | Simplifica: Simplifica: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: |
- Actividades en las que deberás simplificar fracciones con o sin ayuda.
- Actividad en la que debes emparejar cada fracción con su irreducible.
Actividad en las que deberás encontrar la fracción irreducible.
Actividades de nivel variable en las que deberás simplificar fracciones.
Simplifica fracciones.
La simplificación de fracciones me proporciona un método para saber si dos fracciones son equivalentes.
Procedimiento
Si al simplificar dos fracciones se obtiene la misma fracción irreducible, entonces las dos fracciones son equivalentes.
Determina si 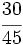 y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
son fracciones equivalentes.
Cómo averiguar si dos fracciones son equivalentes
Con lo que llevamos visto hasta ahora, tenemos dos formas de comprobar que dos fracciones son equivalentes:
- Calculando el valor de cada una de ellas, dividiendo numerador entre denominador, y viendo si el resultado es el mismo.
- Calculando la fracción irreducible de cada una de ellas y viendo si ambas fracciones irreducibles son iguales.
A continuación vamos a ver un resultado que permite hacer la comprobación de forma más simple. Lo llamaremos el método de multiplicar "en cruz".
Comprobación de que dos fracciones son equivalentes
Para saber si dos fracciones son equivalentes, comprobaremos que los productos cruzados de sus numeradores y denominadores coinciden.
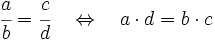
Cómo averiguar el término que falta en una igualdad entre fracciones
Si nos dan dos fracciones equivalentes y en una de ellas desconocemos uno de sus términos, utilizaremos el resultado anterior para averiguarlo.
Cálculo del término desconocido en una proporción. Ejemplos.
- Actividad 2a: Deberás escribir una fracción equivalente a la dada y verás la comprobación por el método de los productos cruzados.
- Actividad 2b: Actividad guiada en la que debes encontrar el término que falta de una igualdad entre fracciones.
Actividad en la que debrás averiguar el término que falta en una igualdad de fracciones.
Actividades
- Escribe, para cada apartado, las tres fracciones equivalentes que resultan de multiplicar el numerado y el denominador de la fracción dada por 2, 3 y 4, en ese orden.
- Encuentra la fracción irreducible para cada apartado.
- De la siguientes parejas de fracciones, señala aquellas que sean equivalentes.
- Completa para que las igualdades sean ciertas.
Ejercicios sobre fracciones equivalentes.
Ejercicios de autoevaluación sobre fracciones propias e impropias, fracciones equivalentes, fracciones irreducibles.
Recucir fracciones a común denominador
Comparar o sumar fracciones nos resultará mucho más fácil si éstas vienen dadas con el mismo denominador. Esto lo podemos conseguir gracias a la equivalencia de fracciones. Lo que tendríamos que hacer sería conseguir, a partir de las fracciones dadas, otras equivalentes pero que tengan el mismo denominador.
Reducir fracciones a común denominador consiste en sustituirlas por otras equivalentes con el mismo denominador.
Procedimiento: Reducir fracciones a común denominador
Para reducir fracciones a común denominador:
- Eligiremos como denominador a un múltiplo común de todos los denominadores. Normalmente se elige el m.c.m. de ellos.
- Amplificamos todas las fracciones para que tengan el mismo denominador, el que acabamos de calcular en el paso anterior. Para ello no tienes más que dividir ese denominador común entre el denominador inicial de la fracción correspondiente y multiplicar el resultado de esa división por el numerador inicial. El resultado de ese producto será el numerador de la fracción amplificada.
Ejemplo: Reducción de fracciones a común denominador
Reduce a común denominador las fracciones: 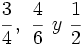
Calculamos el m.c.m. de los denominadores:
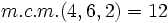 .
.
A continuación, multiplicaremos el numerador y denominador de cada fracción por el resultado de dividir ese m.c.m. por el denominador de cada fracción:
- Reducción de fracciones a comun denominador.
- Reduce a común denominador las siguientes fracciones:
a) 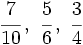
b) 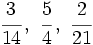
Reducción de fracciones a común denominador.
Reescribe las fraciones 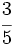 y
y 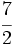 para que tengan denominador 10.
para que tengan denominador 10.
Considera las fraciones 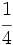 y
y 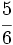 . Reescribe estas fracciones de manera que tengan el mismo denominador. ¿Qué números puedes usar para el denominador: 8, 12, 18, 24?
. Reescribe estas fracciones de manera que tengan el mismo denominador. ¿Qué números puedes usar para el denominador: 8, 12, 18, 24?
Reduce a común denominador 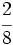 y
y 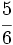 .
.
Reduce a común denominador 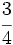 y
y 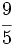 .
.
Reduce a común denominador 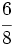 y
y 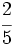 .
.
Reduce a común denominador 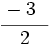 ,
, 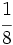 y
y 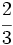 .
.
Reduce a común denominador 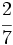 ,
, 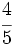 y
y 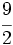 .
.
¿Son equivalentes 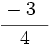 y
y 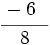 ? Redúcelas a común denominador. ¿Qué ocurre?
? Redúcelas a común denominador. ¿Qué ocurre?
Reduce a común denominador 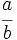 y
y 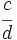 .
.
Actividad en la que verás como de ponen dos fracciones con el mismo denominador y su utilidad para sumar fracciones.
Reducción de fracciones a común denominador.
Reducción de fracciones a común denominador.
Ejercicios de autoevaluación sobre reducción de fracciones a común denominador.
Ejercicios de autoevaluación sobre reducción de fracciones a común denominador.
Ordenación de fracciones
Una forma de comparar fracciones consistía en calcular su valor numérico, efectuando la división. A continuación vamos a ver otras formas distintas de hacerlo. Distinguiremos los siguientes casos:
Caso 1: Las fracciones tienen numeradores o denominadores iguales
En algunos casos es fácil comparar dos fracciones sin necesidad de hacer la división. Esto será posible si ambas fracciones tienen los numeradores o denominadores iguales.
Comparar fracciones con numeradores o denominadores iguales
- De dos fracciones con el mismo denominador, es mayor la de mayor numerador.
- De dos fracciones con el mismo numerador, es mayor la de menor denominador.
Comparando fracciones con mismo denominador o mismo numerador.
Compara fracciones con el mismo numerador o denominador.
Caso 2: Las fracciones tienen numeradores y denominadores distintos
Veamos ahora un procedimiento para los casos en que no sean iguales ni los numeradores ni los denominadores. Lo que haremos será reducirlas a común denominador.
En la animación anterior, cuando los denominadores son distintos, no podemos comparar las piezas coloreadas de verde, pues son de tamaños distintos. Al cambiar los denominadores por 12, sí podemos hacer la comparación. Además, 12 no es un denominador cualquiera, es el mínimo común múltiplo de 3 y 4. Se podría usar cualquier otro múltiplo común, pero lo normal es usar el menor posible para no trabajar con números muy grandes.
Ordenar fracciones
- Para ordenar fracciones con distinto denominador debemos primero reducirlas a común denominador.
- Una vez reducidas a común denominador, será mayor la de mayor numerador.
Ejemplo: Ordenar fracciones
Ordena las siguientes fracciones: 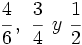
Calculamos el m.c.m. de los denominadores:
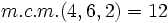 .
.
A continuación, las reducimos a común denominador:
Nótese que hemos multiplicado numerador y denominador por el resultado de dividir el m.c.m. , 12, por cada denominador.
Ordenamos las fracciones obtenidas, y a partir de ellas las fracciones de partida:
Ordena las siguientes fracciones:
a) 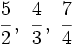
b) 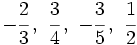
b) 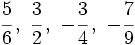
Comparación de fracciones. Ordenar fracciones de forma ascendente. Atención al método usado para obtener el m.c.m. Ordenar fracciones de forma descendente. Compara Compara Compara | Compara Compara Compara Compara las fracciones: Ordena las fracciones: Ordena las fracciones: |
Actividad en la que podrás ver como se comparan fracciones reduciéndolas a común denominador, tanto si son positivas como negativas.
Actividad en la que debes ordenas varias fracciones.
Actividad en la deberás comparar fracciones.
Ejercicios de autoevaluación sobre ordenación y comparación de fracciones.
Ordena fracciones.
Actividades
- Actividad en la que debes ordenas varias fracciones.
- Actividad en la que debes representar varias fracciones en la recta real.
Operaciones con fracciones
Suma y resta de fracciones
Procedimiento: Suma de fracciones
Para sumar o restar fracciones:
- Si las fracciones son homogéneas (mismo denominador), se suman o restan los numeradores y se deja el mismo denominador.
- Si son heterogéneas (distinto denominador), primero se reducen a común denominador y luego se procede como en el caso anterior.
Si en una suma de fracciones alguno de los sumandos es un número entero, se le considerará como si fuera una fracción con denominador unidad.
Cuando hagamos operaciones con fracciones, no sólo la suma y la resta, es posible que el resultado sea una fracción que se pueda simplificar. Es importante que te acostumbres a simplificar el resultado todo lo que sea posible. En la Fig.1, por ejemplo, el resultado que deberíamos dar es 3/4 en lugar de 6/8.
Ejemplo: Suma y resta de fracciones
Calcula: 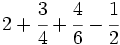
Solución:
Tenemos que calcular:
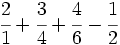
Calculamos el m.c.m. de los denominadores:
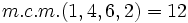
y reducimos las fracciones a común denominador:
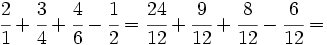
Una vez que tenemos las fracciones homogéneas, sumamos o restamos los númeradores, dejando el mismo denominador:
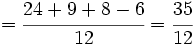
- Suma y resta de fracciones con el mismo denominador.
- Suma y resta de fracciones con el distinto denominador.
- Ejemplos.
Tutorial que explica la suma y resta con fracciones de igual denominador de distintos denominadores y con paréntesis.
- Suma de fracciones con el mismo o con distinto denominador.
- Ejemplos.
- Propiedades.
Suma de fracciones con el mismo denominador. Lo que en este video se explica es válido para la resta sin más que cambiar suma por resta.
Suma de fracciones con el mismo denominador.
Resta de fracciones con el mismo denominador.
Suma de fracciones mixtas con el mismo denominador.
Resta de fracciones mixtas con el mismo denominador.
Suma y resta de fracciones con el mismo denominador:
a) 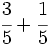 b)
b) 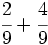 c)
c) 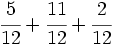 d)
d) 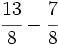 e)
e) 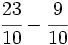
Suma y resta de fracciones con el mismo denominador.
Suma de fracciones usando el método gráfico.
Resta de fracciones usando el método gráfico.
Suma de fracciones usando el método del m.c.m.
Resta de fracciones usando el método del m.c.m.
Suma de números mixtos usando el método del m.c.m.
Resta de números mixtos usando el método del m.c.m.
Suma y resta de fracciones usando el método del m.c.m.
Otro método para sumar o restar fracciones, fácil de recordar, que no requiere del m.c.m, pero que a veces precisa simplificar más al final. Lo que en este video se explica es válido para la resta sin más que cambiar suma por resta.
Suma y resta de fracciones con distinto denominador (método rápido) Suma y resta de fracciones con distinto denominador (método del m.c.m.): a) Suma de fracciones con distinto denominador (método rápido): a) b) Resta de fracciones con distinto denominador (método rápido): a) b) Suma de fracciones con distinto denominador (método del m.c.m.): a) Suma y resta de fracciones con distinto denominador (método del m.c.m.): Suma y resta de fracciones con distinto denominador (método del m.c.m.): Suma y resta de fracciones con distinto denominador:
Suma y resta de fracciones con distinto denominador (método rápido): | Suma y resta de cuatro fracciones con distinto denominador(método del m.c.m.): Suma de un entero y una fracción: Resta de un entero y una fracción. Suma de números mixtos. Resta de números mixtos. Suma y resta de números mixtos. Calcula: Calcula: |
Si Fernando recoge 3/4 de kilo de verdura y David recoge 1/8 de kilo de verdura, calcula los kilos de verdura que han recogido entre los dos e indica aquél que ha recogido menos cantidad.
Suma de fracciones por el método del m.c.m.
Suma y resta de fracciones por el método del m.c.m.
Suma y resta de fracciones. Propiedades.
Suma y resta de fracciones con o sin paréntesis.
Opuesta de una fracción
- Dos fracciones son opuestas cuando su suma es cero.
- Dada una fracción
 , su opuesta es la fracción
, su opuesta es la fracción 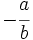 .
.
Multiplicación y división de fracciones
Videotutorial sobre la multiplicación y división de fracciones.
Tutorial que explica la multiplicación y división con fracciones de manera simple y en forma combinada, trabajando la simplificación previa.
Actividades en las que aprenderás la multiplicación de fracciones y sus propiedades.
Multiplicación de fracciones
Procedimiento: Multiplicación de fracciones
Para multiplicar fracciones, se pone como numerador, el producto de los numeradores, y como denominador, el producto de los denominadores.
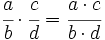
- Si en una multiplicación de fracciones alguno de los sumandos es un número entero, se le considerará como si fuera una fracción con denominador unidad.
- La regla de los signos que utilizabamos para multiplicar números enteros sigue siendo válida con fracciones
Es recomendable, al igual que con cualquier otra operación, simplificar el resultado final, sin embargo, la forma en que se realiza el producto de dos fracciones permite, en ocasiones, simplificar antes de realizar las multiplicaciones de los numeradores y denominadores. Así ahorraras tiempo no teniendo que simplificar posteriormente.
Ejemplo: Multiplicación de fracciones
Calcula: 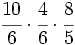
Solución:
Multiplicamos numeradores y denominadores, simplificando antes de efectuar el producto: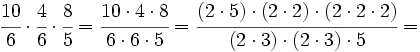
Aprende a multiplicar fracciones.
Aprende a multiplicar fracciones.
Aprende a multiplicar números naturales por fracciones.
Significado gráfico de la multiplicación de dos fracciones.
Representación en la recta numérica de la multiplicación de dos fracciones.
Aprende a multiplicar números por fracciones.
- Multiplicación de fracciones.
- Ejemplos.
- Propiedades.
Multiplica:
Multiplica:
a) 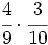 b)
b) 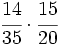 c)
c) 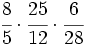
Multiplica un entero por una fracción:
a) 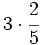
b) 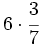
Multiplica fracciones mixtas con fracciones y enteros:
Multiplica:
Compara las siguientes fracciones sin hacer la multiplicación:
Multiplica:
Para elaborar cierto pastel, la receta dice que por cada libra se debe usar 1 taza y 3/4 de almendras. Si nos encargan un pastel de 3 libras y media, ¿cuántas tazas de almendras son necesarias?
Una receta para pastelillos de plátano y avena requiere 3/4 tazas de avena. Si preparamos 1/2 de la receta, ¿cuánta avena necesitaremos?
Gina tenía 2/3 de taza de detergente. Si usó la mitad el viernes para lavar todas sus sábanas, ¿Cuánto le sobra?.
Puedes andar en bicicleta 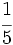 de milla por minuto. Si tardas
de milla por minuto. Si tardas 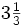 de minuto en llegar a la casa de tu amigo, ¿Cuál es la distancia entre tu casa y la suya?.
de minuto en llegar a la casa de tu amigo, ¿Cuál es la distancia entre tu casa y la suya?.
Actividades en las que aprenderás y practicarás la multiplicación de fracciones.
Actividades para practicar la multiplicación de fracciones.
Inversa de una fracción
- Dos fracciones son inversas cuando su producro es la unidad.
- Toda fracción
 , distinta de cero, tiene inversa. Su inversa es la fracción
, distinta de cero, tiene inversa. Su inversa es la fracción 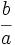 .
.
La inversa de una fracción es otra fracción que al ser multiplicada por ella da la fracción unidad. La fracción que tiene el numerador y denominador intercambiados respecto de ella, es su fracción inversa. Lógicamente, si una fracción es inversa de otra, también son sus inversas todas las equivalentes a esa. La fracción de valor 0 es la única que no tiene inversa.
Marca la fracción inversa, para ello debes marcar primero el numerador, pulsar intro, después el denominador, al pulsar intro te indicará si es CORRECTO o ERROR. Esta actividad no admite rectificaciones, por eso no puedes utilizar los triángulos para variar los números marcados.
Pulsa "inicio" para que aparezca otra fracción.
División de fracciones
Procedimiento: División de fracciones
Para dividir dos fracciones, se multiplica la primera fracción por la inversa de la segunda.
El resultado es otra fracción, cuyo numerador, es el producto del primer numerador por el segundo denominador, y cuyo denominador es el producto del primer denominador por el segundo numerador.
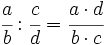
- Si en una división de fracciones alguno de los sumandos es un número entero, se le considerará como si fuera una fracción con denominador unidad.
- La regla de los signos que utilizabamos para dividir números enteros sigue siendo válida con fracciones
Es recomendable, al igual que con cualquier otra operación, simplificar el resultado final, sin embargo, al igual que ocurre con la multiplicación de fracciones, en ocasiones, podremos simplificar antes de efectuar los productos cruzados de los numeradores y denominadores. Lo que haremos es dejar indicados los productos cruzados y simplificarlos, si es posible, antes de multiplicarlos. Así ahorraras tiempo no teniendo que simplificar posteriormente.
Ejemplo:
Calcula: 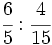
Solución:
Multiplicamos en cruz, simplificando antes de efectuar el producto:Aprende a dividir fracciones.
Aprende a dividir fracciones.
Aprende a dividir fracciones (2 métodos). Ejercicios propuestos y resueltos.
División de dos fracciones usando la fracción inversa. Ejemplos.
- División de fracciones.
- Ejemplos.
- Ejercicios con operaciones combinadas.
División de fracciones. Ejemplo.
Cómo se dividen las fracciones. Ejemplos.
Equivalencias fundamentales en la multiplicación y división de fracciones.
Fracciones de términos no enteros y fracciones de términos racionales
Simplificación de fracciones de términos racionales.
Las propiedades de la división de fracciones
Entendiendo el concepto de división de fracciones
Calcula:
Calcula y expresa la solución como un número mixto:
Calcula:
- 1)
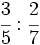 ; 2)
; 2) 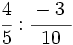 ; 3)
; 3) 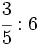 ; 4)
; 4) 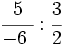
- 5)
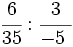 ; 6)
; 6) 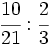 ; 7)
; 7) 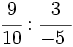
Calcula:
- 8)
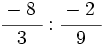 ; 9)
; 9) 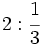 ; 10)
; 10) 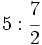
- 11)
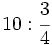 ; 12)
; 12) 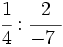 ; 13)
; 13) 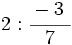
Corrige esta cuenta si crees que es incorrecta:
- 14)
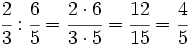
Calcula:
- 15)
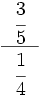 ; 16)
; 16)  ; 17)
; 17) 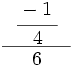 ; 18)
; 18) 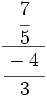
- 19)
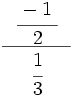 ; 20)
; 20) 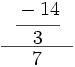 ; 21)
; 21) 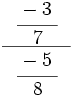
Calcula:
- 22)
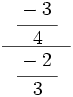 ; 23)
; 23) 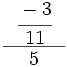 ; 24)
; 24) 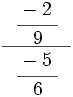
- 25)
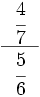 ; 26)
; 26) 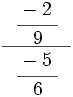 ; 27)
; 27) 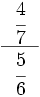
Escribe la fracción que falta para que se verifique la igualdad:
- 52)
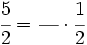
- 53)
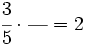
División de fracciones.
a) 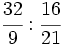 b)
b) 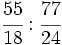
Divide un entero por una fracción:
Divide fracciones mixtas con fracciones:
En la fiesta de cumpleaños de Luisa ha sobrado 1/3 del pastel. Jaime lo ha visto y, como tenía hambre, se ha comido la mitad. ¿Qué parte o fracción de pastel se ha comido Jaime?. ¿Qué parte o fracción del pastel sobra?
La camiseta de un bebe se fabrica con 4/5 metros de tela. ¿Cuántas camisetas se pueden hacer con 48 metros de tela?
Actividades en las que aprenderás y practicarás la división de fracciones.
Actividades para practicar la división de fracciones.
Actividades para practicar la división de fracciones.
Potencia de una fracción
Procedimiento: Potencia de una fracción
Para elevar una fracción a una potencia se eleva el numerador y el denominador a dicha potencia.
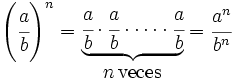
Potencias de exponente negativo
Se define la potencia de exponente negativo como:

Como consecuencia:
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos
Potencias de exponente negativo. Ejemplos.
 . Ejemplos.
. Ejemplos.
Exponentes negativos. Ejemplos.
Razonando sobre el por qué de la definición de los exponentes negativos.
Simplifica:
- a)
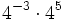
- b)
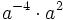
- c)
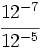
- d)
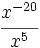
Simplifica:
- a)
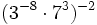
- b)
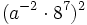
- c)
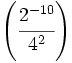
Halla el valor de:
11) 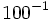 ; 12)
; 12) 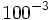 ; 13)
; 13) 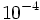 ; 14)
; 14) 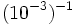
15) 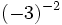 ; 16)
; 16) 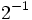 ; 17)
; 17) 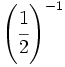 ; 18)
; 18) 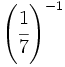 ; 19)
; 19) 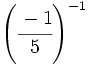
Potencias de exponente negativo.
Actividades sobre potencias de exponente negativo.
Calcula las siguientes potencias y comprueba los resultados en la escena siguiente:
a) 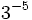 b)
b) 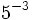 c)
c) 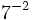 d)
d) 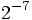
Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba.
Potencias de exponente negativo.
Multiplica y divide potencias (exponentes enteros).
Potencias de productos y cocientes (exponentes enteros)
Potencias de exponentes enteros.
Pulsa el botón "EJERCICIO" y lee atentamente el enunciado. Lo haces en tu cuaderno, escribes la solución en la escena y pulsas el botón "SOLUCIÓN" para ver si lo has hecho bien.
Ejercicios de autoevaluación sobre potencias de exponente negativo.
Propiedades de las potencias de números racionales
Las potencias con números racionales cumplen las mismas propiedades que con números enteros.
Ver: Propiedades de las potencias de números enteros
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
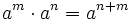
- 2. Cociente de potencias de la misma base:
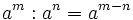
- 3. Potencia de un producto:
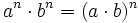
- 4. Potencia de un cociente:
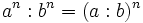
- 5. Potencia de otra potencia:
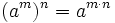
Tutorial que explica la potencia de exponente entero (positivo y negativo) con fracciones y operaciones combinadas con multiplicación, división y potencias, trabajando la simplificación previa.
Simplifica:
- a)
![\left[\left(\cfrac{3}{5} \right)^{-1} \cdot \left(\cfrac{9}{25} \right)^2 \right]^3](/wikipedia/images/math/f/e/c/fec21991837955f9b9d945d4600cba18.png)
- b)
![\left[\cfrac{16}{9} \cdot \left(\cfrac{56}{27} \right)^{-1} \right] \cdot \left(\cfrac{14}{9} \right)^3 \cdot \left(\cfrac{7}{12} \right)^{-2}](/wikipedia/images/math/e/5/1/e5178ed20376c4ef7f07ca88d5d43975.png)
Simplifica 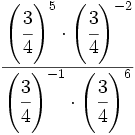
Simplifica: ![\left[ \left( \cfrac{1}{3} \right)^{10} : \left( \cfrac{1}{3} \right)^7 \right]^2](/wikipedia/images/math/6/9/1/6911b07dbbc54e802f87f7498ab77b09.png)
Ejemplos: Potencias de fracciones
Calcula simplificando previamente:
a) 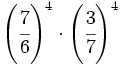 b)
b) 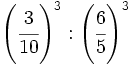 c)
c) 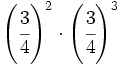
d) 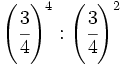 e)
e) 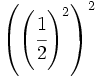 f)
f) 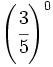
a)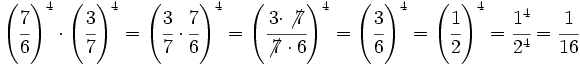
b)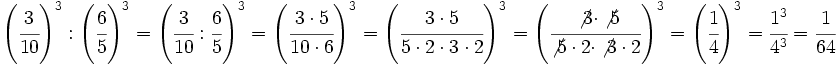
c)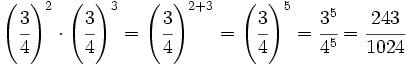
d)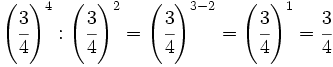
e) 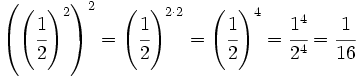
f)
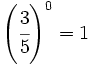
Ejercicios de autoevaluación sobre potencias de fracciones.
Ejercicios de autoevaluación sobre potencias de exponente negativo.
Ejercicios de autoevaluación sobre potencias de números racionales.
Raíces de fracciones
Cómo se calculan las raíces de fracciones. Ejemplos.
Cómo se suman y restan las raíces de fracciones. Ejemplos.
Cómo se multiplican raíces de fracciones. Ejemplos.
Cómo se dividen raíces de fracciones. Ejemplos.
Cómo se calculan las potencias de raíces de fracciones. Ejemplos.
Cómo se calculan las raíces de raíces de fracciones. Ejemplos.
Suma y resta de raíces de fracciones:
- 1)
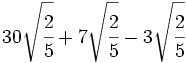
- 2)
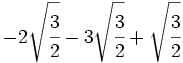
- 3)
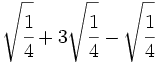
- 4)
![-\cfrac{1}{2}\sqrt[3]{\cfrac{-2}{3}}+\sqrt[3]{\cfrac{-2}{3}}-\cfrac{1}{4}\sqrt[3]{\cfrac{-2}{3}}](/wikipedia/images/math/f/5/5/f55a7abe041410d0d772b3f5f9249888.png)
- 5)
![-8\sqrt[3]{\cfrac{-3}{5}}+\cfrac{3}{2}\sqrt[3]{\cfrac{-3}{5}}-\cfrac{1}{4}\sqrt[3]{\cfrac{-3}{5}}](/wikipedia/images/math/c/7/e/c7e1346a8d6ef7ddeb7f7c7972383303.png)
Suma y resta de raíces de fracciones:
- 6)
![\sqrt[3]{\cfrac{-2}{3}}-\cfrac{1}{2}\sqrt[3]{\cfrac{-2}{3}}+2\sqrt[3]{\cfrac{-2}{3}}](/wikipedia/images/math/e/7/4/e74f2414908471712a21bcd2c0727973.png)
- 7)
![\sqrt[8]{\cfrac{9}{4}}+12\sqrt[8]{\cfrac{9}{4}}-\cfrac{1}{4}\sqrt[8]{\cfrac{9}{4}}](/wikipedia/images/math/7/9/5/7956651986adce493726a51fce226382.png)
- 8)
![\cfrac{-1}{3}\sqrt[11]{\cfrac{-3}{7}}+\cfrac{1}{9}\sqrt[11]{\cfrac{-3}{7}}-\cfrac{2}{3}\sqrt[11]{\cfrac{-3}{7}}](/wikipedia/images/math/f/c/e/fceb6863061e8ca281259ac86890e169.png)
- 9)
![-\sqrt[5]{\cfrac{5}{3}}-\cfrac{5}{2}\sqrt[5]{\cfrac{5}{3}}-\cfrac{1}{4}\sqrt[5]{\cfrac{5}{3}}](/wikipedia/images/math/9/2/2/92245797897977068795b35dc3cbcfc7.png)
Multiplicaciones de raíces de fracciones:
- 10)
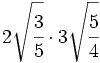
- 11)
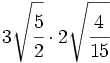
- 12)
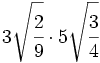
- 13)
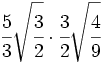
Multiplicaciones de raíces de fracciones:
- 14)
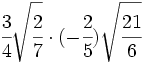
- 15)
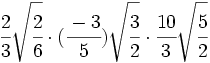
- 16)
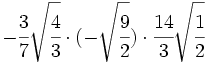
Multiplicaciones de raíces de fracciones:
- 17)
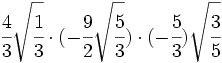
- 18)
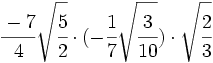
- 19)
![2\sqrt[3]{\cfrac{2}{5}} \cdot 3\sqrt[3]{\cfrac{4}{25}}](/wikipedia/images/math/f/8/1/f81614b373a70320fa5bbee491ded79d.png)
- 20)
![\sqrt[3]{\cfrac{9}{2}} \cdot \cfrac{5}{6}\sqrt[3]{\cfrac{2}{125}}](/wikipedia/images/math/f/d/b/fdbcdfd572102f2971190e92ad2b9ca8.png)
Multiplicaciones de raíces de fracciones:
- 21)
![\cfrac{-2}{5}\sqrt[3]{\cfrac{-1}{3}} \cdot 5\sqrt[3]{\cfrac{-1}{9}}](/wikipedia/images/math/e/1/d/e1dc683585b12c3e8f8b0336e6cd3dce.png)
- 22)
![2\sqrt[3]{\cfrac{7}{3}} \cdot \cfrac{1}{4}\sqrt[3]{\cfrac{9}{14}}](/wikipedia/images/math/4/e/5/4e5561c3d3d0f4cadb26ebea76193f5e.png)
- 23)
![8\sqrt[3]{\cfrac{3}{7}} \cdot \sqrt[3]{\cfrac{-7}{9}} \cdot \sqrt[3]{\cfrac{-7}{2}}](/wikipedia/images/math/9/9/9/99904e001c4c05d9a33cc7f20320c6eb.png)
Multiplicaciones de raíces de fracciones:
- 24)
![3\sqrt[3]{\cfrac{9}{4}} \cdot \left( -\cfrac{1}{2}\sqrt[3]{\cfrac{3}{2}} \right) \cdot \cfrac{2}{5}\sqrt[3]{125}](/wikipedia/images/math/d/3/c/d3cb69b0f72a7fed15f71aa8513dfbb6.png)
- 25)
![\cfrac{4}{3}\sqrt[4]{\cfrac{3}{7}} \cdot 3\sqrt[4]{\cfrac{16}{3}}](/wikipedia/images/math/b/d/5/bd5b5b76b496c2f6825e62489c158052.png)
- 26)
![\cfrac{1}{3}\sqrt[8]{\cfrac{1}{4}} \cdot \left( -\cfrac{9}{2}\sqrt[8]{\cfrac{2}{3}} \right) \cdot 4\sqrt[8]{\cfrac{3}{5}}](/wikipedia/images/math/7/4/4/74408c6f3e91a102054dcf8b4a208595.png)
División de raíces de fracciones:
- 27)
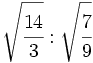
- 28)
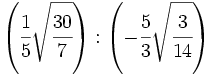
- 29)
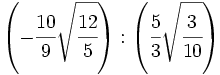
- 30)
![\left( -\cfrac{2}{3}\sqrt[3]{\cfrac{14}{5}} \right): \left( \cfrac{14}{12}\sqrt[3]{\cfrac{7}{10}} \right)](/wikipedia/images/math/a/9/1/a913d1108fd67aec4f52e62b81efa9e8.png)
División de raíces de fracciones:
- 31)
![\left( \cfrac{9}{2}\sqrt[3]{\cfrac{14}{9}} \right) : \left( \sqrt[3]{\cfrac{-7}{3}} \right)](/wikipedia/images/math/8/9/e/89e41ac40d647d9d9d10fd9f080b8f9c.png)
- 32)
![\left( \cfrac{12}{5}\sqrt[3]{\cfrac{18}{3}} \right): \left( -\cfrac{6}{5}\sqrt[3]{\cfrac{-9}{2}} \right)](/wikipedia/images/math/7/8/b/78b4e0f5d87c167f3b7d0e410f45c6ec.png)
División de raíces de fracciones:
- 33)
![\left( -\cfrac{10}{3}\sqrt[4]{\cfrac{15}{49}} \right) : \left( \cfrac{5}{27}\sqrt[4]{\cfrac{49}{125}} \right)](/wikipedia/images/math/a/6/4/a64ae58b74db2719880d0c4bceb986c7.png)
- 34)
![\left( -\cfrac{10}{4}\sqrt[5]{\cfrac{15}{7}} \right): \left( \cfrac{5}{6}\sqrt[5]{\cfrac{5}{14}} \right)](/wikipedia/images/math/9/4/7/9479dbe129a893330d386ef04c8dddcb.png)
- 35)
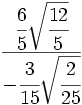
División de raíces de fracciones:
- 36)
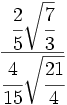
- 37)
![\cfrac{-\cfrac{10}{7}\sqrt[3]{\cfrac{15}{4}}}{5\sqrt[3]{\cfrac{8}{9}}}](/wikipedia/images/math/3/f/7/3f7ec32f3c77881d616b8760375d4d6f.png)
- 38)
![\cfrac{-\cfrac{10}{6}\sqrt[3]{\cfrac{15}{4}}}{\cfrac{5}{3}\sqrt[3]{\cfrac{2}{25}}}](/wikipedia/images/math/2/f/5/2f578dac94a33d0ddc501f0c60f4fffb.png)
Potencias de raíces de fracciones:
- 39)
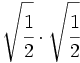
- 40)
![\sqrt[3]{\cfrac{-1}{5}} \cdot \sqrt[3]{\cfrac{-1}{5}} \cdot \sqrt[3]{\cfrac{-1}{5}}](/wikipedia/images/math/6/3/9/63995d3707778bdb86de378c75aca586.png)
- 41)
![\sqrt[3]{\cfrac{2}{3}} \cdot \sqrt[3]{\cfrac{2}{3}} \cdot \sqrt[3]{\cfrac{2}{3}}](/wikipedia/images/math/6/3/3/633c62efe0db98851d8196c7d058cbe0.png)
- 42)
![\sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}} \cdot \sqrt[4]{\cfrac{3}{5}}](/wikipedia/images/math/9/0/e/90e63a779d9f738b1332ad73f20d0c44.png)
- 43)
![\sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}} \cdot \sqrt[6]{\cfrac{3}{2}}](/wikipedia/images/math/9/f/0/9f0f9afc0dba273231a5b490e098027d.png)
Convierte en potencias de exponente fraccionario:
- 44)
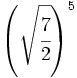 ; 45)
; 45) 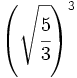 ; 46)
; 46) 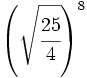
- 47)
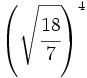 ; 48)
; 48) 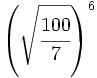 ; 49)
; 49) ![\left( \sqrt[3]{\cfrac{7}{3}} \right)^6](/wikipedia/images/math/7/6/3/763844586d27849f01b0f220f197d4d0.png)
- 50)
![\left( \sqrt[3]{\cfrac{5}{2}} \right)^9](/wikipedia/images/math/5/b/7/5b7af58a06ea229f4169c8f038eeb6a0.png) ; 51)
; 51) ![\left( \sqrt[4]{\cfrac{7}{4}} \right)^8](/wikipedia/images/math/0/e/0/0e0e0fafb99b320da94e2293f4f14701.png) ; 52)
; 52) ![\left( \sqrt[6]{\cfrac{21}{5}} \right)^{12}](/wikipedia/images/math/a/0/7/a07d93d0c3029249c9933a99a2eb2728.png)
- 53)
![\left( \sqrt[21]{\cfrac{12}{5}} \right)^{14}](/wikipedia/images/math/5/5/3/55309d54139afb8fbea7172261e4f109.png)
Convierte la potencia en raíz:
- 54)
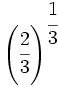 ; 55)
; 55) 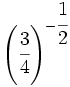 ; 56)
; 56) 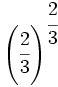
- 57)
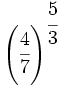 ; 58)
; 58) 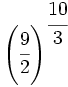 ; 59)
; 59) 
Raíces de una raíz de una fracción:
- 60)
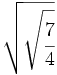 ; 61)
; 61) 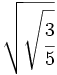 ; 62)
; 62) 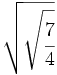
- 63)
![\sqrt[3]{\sqrt{\cfrac{2}{5}}}](/wikipedia/images/math/f/e/9/fe9d5ed19933ef100bc8b0f67559fa52.png) ; 64)
; 64) ![\sqrt[3]{\sqrt[3]{\cfrac{25}{4}}}](/wikipedia/images/math/7/b/3/7b3a4b58a2b91246bf250ff1abd743b3.png) ; 65)
; 65) ![\sqrt{\sqrt[3]{64}}](/wikipedia/images/math/0/e/d/0eddc7f2593e00fd623113cf77aff52f.png)
- 66)
![\sqrt[4]{\sqrt[3]{\cfrac{2}{7}}}](/wikipedia/images/math/e/b/e/ebedfae4b0471be70ea604bbe26e5e19.png) ; 67)
; 67) ![\sqrt[3]{\sqrt{\cfrac{12}{5}}}](/wikipedia/images/math/2/f/5/2f5c1b5dfc0e771272ee1b0c8e2ac6db.png)
Racionalización
Ver: Racionalización
Operaciones combinadas con fracciones
A la hora de operar con fracciones seguiremos las mismas pautas que con números enteros:
Ver: Jerarquía de las operaciones con números enteros
Jerarquía de las operaciones
A la hora de operar seguiremos las siguientes pautas:
- Primero se efectúan las operaciones del interior de los paréntesis. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
- Dentro de los paréntesis, o una vez quitados todos los paréntesis, las operaciones se efectúan en el siguiente orden:
- Las potencias y las raíces.
- Las multiplicaciones y las divisiones (de izquierda a derecha).
- Las sumas y las restas.
- Cuando aparecen paréntesis dentro de otros paréntesis, se puede optar por cambiar los paréntesis más exteriores por corchetes, con el fin de facilitar la lectura de la operación.
- Cuando resuelvas los paréntesis puedes completar las operaciones que encierren o aplicar la propiedad distributiva.
- En cada uno de los pasos que des para resolver una expresión con operaciones combinadas se puede llevar a cabo más de una operación, siempre que no suponga romper el orden que acabamos de establecer.
Ejemplo:
Efectúa las siguientes operaciones combinadas:
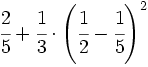
Solución:
- Los paréntesis:
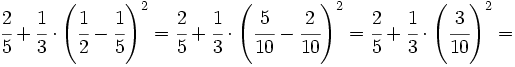
- Las potencias:

- Las multiplicaciones y divisiones:
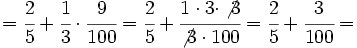
- Las sumas y restas:
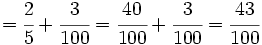
- Finalmente simplificaríamos si pudiésemos. En este caso la fracción es irreducible.
Tutorial que explica las operaciones combinadas con fracciones, señalando el orden que hay que seguir a la hora de realizar las operaciones con números (jerarquía de operaciones).
- 00:00 a 03:28: Conceptos básicos. Jerarquía de operaciones.
- 03:28 a 20:35: 7 Ejercicios de operaciones combinadas.
Operaciones combinadas con fracciones.
Operaciones combinadas con fracciones.
Operaciones combinadas con fracciones.
Opera y simplifica: 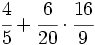
Opera y simplifica: 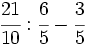
Opera y simplifica:
- a)
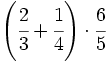
- b)
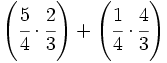
Calcula:
28) 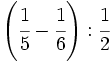
29) 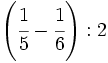
Calcula:
30) 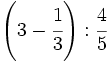
31) 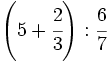
Calcula:
32) 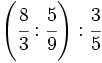
33) 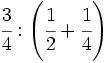
34) 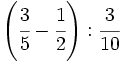
Calcula:
35) 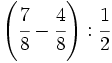
36) 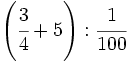
Calcula:
37) 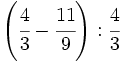
38) 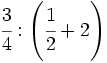
Calcula:
39) 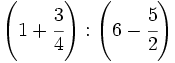 ; 40)
; 40) 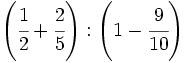 ; 41)
; 41) 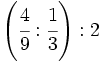
42) 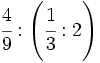 ; 43)
; 43) 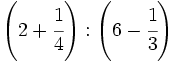
Opera y simplifica: 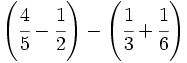
Opera y simplifica: 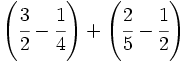
Opera y simplifica números mixtos: 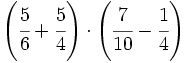
Opera y simplifica: 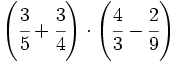
Opera y simplifica: 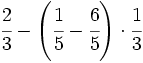
Operaciones combinadas con 3 fracciones sin paréntesis.
Operaciones combinadas con 4 fracciones con o sin paréntesis.
Multiplicaciones, divisiones y operaciones combinadas de fracciones.
Opera y simplifica: ![12- 6 \cdot \left[ \cfrac{1}{3}+\cfrac{5}{7} \left( \cfrac{2}{5}+ \cfrac{3}{10} \right)-2 \right]](/wikipedia/images/math/d/8/a/d8a9f0817768082ad4b67912b5ed86f4.png)
Opera y simplifica: ![\left(\cfrac{2}{5}-\cfrac{1}{2} \right)+ \cfrac{3}{5} \cdot \left[ \cfrac{7}{12}-\cfrac{3}{5} : \left( \cfrac{1}{4}- \cfrac{1}{5} \right) \right]](/wikipedia/images/math/d/7/4/d743f51542cc24868b95259918352133.png)
Opera y simplifica: 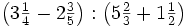
Opera y simplifica: ![\left[ 3 \left\{ 2(2-5)^2-4 \left(\frac{3}{2}-\cfrac{10}{4} \right)^3 \right \} + 3 \cdot \cfrac{7}{9} \right] - \sqrt{49}](/wikipedia/images/math/1/9/0/19095301a9dd1177e424b87facf98fed.png)
Tutorial que explica las operaciones con fracciones en las que intervienen "castillos".
Calcula:
- 44)
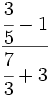 ; 45)
; 45) 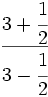 ; 46)
; 46) 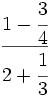
- 47)
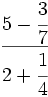 ; 48)
; 48) 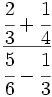
Calcula:
- 49)
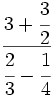 ; 50)
; 50) 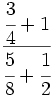 ; 51)
; 51) 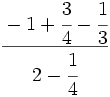
Opera y simplifica: 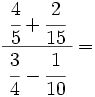
Opera y simplifica: 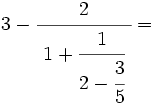
Opera y simplifica: 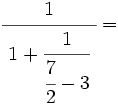
Opera y simplifica: 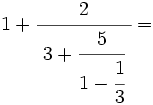
Opera y simplifica: 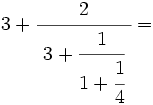
Opera y simplifica: 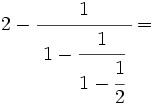
Opera y simplifica: 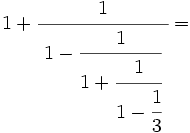
Actividades para aprender y practicar las operaciones combinadas con fracciones (Nivel 3).
Actividades para aprender y practicar las operaciones combinadas con fracciones.
Actividades para aprender y practicar las operaciones combinadas con fracciones. Incluye operaciones con paréntesis implícitos (castillos).
Ejercicios de autoevaluación sobre operaciones combinadas con fracciones.
Ejercicios de autoevaluación sobre operaciones combinadas con fracciones.
Nota: Esta actividad también incluye raíces de fracciones. En el siguiente enlace puedes ver acerca de ellas.
Potencias y raíces de fracciones
La fracción como operador
Para calcular una fracción  de una cantidad
de una cantidad 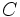 , procederemos multiplicando la fracción por la cantidad:
, procederemos multiplicando la fracción por la cantidad: 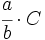
Ejemplos: La fracción como operador
- Un cartero ha de repartir los 3/28 del total de 4004 cartas. ¿Cuántas cartas le correspoden?
- De una herencia de 104000 €, Alberto posee 3/8; Berta, 5/12, y Claudia, el resto. Claudia emplea 2/5 de su parte en pagar deudas. ¿Cuánto le queda?
Solución 1:
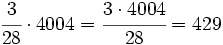 cartas
cartas
Solución 2:
Calculemos primero la fracción correspondiente a Claudia:
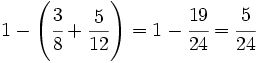
que equivale a:
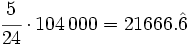 €
€
Claudia emplea en pagar deudas 2/5 de esa cantidad:
 €
€
Restando las dos cantidades anteriores tendremos lo que le queda a Claudia:
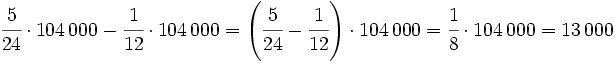 €
€La fracción como operador. Ejemplos.
Tutorial en el que se dan los conceptos matemáticos de proporción y se explica/justifica como calcular proporciones de cantidades o bien la cantidad a la que se le aplicó una proporción.
Cómo se calcula la fracción de un número.
He pagado 2/5 partes de una bici que costaba 90€. ¿Cuánto me falta por pagar?
He pagado 2/5 partes de una bici y me faltan 90€ por pagar. ¿Cuánto costaba la bici?
He pagado 2/5 partes de una bici que suponen 90€ del total. ¿Cuánto costaba la bici?
Ejercicios y problemas
Problemas con fracciones.
Problemas con fracciones.
Problemas para practicar operaciones con fracciones
4 problemas:
- Una caja contiene 60 galletas. Raúl se come 1/3 y Manuel 2/5. ¿Cuántas galletas se ha comido cada uno?
- Pedro ha recorrido en bici 6 km, que son 3/4 de la etapa de hoy. ¿Cuál es el recorrido total de la etapa?
- Alicia tiene 30€ de paga mensual. La primera semana gastó 2/5. La segunda gastó 5/6 de lo que le quedaba. ¿Cuánto gastó cada semana?.¿Cuánto le queda?
- Tenemos que vaciar una piscina. Sacamos por la mañana 2/5 del agua y por la tarde 1/4 de lo que quedaba. Si la final del día había 180 litros, ¿cuál es la capacidad de la piscina?.
2 problemas:
- Tres camiones tienen que trasladar 2400 kg de escombros. El primer camión se lleva 1/3 y después, el segundo, 2/5 del total. ¿Cuánto trasladará el tercero?
- Tres camiones tienen que trasladar 2400 kg de escombros. El primer camión se lleva 1/3 y después, el segundo, 2/5 de lo que queda. ¿Cuánto trasladará el tercero?
Problemas con fracciones.
Problemas con fracciones.
Problemas con fracciones.
Mi padre se ha comido 1/8 de la tableta de turrón y mi madre 2/7 de lo que quedaba. Si costó 4€, ¿cuántos céntimos se comió cada uno?.¿Qué fracción queda?
Problemas resueltos sobre fracciones.
Ejercicios resueltos sobre fracciones.
Expresión decimal de una fracción
El siguiente videotutorial resume gran parte de lo que vamos a ver en este tema.
En este video vamos a ver cómo se transforma una fracción en un número decimal y también cómo se calcula la fracción generatriz de los números decimales.
Para saber más sobre: Números decimales.
Paso de fracción a decimal
Aunque una fracción es un valor exacto y los números decimales a veces requieren tomar aproximaciones, muchas veces resulta más cómodo trabajar con decimales que con fracciones.
Procedimiento
Una fracción se puede expresar como un número decimal calculando su valor, es decir, dividiendo numerador entre denominador.
Tipos de expresiones decimales de una fracción
La expresión decimal de una fracción puede ser:
- Expresión decimal exacta: Si tiene un número finito de decimales.
- Expresión decimal periódica pura: Si tiene un número infinito de decimales que se repiten. La parte que se repite se llama periodo.
- Expresión decimal periódica mixta: Si tiene un número infinito de decimales que se repiten a partir de una cierta posición decimal. La parte que se repite se llama periodo y la parte decimal previa al periodo se llama anteperiodo.
"El número decimal que resulta de dividir el numerador de una fracción entre su denominador es siempre exacto o periódico".
En efecto, piensa en el algoritmo de la división. Si tenemos la suerte de llegar a resto 0, el cociente será un decimal exacto. Si, por el contrario, no conseguimos que el resto sea 0, podemos bajar ceros del dividendo tantas veces como queramos. El asunto es que los restos que pueden aparecer en cada paso tienen que ser menores que el divisor, por tanto, hay un número limitado de restos posibles. Por ejemplo, si dividimos entre 4, los restos podrían ser 0, 1, 2 o 3. Entonces, si seguimos dividiendo (bajando ceros) y no conseguimos que el resto sea cero, en algún momento tendrá que repetirse un resto de entre todos los posibles y el cociente será un decimal periódico.
- Decimal exacto:

- Decimal periódico puro:
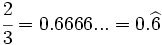 (El periodo es 6)
(El periodo es 6)
- Decimal periódico mixto:
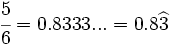 (El anteperiodo es 8 y el periodo es 3)
(El anteperiodo es 8 y el periodo es 3)
Cómo obtener la expresión decimal de una fracción. Ejemplos:
1. a) 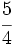 b)
b) 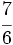
2. a) 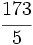 b)
b) 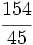 c)
c) 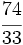
Tutorial en el que se da un rápido repaso a los distintos tipos de decimales y se explica el paso de una fracción a su expresión decimal equivalente (finito o periódico).
Obtén la expresión decimal de 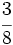
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 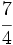
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 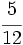
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 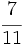
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 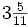
Nota: En el video, la división está realizada por el método anglosajón
Transforma en decimales las siguientes fracciones:
a) 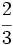 ; b)
; b) 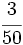 ; c)
; c) 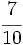 ; d)
; d) 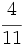 ; e)
; e) 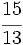
Transforma en decimales las siguientes fracciones:
a) 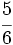 ; b)
; b) 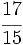 ; c)
; c) 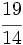 ; d)
; d) 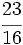
Transforma en decimales las siguientes fracciones decimales:
a) 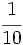 ; b)
; b) 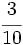 ; c)
; c) 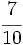 ; d)
; d) 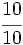 ; e)
; e) 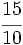 ;
;
f) 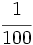 ;g)
;g) 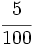 ; h)
; h) 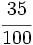 ; i)
; i) 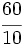 ; j)
; j) 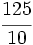 ;
;
k) 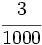 ; l)
; l) 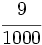 ; m)
; m) 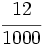 ; n)
; n) 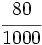 ; o)
; o) 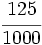 ; p)
; p) 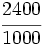
- Actividad en la que podrás ver como se obtiene la expresión decimal de una fracción viendo el desarrollo de la división y los decimales que se obtienen en el cociente.
- Actividad en la que tendrás que elegir qué tipo de expresión decimal es la que te muestran en la escena.
- Fracciones con expresiones decimales exactas.
- Actividad en la que tendrás que elegir qué tipo de expresión decimal es la que te muestran en la escena.
Convertir fracciones a decimales.
Paso de decimal a fracción
Se llama fracción generatriz de un número decimal, a aquella que tiene como valor dicho número decimal.
Toda fracción se puede pasar a forma decimal, sin embargo, lo contrario no es cierto: sólo se pueden pasar a fracción aquellos decimales que sean exactos o periódicos. Cuando el número de decimales es infinito y no periódico (número irracional), como ocurre con el número pi (π), no podemos expresarlo en forma de fracción.
- Actividad en la que podrás ver como se obtiene la fracción generatriz de una expresión decimal exacta, periódica pura o periódica mixta.
- Actividad en la que tendrás que hallar la fracción generatriz de una expresión decimal.
Cómo obtener la fracción generatiz de un número decimal exacto o periódico (2 métodos) con ejemplos:
1. a) 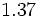 b)
b) 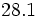 c)
c) 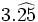 d)
d) 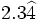
2. a) 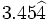 b)
b) 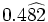 c)
c) 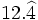
Tutorial en el que se da un rápido repaso a los distintos tipos de decimales y se explica el paso de un número en expresión decimal a su expresión fraccionaria equivalente, tanto en el caso de decimales finitos como periódicos.
Paso de decimal exacto a fracción
La fracción generatriz de un decimal exacto tiene en el numerador la expresión decimal sin la coma, y en el denominador un uno seguido de tantos ceros como cifras decimales.
Es el caso más sencillo. Estos decimales tienen un número finito de cifras decimales. Sólo tenemos que "mover" la coma a la derecha tantos puestos como sea necesario. Para "mover" la coma basta con multiplicar por una potencia de 10. Si queremos mover un puesto, multiplicamos por 10, si son dos puestos, por 100, tres puestos, por 1000... Pero no podemos simplemente multiplicar, porque así cambiaría el valor del número. Hay que "compensar" esa multiplicación con su operación opuesta, la división. Lo que hacemos es poner como denominador la misma potencia de 10 por la que hemos multiplicado el número. Después sólo quedaría simplificar la fracción
También podemos proceder siguiendo el siguiente algoritmo:
- Sea N el número decimal exacto cuya fracción generatriz queremos hallar.
- Multiplicamos N por 10 elevado al número de decimales.
- Despejamos N para obtener la fracción.
Paso de decimal exacto a fracción y su simplificación.
Cómo obtener la fracción generatiz de un número decimal exacto. Ejemplos.
Halla la fracción generatriz de 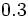
Halla la fracción generatriz de 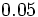
Halla la fracción generatriz de 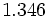
Halla la fracción generatriz de los números:
- a)
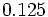
- b)
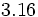
Halla la fracción generatriz de los números:
- a)
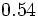 ; b)
; b) 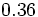 ; c)
; c) 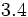 ; d)
; d) 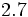 ; e)
; e) 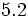 ; f)
; f) 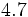 ; g)
; g) 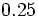 ; h)
; h) 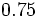 ; i)
; i) 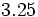 ; j)
; j) 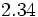 ; k)
; k) 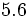 ; l)
; l) 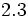 ;
;
Transforma en fracción los siguientes números decimales exactos:
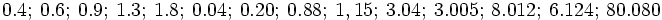
Halla la fracción generatriz de 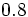
Halla la fracción generatriz de 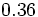
Halla la fracción generatriz de 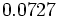
Halla la fracción generatriz de 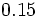
Convierte en número mixto 
Actividad en la que debes pasar de decimal exacto a fracción.
Paso de decimal periódico puro a fracción
La fracción generatriz de un número decimal periódico puro tiene como numerador la diferencia entre a y b, donde a es el número escrito sin la coma (sin repetir el periodo) y b es la parte entera del número; y como denominador, tantos "9" como cifras tiene el periodo.
Este caso es un poco más complicado. Como estos números tienen infinitas cifras decimales, no podemos simplemente "mover" la coma. La idea es buscar otro decimal con el mismo período a partir del decimal que tenemos. Una vez hecho esto, restaremos esos decimales con idéntico período, de forma que el resultado sea un entero. La única "pega" es que tendremos que resolver una pequeña ecuación.
El algoritmo es el siguiente:
- Sea N el número decimal cuya fracción generatriz queremos hallar.
- Multiplicamos N por 10 elevado al número de cifras que tenga el periodo, lo que permite obtener otro número con la misma parte decimal.
- Restamos N y el número obtenido en el paso anterior.
- Despejando N llegamos a la fracción buscada.
Halla la fracción generatriz de los números periódicos puros (2 métodos):
- a) 1.6666...
- b) 2.646464...
Halla la fracción generatriz de número periódico puro 0.3636... (Método largo)
Halla la fracción generatriz de los siguientes números periódicos puros (Método corto):
- a) 0.888...
- b) 0.212121...
- c) 0.537537537...
- d) 2.444...
- e) 10.484848...
Halla la fracción generatriz de los números (Método corto):
- a) 0.363636...
- b) 2.045045...
Halla la fracción generatriz de 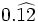 (Método corto)
(Método corto)
Halla la fracción generatriz de 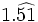 (Método corto)
(Método corto)
Halla la fracción generatriz de 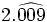 (Método corto)
(Método corto)
Halla la fracción generatriz por el método corto de:
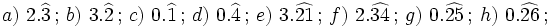
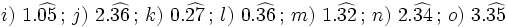
Actividad en la que debes pasar de decimal periódico puro a fracción.
Paso de decimal periódico mixto a fracción
La fracción generatriz de un número decimal periódico mixto tiene como numerador la diferencia entre a y b, donde a es el número escrito sin la coma (sin repetir el periodo) y b es el número escrito sin la coma quitándole la parte decimal periódica. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras tenga el anteperiodo.
Este caso es aún más complicado. La idea es buscar dos decimales con el mismo período a partir del decimal que tenemos. Una vez hecho esto, restaremos esos decimales con idéntico período, de forma que el resultado sea un entero. La única "pega" es que tendremos que resolver una pequeña ecuación.
El algoritmo es el siguiente:
- Sea N el número decimal cuya fracción generatriz queremos hallar.
- Multiplicamos N por 10 elevado al número de cifras que tenga el periodo más el anteperiodo.
- Multiplicamos N por 10 elevado al número de cifras que tenga el anteperiodo, lo que permite obtener otro número con la misma parte decimal que el del paso 2.
- Restamos los números obtenidos en los pasos 2 y 3.
- Despejando N llegamos a la fracción buscada.
Halla la fracción generatriz de los siguientes números periódicos mixtos (2 métodos):
- a) 2.46666...
- b) 3.246262626...
Halla la fracción generatriz de número periódico mixto 0.4333... (Método largo)
Halla la fracción generatriz de los siguientes números periódicos mixtos (Método corto):
- a) 0.5111...
- b) 0.935555...
- c) 3.8121212...
- d) 1.06434343...
Halla la fracción generatriz de los siguientes números periódicos mixtos (Método corto):
- a) 0.3851851...
- b) 4.1244444...
Halla la fracción generatriz de 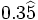 (Método corto)
(Método corto)
Halla la fracción generatriz de 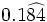 (Método corto)
(Método corto)
Halla la fracción generatriz de 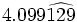 (Método corto)
(Método corto)
Halla la fracción generatriz por el método corto de:
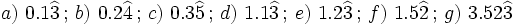
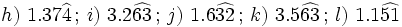
Actividad en la que debes pasar de decimal periódico mixto a fracción.
Ejercicios de autoevaluación sobre fracciones generatrices.
Ejemplos: Paso de decimal a fracción
Expresa en forma de fracción los números decimales:
- a)
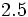
- b)
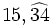
- c)
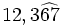
a) 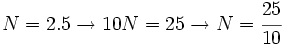
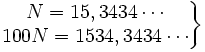 Restando:
Restando: 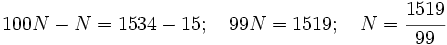 c)
c)  Restando:
Restando: 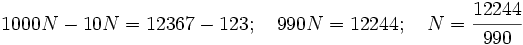
|
Calculadora: Fracciones. Paso a decimal y viceversa |
Actividades
1) Aproxima al entero o decimal exacto más cercano:
a) 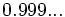 ; b)
; b) 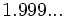 ; c)
; c) 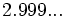 ; d)
; d) 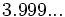 ; e)
; e) 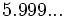 ; f)
; f) 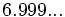 ; g)
; g) 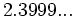 ;
;
h) 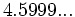 ; i)
; i) 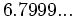 ; j)
; j) 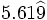 ; k)
; k) 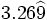 ; l)
; l) 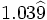
2) Halla las siguiente división: 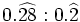 >.
>.
Halla:
- a)
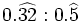
- b)
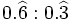
- c)
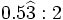
- d)

- e)

Obtención de fracciones generatrices planteando ecuaciones.
Obten la fracción generatriz de un número decimal:
Pulsa el botón "EJERCICIO" para generar una fracción. Debes averiguar de que tipo de expresión decimal se trata sin hacer la división. Luego halla su expresión decimal.
Lo haces en tu cuaderno, escribe la solución en la casilla "Expresión Decimal" y pulsa el botón "SOLUCIÓN" para ver si lo has hecho bien.
Ejercicios y problemas
|
Ejercicios: 1. Agrupa las fracciones que sean equivalentes: Solución: 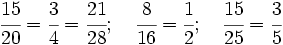 2. Simplifica las fracciones:
Solución: a) 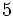 b) b) 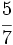 c) c) 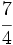 3. Ordena de menor a mayor las fracciones: Solución: 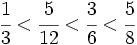 4. Opera las fracciones:
Solución: a) 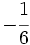 b) b) 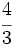 c) c) 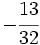 5. Simplifica y expresa en forma de fracción:
Solución: a) 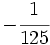 b) b) 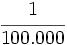 c) c) 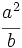 6. Simplifica:
Solución: a) 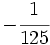 b) b) 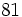 c) c) 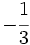 7. Calcula utilizando las propiedades de las potencias:
Solución: 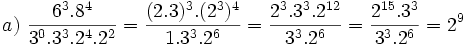
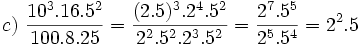 8. Sin hacer la división, indica qué tipo de decimal resulta:
Solución: a) Decimal exacto; b) Decimal periódico puro; c) Decimal periódico mixto. 8. Expresa en forma de fracción:
Solución: a) 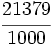 b) b) 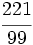 c) c) 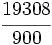 |
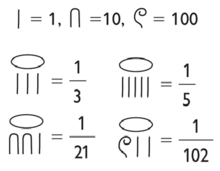
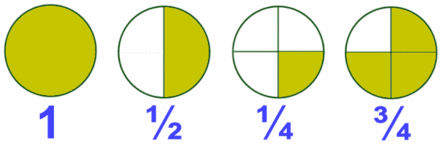
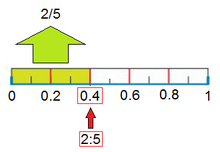
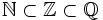
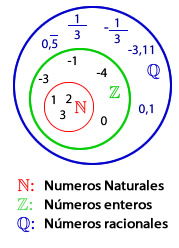
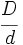 , se puede escribir como suma de un número entero y una fracción propia.
, se puede escribir como suma de un número entero y una fracción propia.
 es el cociente y
es el cociente y  es el resto de la división de
es el resto de la división de  entre
entre  .
.
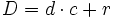
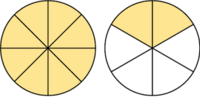
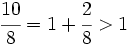
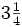 :
:
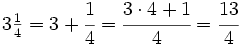
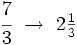 ; B)
; B) 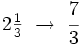
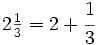
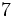

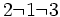 ; B)
; B) 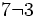
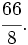
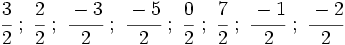
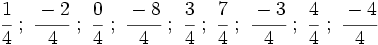
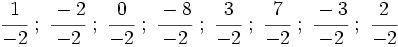
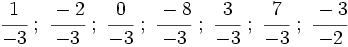
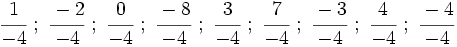
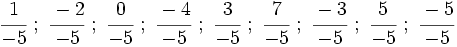
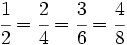
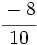 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
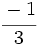 y
y 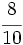 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
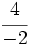 y
y 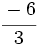 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
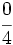 y
y 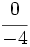 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
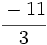 y
y 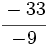 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
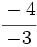 y
y 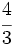 están representadas por el mismo punto sobre la recta numérica y represéntalas.
están representadas por el mismo punto sobre la recta numérica y represéntalas.
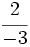 y represéntalas en la recta numérica.
y represéntalas en la recta numérica.
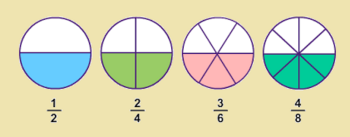
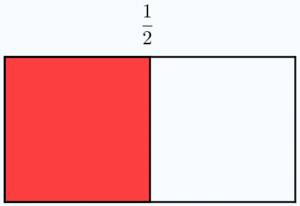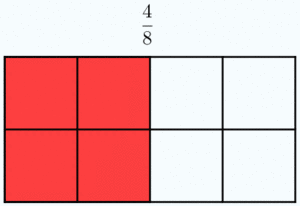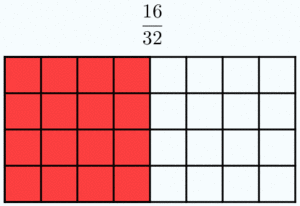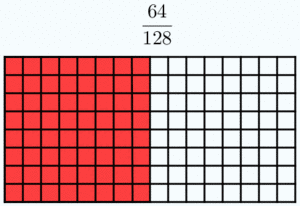
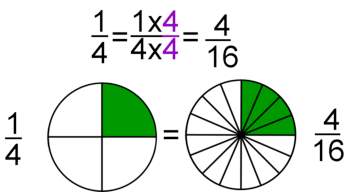
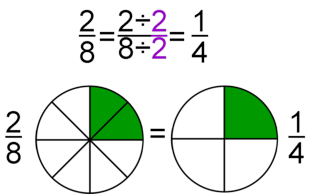
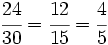
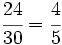
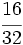 b)
b) 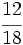
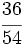 b)
b) 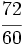
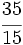 b)
b) 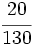
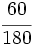 b)
b) 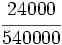
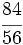 b)
b) 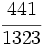
 b)
b) 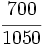
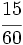
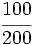 .
.
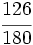 .
.
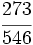 .
.
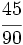 .
.
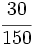 .
.
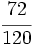 .
.
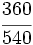 .
.
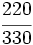 .
.
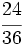 .
.
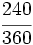 .
.
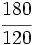 .
.
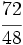 .
.
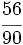 .
.
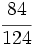 .
.
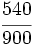 .
.
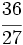 .
.
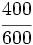 .
.
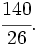
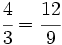 , porque
, porque 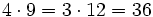 (son equivalentes)
(son equivalentes)
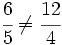 , porque
, porque 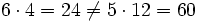 (no son equivalentes)
(no son equivalentes)
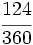 y
y 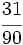 ?
?
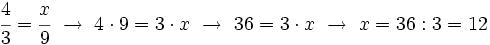
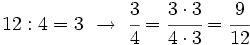
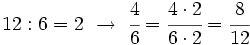
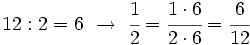
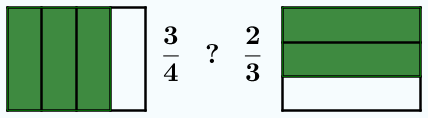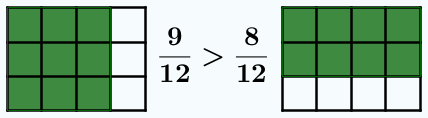
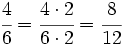
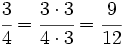
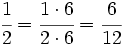
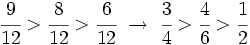
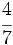 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
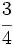 y
y 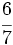 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
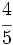 y
y 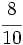 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
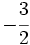 y
y 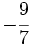 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
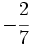 y
y 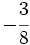 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
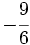 y
y 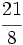 y
y 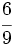 .
.
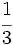 y
y 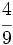 ,
, 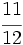 y
y 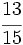 .
.
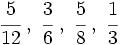
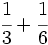 b)
b) 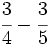
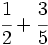
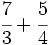
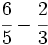

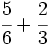 b)
b) 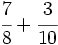 c)
c) 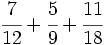
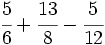
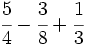
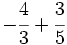

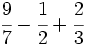
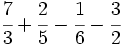
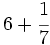
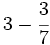
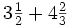
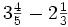
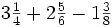
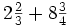
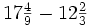
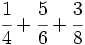
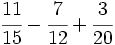
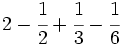
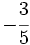 .
.
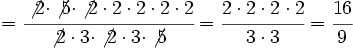
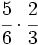
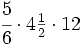
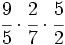
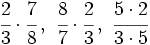
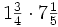
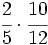
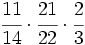
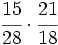
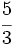 .
.
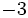 .
.
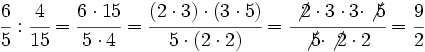
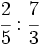
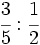
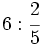
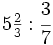
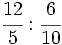
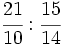
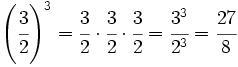
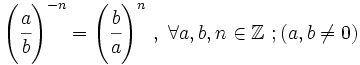
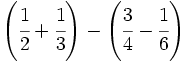 b)
b) 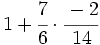 c)
c) 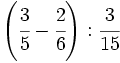
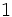
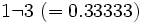
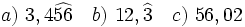
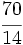 b)
b)  c)
c) 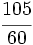
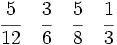
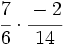 b)
b) 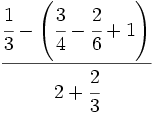
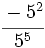 b)
b) 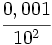 c)
c) 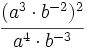
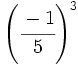 b)
b) ![\left [ \left ( \cfrac{-1}{3} \right )^{-2} \right ]^2](/wikipedia/images/math/1/4/e/14e6c8e9222f905775e21fb947d71f2c.png) c)
c) 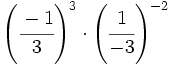
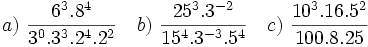
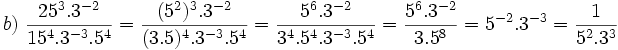
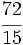 b)
b) 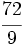 c)
c)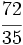
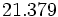 b)
b) 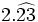 c)
c)