Números enteros
De Wikipedia
| Revisión de 19:04 23 may 2007 Coordinador (Discusión | contribuciones) (→Potencias) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Menú Matemáticas 3ESO | + | {{Menú Matemáticas Contenidos Generales |
| |titulo=NUMEROS ENTEROS | |titulo=NUMEROS ENTEROS | ||
| - | |ir= |ampliar= | + | |ir= |
| + | |ampliar= | ||
| |repasar= | |repasar= | ||
| - | [http://descartes.cnice.mecd.es/1y2_eso/enteros1/index.htm Números enteros I]<br> | + | |enlaces= |
| - | [http://descartes.cnice.mecd.es/1y2_eso/enteros2/index.htm Números enteros II]<br> | + | }} |
| - | [http://descartes.cnice.mecd.es/3_eso/Potencias/ Potencias] | + | {{p}} |
| - | |enlaces=[http://es.wikipedia.org/wiki/Numeros_enteros Números enteros]}}{{p}} | + | =Los números enteros= |
| - | ==Definición== | + | {{Introducción números enteros}} |
| - | {{Caja Amarilla|texto=El conjunto de los '''números enteros''' es | + | {{p}} |
| - | <center><math>\mathbb{Z}=\left \lbrace \cdots, -3, -2,-1,\ 0,\ 1 ,\ 2,\ 3, \cdots \right \rbrace</math></center>}}{{p}}Son infinitos y, al igual que los [[números naturales]] sirven para contar. Sin embargo, los números enteros permiten expresar cantidades negativas como un saldo deudor en una cuenta bancaria, un año de la era antes de Cristo, el número de una planta del sótano de un edificio, etc. | + | ==Números naturales== |
| - | + | Empezaremos recordando primero qué eran los números naturales. | |
| + | {{p}} | ||
| + | {{Def_cto_num_naturales}} | ||
| + | {{p}} | ||
| + | ===Representación de los números naturales=== | ||
| Podemos representarlos en una recta: | Podemos representarlos en una recta: | ||
| - | <center>[[Imagen:recta_enteros.png|500px]]</center> | + | <center>[[Imagen:recta_naturales.png|500px]]</center> |
| {{p}} | {{p}} | ||
| - | + | {{Video: Numeros naturales. Numeros primos}} | |
| - | {{AI2|titulo=Actividades Interactivas: ''Números enteros''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado=1. Introducción al conjunto de los números enteros. | + | |
| - | |actividad= | + | |
| - | En la escena adjunta te presentamos unos ejemplos en los que se muestra la necesidad de utilizar números enteros. | + | |
| - | Sigue las instrucciones que te van apareciendo en escena y anota los ejemplos en tu cuaderno. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/introduccionenteros_1.html | + | |
| - | width=550 | + | |
| - | height=550 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado=2. Representación de los números enteros en la recta numérica. | + | |
| - | |actividad= | + | |
| - | En esta escena vas a conocer como se representan los números enteros en la recta numérica. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/rectanumerica_1.html | + | |
| - | width=100% | + | |
| - | height=500 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| + | ---- | ||
| + | Para más información: [[Números naturales]] | ||
| - | ==Orden== | + | ==Números negativos y positivos== |
| - | En el gráfico anterior se observa el orden que existe en el conjunto de los números enteros, siendo los números negativos menores que los positivos y que el cero. Se cumple que: | + | {{Números negativos y positivos}} |
| - | <center><math>Si\ a<b,\ entonces\ -b<-a\quad \forall\;a,\ b \in \mathbb{N}</math></center> | + | |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas: ''Orden en los números enteros''''|cuerpo= | + | ===Utilidad de los números negativos y positivos=== |
| - | {{ai_cuerpo | + | {{Utilidad de los números negativos y positivos}} |
| - | |enunciado=1. ¿Cómo se ordenan los números enteros?. | + | |
| - | |actividad= | + | |
| - | En esta escena aprenderás a comparar números enteros. Anota lo que aprendas en tu cuaderno. | + | |
| - | + | ||
| - | Lee atentamente las indicaciones. Pulsa INICIO cada vez que quieras ver un ejemplo nuevo. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/ordenenz_1.html | + | |
| - | width=100% | + | |
| - | height=525 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado=2. Autoevaluación. | + | |
| - | |actividad= | + | |
| - | En esta escena deberas decir que número es el mayor. Anota los resultados en tu cuaderno. | + | |
| - | + | ||
| - | Pulsa INICIO cada vez que quieras ver un ejemplo nuevo. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/ordenenz_2.html | + | |
| - | width=500 | + | |
| - | height=325 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | + | ||
| - | }} | + | |
| - | + | ||
| - | ==Operaciones== | + | |
| - | ===Opuesto=== | + | |
| - | El opuesto de un número entero ''a'' es otro número entero ''-a''. | + | |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Opuesto de un número entero''''|cuerpo= | + | ==Números enteros== |
| - | {{ai_cuerpo | + | {{Números enteros 1ºESO}} |
| - | |enunciado=1. Calcula el opuesto de un número entero. | + | |
| - | |actividad= | + | |
| - | Cambia, utilizando el pulsador, los valores y contesta en tu cuaderno las siguientes preguntas: | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/opuesto_1.html | + | |
| - | width=450 | + | |
| - | height=300 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | a) ¿Cuál es el opuesto de cero?{{p}} | + | |
| - | b) Si el número es negativo ¿qué signo tiene su opuesto?{{p}} | + | |
| - | c) Si el número es positivo ¿qué signo tiene su opuesto? | + | |
| - | + | ||
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | + | ===Representación de los números enteros=== | |
| - | ===Valor absoluto=== | + | {{Representación de los números enteros 1ºESO}} |
| - | {{Caja Amarilla|texto=El '''valor absoluto''' de un número entero ''a'' es su magnitud, prescindiendo del signo. Se escribe <math>|a|\;\!</math> y se define del siguiente modo: | + | |
| - | <center><math>|a|= \begin{cases} \ \ a & \mbox{si }a>0 \\ -a & \mbox{si }a<0 \end{cases}</math></center>}} | + | |
| {{p}} | {{p}} | ||
| - | Por ejemplo, <math>|-3|=3 \,\!</math> y <math>|5|=5 \,\!</math>.<br> | + | ===Valor absoluto de un entero=== |
| - | + | {{Valor Absoluto Entero}} | |
| - | {{AI2|titulo=Actividad Interactiva: ''Valor absoluto de un número entero''''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado=1. Calcula el valor absoluto de un número entero. | + | |
| - | |actividad= | + | |
| - | Cambia, utilizando el pulsador, los valores y contesta en tu cuaderno las siguientes preguntas: | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/valorabs_1.html | + | |
| - | width=450 | + | |
| - | height=300 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | Contesta en tu cuaderno las siguientes preguntas: | + | |
| - | + | ||
| - | a) ¿Cuál es el valor absoluto de cero?{{p}} | + | |
| - | b) ¿Qué signo tiene el valor absoluto de un número negativo? ¿Y de uno positivo? | + | |
| - | c) ¿El valor absoluto de un número puede ser negativo? | + | |
| - | + | ||
| - | + | ||
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | + | ===Opuesto de un entero=== | |
| - | ===Suma y resta=== | + | {{Opuesto de un entero}} |
| - | La '''suma''' de números enteros es otro número entero. La '''resta''' de números enteros es otro número entero resultado de sumar el primero con el opuesto del segundo. | + | |
| - | + | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Suma de números enteros''''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado=1. Practica la suma de números enteros. | + | |
| - | |actividad= | + | |
| - | Introduce el resultado con el teclado y pulsa "intro". | + | |
| - | Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. | + | |
| - | + | ||
| - | * '''Suma de dos números enteros:''' | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/enteros1_1.html | + | |
| - | width=450 | + | |
| - | height=300 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | * '''Suma de tres números enteros (Agrupando los que tienen el mismo signo):''' | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/enteros1_2.html | + | |
| - | width=450 | + | |
| - | height=300 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | * '''Suma de tres números enteros (Agrupandolos de dos en dos):''' | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/enteros1_3.html | + | |
| - | width=450 | + | |
| - | height=300 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | + | ===Orden en el conjunto de los enteros=== | |
| - | ===Jerarquía de las operaciones=== | + | {{Orden en el conjunto de los enteros}} |
| - | Al operar con números enteros se atiende a la misma [http://maralboran.ath.cx/wikipedia/index.php/N%C3%BAmeros_naturales#Jerarqu.C3.ADa_de_las_operaciones jerarquia de las operaciones con naturales].{{p}} | + | |
| - | {{AI2|titulo=Actividad Interactiva: ''''Uso del paréntesis''''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado=1. Operaciones con paréntesis: | + | |
| - | |actividad= | + | |
| - | Introduce el resultado con el teclado y pulsa "intro". | + | |
| - | Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. | + | |
| - | + | ||
| - | * '''Operaciones sencillas con paréntesis:''' | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/parentesis_1.html | + | |
| - | width=550 | + | |
| - | height=400 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | * '''Más operaciones con paréntesis:''' | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/parentesis_2.html | + | |
| - | width=650 | + | |
| - | height=400 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado=2. Operaciones combinadas: | + | |
| - | |actividad= | + | |
| - | En esta actividad debes marcar en la ventana bajo la escena el número que sigue al resolver la expresión. Cuando el número marcado sea el correcto aparecerá en la escena, si no es el correcto no aparecerá. | + | |
| - | + | ||
| - | Debes hacerlo sucesivamente, paso a paso, para ello debes borrar el número anterior. No se trata de que halles directamente el resultado final. | + | |
| - | + | ||
| - | Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. | + | |
| - | + | ||
| - | {{Caja|contenido=<iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enteros2/opcombin_1.html | + | |
| - | width=450 | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe>}} | + | |
| - | }} | + | |
| - | }} | + | |
| - | + | ||
| {{p}} | {{p}} | ||
| - | + | ==Actividades== | |
| - | ===Multiplicación=== | + | {{Actividades: numeros enteros}} |
| - | ====Regla de los signos==== | + | |
| - | Si dos números enteros tienen el mismo signo su producto es un entero positivo. Y si tienen distinto signo, el producto es un entero negativo. Ésto es: | + | |
| - | {{caja|contenido= | + | |
| - | <center><math>(+) \cdot (+) = (+)</math></center> | + | |
| - | <center><math>(-) \cdot (-) = (+)</math></center> | + | |
| - | <center><math>(+) \cdot (-) = (-)</math></center> | + | |
| - | <center><math>(-) \cdot (+) = (-)</math></center> | + | |
| - | }}{{p}} | + | |
| - | {{AI2|titulo=Actividad Interactiva: ''Regla de los signos''''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado=1. Practica el producto de números enteros. | + | |
| - | |actividad= | + | |
| - | Introduce el resultado con el teclado y pulsa "intro". | + | |
| - | Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/Multiplicar_1.html | + | |
| - | width=500 | + | |
| - | height=300 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| + | =Operaciones con números enteros= | ||
| + | {{Introducción operaciones con enteros}} | ||
| + | {{p}} | ||
| + | Las operaraciones con enteros son similares a las [[Números naturales: Operaciones | operaciones con naturales]], pero con las peculiaridades que aportan los números negativos. Veamos un video a modo de introducción. | ||
| - | ===División=== | + | {{Video_enlace_julioprofe |
| - | La división de números enteros, al igual que la [http://maralboran.ath.cx/wikipedia/index.php/N%C3%BAmeros_naturales#Divisi.C3.B3n división con números naturales], no siempre es otro entero. | + | |titulo1=Operaciones con enteros |
| - | Con la división , al igual que con la multiplicación, se aplica la misma regla de los signos. | + | |duracion=5'53" |
| - | + | |sinopsis=Breve resumen de las operaciones con enteros. | |
| - | {{AI2|titulo=Actividad Interactiva: ''División de números enteros''''|cuerpo= | + | |url1=https://www.youtube.com/watch?v=Sj9rThGLz9Q |
| - | {{ai_cuerpo | + | |
| - | |enunciado=1. Practica el cociente de números enteros. | + | |
| - | |actividad= | + | |
| - | Introduce el resultado con el teclado y pulsa "intro". | + | |
| - | Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. | + | |
| - | + | ||
| - | Aplicaremos la regla de lo signos al igual que con el producto: | + | |
| - | + | ||
| - | {{caja|contenido= | + | |
| - | <center><math>(+) : (+) = (+)\;\!</math></center> | + | |
| - | <center><math>(-) : (-) = (+)\;\!</math></center> | + | |
| - | <center><math>(+) : (-) = (-)\;\!</math></center> | + | |
| - | <center><math>(-) : (+) = (-)\;\!</math></center> | + | |
| - | }}{{p}} | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/1y2_eso/enterosdesp/dividir_1.html | + | |
| - | width=500 | + | |
| - | height=300 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | }} | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | + | ==Suma y resta de enteros== | |
| - | ===Potencias=== | + | ===Suma y resta de dos números enteros=== |
| - | Los enteros cumplen las mismas [http://maralboran.ath.cx/wikipedia/index.php/N%C3%BAmeros_naturales#Potenciaci.C3.B3n propiedades de las potencias de los naturales]. | + | {{Suma y resta de dos números enteros}} |
| - | {{Caja Amarilla|texto='''Potencia de un número negativo:'''<br> | + | {{p}} |
| - | Al elevar un número negativo a una potencia, el resultado es positivo si el exponente es par y negativo si es impar. | + | ===Suma y resta de más de dos números enteros=== |
| - | }}{{p}} | + | {{Suma y resta de más de dos números enteros}} |
| - | Por ejemplo:<math>(-2)^3=-8 \,\!</math> y <math>(-2)^4=16 \,\!</math>.{{p}} | + | |
| - | + | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Potencias de números enteros''''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado=1. Potencias de exponente negativo. | + | |
| - | |actividad= | + | |
| - | Se define la potencia de exponente negativo como: | + | |
| - | + | ||
| - | {{Caja|contenido=<math>a^{-n}= \cfrac {1}{a^n}</math>}} | + | |
| - | + | ||
| - | Calcula las siguientes potencias y comprueba los resultados en la escena siguiente: | + | |
| - | + | ||
| - | a) <math>3^{-5}</math>{{b}}b) <math>5^{-3}</math>{{b}}c) <math>7^{-2}</math>{{b}}d) <math>2^{-7}</math> | + | |
| - | + | ||
| - | {{Caja|contenido=<iframe> | + | |
| - | url=http://maralboran.ath.cx/web_ma/descartes/3_eso/Potencias/potencias31_1.html | + | |
| - | width=450 | + | |
| - | height=250 | + | |
| - | name=myframe | + | |
| - | </iframe>}} | + | |
| - | + | ||
| - | Introduce el resultado con el teclado y pulsa "intro". | + | |
| - | Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados. | + | |
| - | + | ||
| - | Si obtienes resultados un poco "extraños" prueba a aumentar el número de decimales del resultado en el control de la parte de arriba. | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| + | ===Propiedades de la suma y de la resta de números enteros=== | ||
| + | {{Propiedades de la suma y de la resta de números enteros}} | ||
| + | {{p}} | ||
| + | {{Multiplicación y cociente de números enteros}} | ||
| + | {{p}} | ||
| + | ==Potencias de números enteros== | ||
| + | {{Potencias enteros}} | ||
| + | {{p}} | ||
| + | ==Raíces cuadradas de números enteros== | ||
| + | La definición de raíz cuadrada de un número entero es la misma que la dada para números naturales. | ||
| - | ==Ejercicios y problemas== | + | Ver: [[Raíz cuadrada (1º ESO)|'''Raíz de un número natural''']] |
| - | ===Ejercicios=== | + | |
| - | {{ejercicio | + | |
| - | |titulo=Ejercicios | + | |
| - | |cuerpo= | + | |
| - | + | ||
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | '''1. '''Ordena los siguientes números enteros: -3, -16, 2, -7, 9, 0. | + | |
| - | |sol= | + | |
| - | <math>-16<-7<-3<0<2<9</math> | + | |
| - | }} | + | |
| - | {{ejercicio_cuerpo | + | {{Def raiz cuadrada}} |
| - | |enunciado= | + | |
| - | '''2. '''Calcula: | + | |
| - | :a) <math>|-13| \,\!</math>{{b}}b) <math>|(2-8)-4| \,\!</math>{{b}}c) <math>||3-5|-|2-11||\,\!</math> | + | |
| {{p}} | {{p}} | ||
| - | |sol= | + | ===Número de soluciones de una raíz cuadrada=== |
| - | a) 13{{b}}b) 10{{b}}c) 7 | + | {{Número de soluciones de una raíz cuadrada}} |
| - | }} | + | |
| - | + | ||
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | '''3. '''Calcula: | + | |
| - | :a) <math>16-(9-5)-5+2= \,\!</math> | + | |
| - | :b) <math>(-15-13)-9-(2-12+6)= \,\!</math> | + | |
| - | :c) <math>(-3) \cdot [5 \cdot (8-6) -3 \cdot (3-7)]=</math> | + | |
| {{p}} | {{p}} | ||
| - | |sol= | + | ===Raíces cuadradas con la calculadora=== |
| - | a) 9{{b}}b) -33{{b}}c) -66 | + | {{Raíces cuadradas con la calculadora}} |
| + | {{p}} | ||
| + | ===Raíces de otros índices (Ampliación)=== | ||
| + | {{AI_melide | ||
| + | |titulo1=Raíces de otros índices | ||
| + | |descripcion=Actividades sobre raíces de índice mayor que 2. | ||
| + | |url1=http://maralboran.org/web_ma/Melide/Potencias_y_raices/AMPLIACION_Raicesdeotrosindices.html | ||
| }} | }} | ||
| - | |||
| - | {{ejercicio_cuerpo | ||
| - | |enunciado= | ||
| - | '''4. '''Calcula: | ||
| - | :a) <math>(-2)^3 \,\!</math>{{b}}b) <math>-2^4 \,\!</math>{{b}}c) <math>(-2)^6 \,\!</math>{{b}}d) <math>(-1)^{10} \,\!</math>{{b}}e) <math>(-1)^{11}\,\!</math>{{b}}f) <math>-2^0 \,\!</math> | ||
| {{p}} | {{p}} | ||
| - | |sol= | + | ==Operaciones combinadas con números enteros== |
| - | a) -8{{b}}b) -16{{b}}c) 64{{b}}d) 1{{b}}e) -1{{b}}f) -1 | + | {{Jerarquía de las operaciones con números enteros}} |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| + | {{Ejemplos operaciones con enteros}} | ||
| + | {{p}} | ||
| + | ==Calculadora== | ||
| + | ===Suma, resta, multiplicación y división=== | ||
| + | {{Casio FX-100MS: Suma, resta, multiplicación y división}} | ||
| + | {{p}} | ||
| + | ===Opuesto=== | ||
| + | {{Casio FX-100MS: Opuesto}} | ||
| + | {{p}} | ||
| + | ===Paréntesis=== | ||
| + | {{Casio FX-100MS: Paréntesis}} | ||
| + | {{p}} | ||
| + | ===Potencias=== | ||
| + | {{Casio FX-100MS: Potencias}} | ||
| + | {{p}} | ||
| + | ==Ejercicios y problemas== | ||
| + | {{wolfram operaciones enteros}} | ||
| + | {{p}} | ||
| + | {{Problemas con enteros}} | ||
| - | ===Problemas=== | ||
| - | {{ejercicio | ||
| - | |titulo=Problemas | ||
| - | |cuerpo= | ||
| - | {{ejercicio_cuerpo | + | [[Categoría: Matemáticas]][[Categoría: Números]] |
| - | |enunciado= | + | |
| - | '''1. ''' Estamos en la planta 345 de un gran rascacielos del futuro y bajamos en ascensor a la planta -15. ¿Cuánto tiempo tardaremos si el ascensor tarda 1 segundo en bajar 5 pisos? | + | |
| - | |sol= | + | |
| - | 1' 12" | + | |
| - | }} | + | |
| - | + | ||
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | '''2.''' Pitágoras, filósofo y matemático griego, nació el año 582 a.C. ¿Cuántos años han pasado hasta el año 2007 d.C.? | + | |
| - | |sol= | + | |
| - | 2.589 años | + | |
| - | }} | + | |
| - | + | ||
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | '''3. '''Durante el ascenso a una montaña, la temperatura desciende 2 grados cada 200 m de ascenso. ¿A qué altura habrá que ascender para alcanzar -15ºC, si en el punto de partida, la temperatura es de 5ºC y este está a una altitud de 300 m? | + | |
| - | |sol= | + | |
| - | 2.300 m. | + | |
| - | }} | + | |
| - | }} | + | |
Revisión actual
| Enlaces internos | Para repasar | Enlaces externos |
| Indice | WIRIS Geogebra Calculadora |
Los números enteros
Estamos acostumbrados a utilizar números en multitud de ocasiones. Al levantarnos vemos la hora en el despertador, al calentar algo en la cocina puede que aparezca marcada la potencia con un entero, el precio de cualquier cosa que compremos está marcada con números, ...
En muchas situaciones utilizamos incluso valores negativos: "Pulsa el -1 para bajar al primer sótano", "¡Qué frío hace hoy! El termómetro marca 5º bajo cero (-5º)".
Los primeros en usar números negativos fueron los chinos, que utilizaban ábacos con varillas de distintos colores para diferenciar los positivos de los negativos. En Europa, sin embargo, fue más difícil su aceptación y grandes matemáticos como Descartes o Cardano se referían a los negativos como "números falsos". A partir del siglo XVIII y gracias al trabajo, entre otros, de Euler, su uso se universalizó y se convirtieron en parte esencial de las matemáticas.
- Introducción histórica de los números negativos.
- SOS, Estoy en números rojos.
- Cuadrados mágicos.
Números naturales
Empezaremos recordando primero qué eran los números naturales.
El conjunto de los números naturales es:
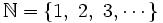
Se trata de un conjunto con infinitos elementos y sirven para:
- Contar (números cardinales: 1, 2, 3, ...).
- Ordenar (números ordinales: 1º, 2º, 3º, ...).
- Identificar y diferenciar los distintos elementos de un conjunto.
Puesto que los números naturales se utilizan para contar elementos, el cero (0) puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de las matemáticas, el conjunto de los números naturales puede incluir o no al cero.
Veamos distintos ejemplos de uso de los números naturales:
- Como número cardinal: Los días de la semana son 7.
- Como número ordinal: El atleta británico quedó 3º en la prueba de cien metros lisos.
- Como identificador: Tú número de carnet de socio del Atleti es el 2868.
El conjunto de los números naturales: origen y definición.
El conjunto de los números naturales: origen y definición.
Tutorial de introducción al tema:
- Números naturales.
- Sistemas de numeración.
- Sistema de numeración decimal.
Hace unas horas tenía 16 años y el año que viene cumpliré 19. ¿Cómo explicas esta situación?
Ejercicios de autoevaluación sobre números naturales.
Existen dos teorías sobre el origen de la numeración, que además está relacionada con la cuestión de qué números aparecieron primero, los cardinales (1, 2, 3,...) o los ordinales (1º, 2º, 3º,...) La teoría que genera más consenso defiende el argumento de la necesidad. Todo habría comenzado a causa de la necesidad de contar objetos; por ello se habrían creado primero los números cardinales y después, los ordinales.
La otra teoría defiende la base espiritual de los números, que habrían tenido un uso ritual: cierto tipo de ceremonias requerían que los participantes se desplazaran o se situaran en un orden ritual preestablecido; por eso los números ordinales serían anteriores a los cardinales. Esta teoría además postula que los números se originaron en un lugar geográfico determinado, desde el que se propagaron al resto del mundo; también establece la división de los números naturales en pares e impares, considerando los impares masculinos y los pares, femeninos, una clasificación que comparten hoy en día muchas culturas del planeta.
(Extracto de "El mundo es matemático: Del ábaco a la revolución industrial". Pág. 10)"
Véanse los artículos de la BBC:
- ¿Sabes que el 1 y el 2 no son del mismo género y que los números tienen personalidades?
- Lo que quizás no sabías de los números
Representación de los números naturales
Podemos representarlos en una recta:
Los números que nos sirven para contar, los números naturales, uno de los más viejos inventos de la Humanidad. ¿Cómo serían nuestras vidas sin la existencia de estos números?... Desde los pitagóricos, que los consideraron como el principio y la explicación de todo el Universo, hasta nuestros días estos números han ejercido un poderoso influjo sobre los matemáticos de todas las épocas. Uno de los campos que ha tenido en jaque a los grandes matemáticos es el de los números primos; una auténtica caja de sorpresas. Aún hoy, utilizando potentes ordenadores, no se han podido demostrar algunas de las conjeturas formuladas sobre estos números hace más de doscientos años. Veremos algunas de ellas y descubriremos una de las aplicaciones más extrañas de los números primos en la actualidad, su utilización en criptografía. (Ver resumen detallado)
Para más información: Números naturales
Números negativos y positivos
- Los números negativos son los números menores que cero. Para representarlos se les pone un signo menos (-) delante:
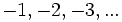
- Los números positivos, son los mayores que cero. Pueden ir precedidos de un signo más (+), pero es habitual no ponerlo:
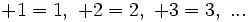
Reglas:
- Los números negativos se escriben precedidos del signo menos (-).
- Si un número lleva signo + o no lleva signo entenderemos que es positivo.
- En las operaciones, los números negativos se escriben entre paréntesis cuando queremos evitar que aparezcan dos símbolos de operación seguidos.
Los números enteros pueden tener signo + (positivos) o signo - (negativos). En este video veremos cuando son necesarios los signos y cuando no. También veremos como se representan en la recta numérica.
Utilidad de los números negativos y positivos
Los números positivos nos sirven para expresar muchas situaciones de la vida cotidiana. Sin embargo, no siempre nos sirven para representar situaciones contrarias que requieren del uso de números negativos, como un saldo deudor en una cuenta bancaria, una temperatura bajo cero, el número de una planta del sótano de un edificio, etc.
Interpretar números negativos. Los números negativos y positivos, además de servir para representar cantidades fijas, también se pueden utilizar para expresar variaciones que sufre una magnitud. Ejemplo: Expresa numéricamente cada enunciado:
Solución: Solución:
|
Utilidad de los números negativos en la vida real.
Números enteros
Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor hay que restarle uno mayor. Nos vemos obligados a ampliar el concepto de números naturales, introduciendo un nuevo conjunto numérico llamado números enteros.
El conjunto de los números enteros
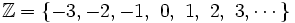
Está formado por:
- El conjunto de los números naturales o enteros positivos :
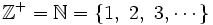 .
.
- Sus opuestos, los enteros negativos:
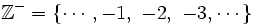 .
.
- El cero (0).
Como consecuencia, 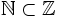 , que se lee: "el conjunto de los números naturales está incluido en el conjunto de los números enteros".
, que se lee: "el conjunto de los números naturales está incluido en el conjunto de los números enteros".
Los números enteros: utilidad y definición.
Los números enteros: utilidad y definición.
En este video vamos a ver lo que son los números enteros y también las clases de números enteros que hay, es decir, números enteros positivos y números enteros negativos, además del cero.
El conjunto de los números enteros. El subconjunto de los números enteros positivos, el de los negativos y el cero. Representación y notación.
El conjunto de los números enteros. Utilidad. Representación y operaciones en la recta numérica.
Las criaturas o entes llamados números no exixten realmente: nadie ha visto jamás un número, ya sea famoso (como el representado por el símolo 5 y llamado cinco) o no. Los números sólo exixten a la luz de la inteligencia humana. Existen en la medida en que nos son útiles. Los Números Naturales son todos enteros y positivos. Son muy útiles para contar, pero tienen sus limitaciones, de manera que hubo que inventar otro tipo de números...
Number systems evolved from the natural "counting" numbers, to whole numbers (with the addition of zero), to integers (with the addition of negative numbers), and beyond. These number systems are easily understood using the number line.
(Disponibles los subtítulos en inglés)
Utilidad de números negativos en la vida real. El conjunto de los números enteros. Representación en la recta numérica.
Los números enteros son infinitos y, al igual que los números naturales sirven para contar. Sin embargo, los números enteros permiten expresar cantidades negativas como un saldo deudor en una cuenta bancaria, un año de la era antes de Cristo, el número de una planta del sótano de un edificio, etc.
Actividad sobre números enteros.
El termómetro y los números enteros.
Actividades sobre números enteros.
Representación de los números enteros
Representación de los números enteros
Los números enteros podemos representarlos en una recta:
- Sobre ella marcamos el número cero.
- A la derecha del cero, y a distancias iguales, se van señalando los números positivos: 1, 2, 3, ...
- A la izquierda del cero, y a distancias iguales que las anteriores, se van señalando los números negativos: −1, −2, −3, ...
- Escena en la que vas a conocer como se representan los números enteros en la recta numérica.
- Actividad en la que debes averiguar el número entero que se corresponde con un punto dado de la recta numérica.
Los números negativos en la recta numérica.
En este video vamos a ver como se representan gráficamente los números enteros sobre la recta numérica y algunos ejemplos.
Introducción a los números negativos. Representación en la recta numérica.
Representa en la recta numérica -4 y 7, e indica cuántos números enteros hay entre ellos.
|
Actividad: Números enteros. Representación
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Valor absoluto de un entero
El valor absoluto de un número entero  se representa por
se representa por 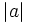 y se define de la siguiente manera:
y se define de la siguiente manera:
- Si el número es positivo, su valor absoluto es él mismo.
- Si el número es negativo, su valor absoluto es igual a su opuesto.
Propiedades
- El valor absoluto de un número es la distancia que lo separa del cero en la recta numérica.
- El valor absoluto de un número siempre es positivo o cero.
- El valor absoluto de cero es cero.
Valor absoluto de un número entero. Interpretación métrica.
- Representación de los números enteros en la recta real.
- Valor absoluto de un número entero. Interpretación métrica.
Valor absoluto de un número entero. Ejemplos.
Valor absoluto de un número entero. Ejemplos.
Valor absoluto de un número entero. Ejemplos.
En este video vamos a ver lo que es el valor absoluto de un número entero y también vamos a aprender a calcularlo.
Valor absoluto de un entero.
Valor absoluto como distancia entre números.
Halla 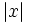 , cuando
, cuando 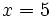 ,
, 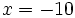 y
y 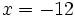 .
.
Compara:
- a)
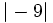 y
y 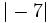
- b)
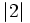 y
y 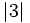
- c)
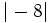 y
y 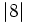
- d)
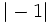 y
y 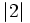 .
.
Ordena de menor a mayor: 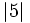 ,
, 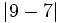 ,
, 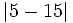 ,
, 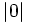 y
y 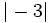 .
.
- Actividad en la que puedes obtener el valor absoluto de un número entero.
- Actividad en la que deberás obtener el valor absoluto de un número entero.
Aprende a pensar el valor absoluto como la distancia a cero, y practica encontrar valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Halla el valor absoluto.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Compara valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Cálculo de distancias mediante valores absolutos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Opuesto de un entero
El opuesto de un número entero,  , es otro número entero,
, es otro número entero, 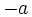 , simétrico de
, simétrico de  respecto del cero. En consecuencia, se encuentra a la misma distancia del cero que
respecto del cero. En consecuencia, se encuentra a la misma distancia del cero que  , pero tiene signo contrario. Lo escribiremos
, pero tiene signo contrario. Lo escribiremos 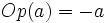 .
.
Es obvio que si 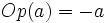 entonces
entonces 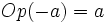 , y viceversa. Por eso, también se dice que
, y viceversa. Por eso, también se dice que  y
y 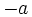 son números opuestos.
son números opuestos.
Concepto de opuesto de un número entero. Ejemplos.
Concepto de opuesto de un número entero. Ejemplos.
Opuesto de un número entero. Representación en la recta numérica.
Uso del signo "menos" para la obtención del opuesto de un número entero.
Ejercicios sobre números opuestos.
- Actividad en la que podrás ver la relación entre un número y su opuesto mediante su representación en la recta real.
- Actividad en la que deberás obtener el opuesto de un número entero.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
Números opuestos.
Aviso: Alguna pregunta puede ser de números que no son enteros.
|
Actividad: Opuesto de un número entero
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Orden en el conjunto de los enteros
En la representación de los números enteros en la recta numérica se observa el orden que existe en dicho conjunto.
Un número es mayor que otro si está situado más a la derecha en la recta numérica y es menor si está situado más a la izquierda.
Relación de orden
Dados dos números,  y
y  , se dará uno de los siguientes casos:
, se dará uno de los siguientes casos:
- El primero es menor que el segundo:
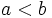 (Se lee "a es menor que b").
(Se lee "a es menor que b").
- El primero es igual que el segundo:
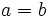 (Se lee "a es igual que b").
(Se lee "a es igual que b").
- El primero es mayor que el segundo:
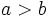 (Se lee "a es mayor que b").
(Se lee "a es mayor que b").
Al comparar números, además de los símbolos anteriores, podemos utilizar también los siguientes:
- Menor o igual que (
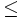 )
)
- Mayor o igual que (
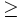 )
)
- Distinto (
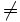 )
)
Propiedades
- Todo número negativo es menor que cero y todo número positivo es mayor que cero.
- Si dos números son positivos, el mayor es el que tiene mayor valor absoluto.
- Si dos números son negativos, el mayor es el que tiene menor valor absoluto.
- Si
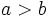 , entonces
, entonces 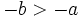
Representación y ordenación de números enteros.
Hacer una comparación de números enteros significa conocer cuál de esos números es mayor (o menor que el otro). Una forma de saberlo es haciendo la representación gráfica de esos números enteros sobre la recta. Los números situados más hacia la derecha en la recta siempre son mayores que los situados a su izquierda.
Ordenando números negativos.
Comprueba gráficamente que 5 > -5.
Comprueba gráficamente que -6 > -1.
Escribe y representa todos los números enteros más grandes que -1 y más pequeños que +5.
Escribe y representa en la recta numérica todos los números comprendidos entre -5 y 1.
Escribe y representa en la recta numérica todos los números enteros más grandes que -3 y más pequeños que 3.
Escribe un valor correcto para x e y que cumplan x < 8 < y.
Ordena de menor a mayor: 5, -3, 0, 4, -6, +1, -1, 3, -7, +6
En una estación meteorológica al sur de Argentina se realizó una medición de la temperatura en el transcurso del día, obteniendo los siguientes resultados: -10º, -3º, 12º, 1º, -8º, -5º, 4º. Ordénalos.
- Actividad en la que puedes ver como se ordenan dos números enteros comparando su posición en la recta numérica.
- Actividad para ordenar dos números enteros.
- Actividad para ordenar varios números enteros.
Ordenar números enteros.
Ordenar números enteros.
Ejercicios de autoevaluación sobre el orden en el conjunto de los números enteros.
|
Actividad: Orden en el conjunto de los números enteros
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Actividades
Repaso del tema de números enteros.
Ejercicios de autoevaluación sobre números enteros.
Actividad en la que podrás comprobar tus conocimientos sobre números enteros.
Ejercicios de autoevaluación sobre números enteros y valor absoluto.
Actividad en la que podrás comprobar tus conocimientos sobre el opuesto y el valor absoluto de un número.
Operaciones con números enteros
Un toque divertido para empezar el tema:
Troncho no quiere saber nada de números naturales, ni enteros, ni como se opera con ellos.
Puedes encontrar ejercicios sobre este vídeo y material similar en: http://www.angelitoons.com/
Las operaraciones con enteros son similares a las operaciones con naturales, pero con las peculiaridades que aportan los números negativos. Veamos un video a modo de introducción.
Breve resumen de las operaciones con enteros.
Suma y resta de enteros
Suma y resta de dos números enteros
Sabemos que los números enteros pueden tener signo positivo (un más o nada delante del número) o signo negativo (un menos delante del número). Sin embargo, cuando dos enteros aparecen juntos, sus signos expresan una operación.
- Suma: Siempre que vemos dos enteros juntos, sin más separación entre ellos que sus signos, lo que tenemos delante es una suma. Para realizar esa suma puedes guiarte por la lógica: los números negativos representan pérdidas, los positivos ganancias y el resultado de la operación es el balance entre ganancias y pérdidas.
- Resta: La resta de números enteros es el resultado de sumar el primero con el opuesto del segundo.
Por ejemplo, si vemos escrito:
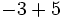
sabemos que uno es negativo y el otro es positivo, pero al mismo tiempo estamos indicando una cuenta. Algo así como "perdemos 3, pero ganamos 5". Lógicamente, el resultado es que "ganamos 2", es decir:
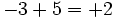
Lo que realmente sucede es que estamos haciendo una suma de número enteros, pero omitimos el símbolo de la operación, por economía del lenguaje. En realidad deberíamos escribir:
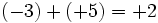
Siguiendo esa lógica de balance entre pérdidas y ganancias, para sumar números enteros seguiremos las siguientes reglas:
Procedimiento: Suma de números enteros
Dependiendo del signo de los dos números a sumar, tenemos que:
- Si tienen el mismo signo, se suman los valores absolutos y se pone el mismo signo que tenían los números.
- Si tienen distinto signo, se restan los valores absolutos (el mayor valor absoluto menos el menor) y se pone el signo del que tenga mayor valor absoluto.
- a)
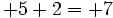
- b)
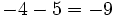
- c)
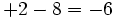
- d)
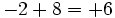
¿Qué pasa en cada situación?
- En el primero los dos son positivos (ganancias) y el resultado es la suma de esas ganancias.
- En el segundo los dos son negativos (pérdidas) y el resultado es la suma de esas pérdidas.
- En el tercero tienen signos distintos, pero las pérdidas son mayores que las ganancias, así que el resultado es negativo.
- En el cuarto tienen signos distintos, pero las ganancias son mayores que las pérdidas, así que el resultado es positivo.
Tutorial que usa el símil de las batallas entre soldados para explicar la suma de números enteros, según tengan o no el mismo signo.
Ejemplo sobre lo explicado en el tutorial anterior.
El mismo ejemplo del tutorial 1b por otro método (agrupando primero los del mismo signo).
Un error frecuente.
Ejemplos de como se suman números enteros, según tengan o no el mismo signo.
Ejemplos de como se suman números enteros, según tengan o no el mismo signo, usando la recta numérica.
Suma de números enteros.
Resta de números enteros.
Suma de números enteros.
Resta de números enteros.
Interpretación geométrica de la suma de números enteros.
Suma y resta de números enteros.
Calcula:
a) 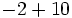 b)
b) 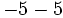 c)
c) 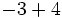 d)
d)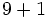
e) 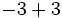 f)
f) 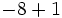 g)
g) 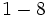 h)
h) 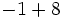 i)
i) 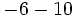
- Actividad en la que se te plantean problemas para practicar la suma y resta de dos números enteros.
- Actividad para calcular la suma o resta de dos números enteros.
Suma y resta de dos números enteros.
Suma y resta de dos números enteros.
Suma de dos números enteros.
Suma y resta de más de dos números enteros
Cuando sumemos más de dos números enteros podemos proceder de dos formas:
- Método 1: Sumar los positivos por un lado y los negativos por otro y, después, efectuar la resta de los resultados.
- Método 2: Ir sumando o restando paso a paso, de izquierda a derecha.
Ejemplos de como se suman más de dos números enteros por los 2 métodos antes descritos.
Ejemplos de como se suman números enteros, según tengan o no el mismo signo, usando la recta numérica.
Calcula:
a) 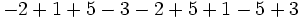
b) 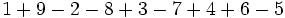
Calcula:
a) 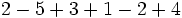
b) 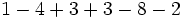
c) 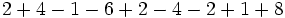
- Actividad en la que se te plantean problemas para practicar la suma y resta de tres números enteros por dos métodos.
- Actividad para calcular la suma o resta de tres números enteros.
Actividad para calcular la suma de más de tres números enteros.
Actividad para calcular la suma de más de tres números enteros.
Propiedades de la suma y de la resta de números enteros
Propiedades de la suma
- Operación interna: el resultado de sumar dos números enteros es otro número entero.
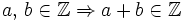
- Propiedad conmutativa: La suma no varía al cambiar el orden de los sumandos.
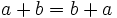
- Propiedad asociativa: El resultado de la suma es independiente de la forma en que se agrupen los sumandos.
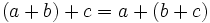
- Elemento neutro: El elemento neutro para la suma es el 0.
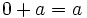
- Elemento opuesto: Todo número entero,
 , tiene un opuesto,
, tiene un opuesto, 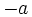 , que al sumarse con él da el elemento neutro.
, que al sumarse con él da el elemento neutro.
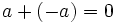
Conmutativa:
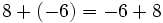
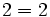
Asociativa:

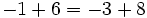
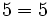
Elemento neutro:
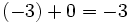
Elemento opuesto:
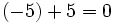
Esto es, el opuesto de 5 es -5 y el opuesto de -5 es 5. Por tanto, decimos que 5 y -5 son opuestos.
Propiedades de la suma de números enteros. Ejemplos (1ª parte)
1) Calcula:
- a) (-5)+(+7)
- b) (+3)+(-2)
- c) (-2)+(+4)+(+3)
- d) (-7)+(-5)+(-1)
- e) (-3)+(-9)+(-6)
2) Completa la tabla: (Ejercicio sobre el opuesto de un número entero)
3) Completa:
- a) (-7)+ ... = 0
- b) (+4)+ ... = 0
- c) ... +(-5) = 0
- d) ... +(+3) = 0
4) Transforma las restas en sumas y después calcula:
- a) (+5)-(-3) =
- b) (+4)-(+2) =
- c) (+8)-(-8) =
5) Calcula:
- a) (-6)-(+3) =
- b) (+3)-(-6) =
Observando esto, ¿tiene la resta la propiedad conmutativa?
1) Calcula:
- a) (+5)-[(+4)-(-5)]=
- b) [(+5)-(+4)]-(-2)=
Observando esto, ¿tiene la resta la propiedad asociativa?
2) Calcula:
- a) Op[(+5)+(+3)]=
- b) Op[(-4)+(-2)]=
- c) Op[(-5)+(-2)]=
- d) Op[Op(-5)]=
3) Calcula Op[(-5)-(+2)].
4) Contesta:
- a) ¿Cuál es el opuesto del opuesto de -3?
- b) ¿Y el opuesto del opuesto de +5?
1) Calcula:
- a) (+7)+(-3)+(-4)=
- b) (+5)+(-4)+(-2)=
- c) (-3)+(-5)+(-4)=
- d) (-7)+(-10)+(-3)=
2) Calcula:
- a) (-5)-(-8)=
- b) (-20)-(-40)=
- c) (+55)-(-25)=
- d) (-35)-(-55)=
3) Calcula:
- a) -(-3)=
- b) -(-5)=
- c) -(-20)=
- d) -(-17)=
4) ¿Qué propiedades de la suma se dan en las siguientes igualdades?
- a) (+5)+(-3) = (-3)+(+5)
- b) (-7)+0- = -7
- c) [(+1)+(-4)]+(+2) = (+1)+[(-4)+(+2)]
- d) (+15)+(-15) = 0
5) Contesta:
- a) ¿Cuál es el elemento neutro de la suma de números enteros? ¿Por qué?
- b) Calcula el opuesto del opuesto de 3. ¿Cuál es el opuesto del opuesto de un número entero?
- c) ¿Puede ser la diferencia de dos números enteros negativos un número entero positivo? Pon ejemplos.
- d) ¿Cuál es la suma de dos números opuestos?
- e) ¿Tiene la resta de números enteros la propiedad conmutativa? Pon un ejemplo.
- f) ¿Qué propiedad de la suma de números enteros no la tiene la suma de números naturales?
- g) ¿En qué parte de la recta están situados los opuestos de los números enteros positivos?
Propiedades de la resta
- Operación interna: el resultado de restar dos números enteros es otro número entero.
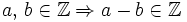
- Propiedad conmutativa: No se cumple
- Propiedad asociativa: No se cumple
Multiplicación o producto de números enteros
Regla de los signos para el producto
- Si dos números enteros tienen el mismo signo su producto es un entero positivo.
- Si dos números enteros tienen distinto signo, el producto es un entero negativo.
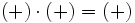 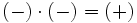 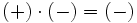 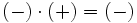 |
- Los paréntesis aparecen para separar los símbolos · y : de los símbolos + y -.
- Si el primer número es negativo no hace falta poner paréntesis.
- Cuando el signo (positivo) del segundo número no aparece escrito los paréntesis no son necesarios.
- a)
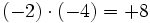
- b)
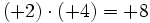
- c)

- d)
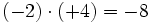
Aunque las expresiones anteriores son correctas, si nos atenemos a las reglas anteriores, los ejemplos b), c) y d) se podrían haber escrito de la siguiente manera más simple:
- b)
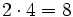
- c)
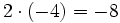
- d)
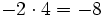
Producto de números enteros. Regla de los signos. Ejemplos
Producto de números enteros.
Aprende a usar la regla de los signos para multiplicar números enteros.
When number systems were expanded to include negative numbers, rules had to be formulated so that multiplication would be consistent regardless of the sign of the operands.
(Disponibles los subtítulos en inglés)
Opera:
- Actividad en la que se plantean problemas para aprender a multiplicar números enteros.
- Actividad para practicar la multiplicación de números enteros.
Practica el producto de números enteros
En esta escena podrás practicar la multiplicación de números enteros.
Si tienes problemas con la actividad a la hora de escribir las soluciones en los recuadros, haz lo siguiente:
- Haz click con el ratón en el cuadro donde va la repuesta.
- Pulsa "Enter".
- Te aparecerá el cursor y ya podrás escribir la solución.
Ejercicios de autoevaluación sobre multiplicaciones de números enteros.
Propiedades del producto de números enteros
Propiedades de la multiplicación
- Operación interna: El producto de dos números enteros es otro número entero:
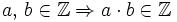
- Propiedad conmutativa: El producto no varía al cambiar el orden de los factores.
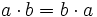
- Propiedad asociativa: El resultado de una multiplicación es independiente de la forma en que se agrupen los factores.
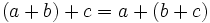
- Propiedad distributiva: El producto de un número por una suma (o resta) es igual a la suma (o resta) de los productos del número por cada sumando.

- Elemento neutro: El elemento neutro para la multiplicación es el 1.
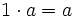
Gracias a la propiedad distributiva, tenemos dos opciones a la hora de enfrentarnos a unos paréntesis:
- Podemos realizar primero las operaciones que aparezcan dentro de los paréntesis.
- Podemos aplicar la propiedad distributiva y eliminar los paréntesis sin completar las operaciones que aparezcan dentro de ellos.
Esta propiedad es clave para realizar operaciones combinadas que veremos proximamente.
La propiedad distributiva tiene una especie de propiedad "recíproca" que llamaremos sacar factor comun. En realidad es la misma propiedad, pero usada "al revés". La idea es buscar un divisor común a todos los sumandos que tengamos y "sacarlo" fuera del paréntesis en el que meteremos al resultado de dividir a cada uno de los sumandos por ese factor.
- a) En este primer ejemplo sacaremos 3 como factor común:
- b) En este otro sacaremos 5 como factor común:
Sacar factor común no nos será especialmente útil en este tema, sin embargo, si será de gran utilidad, más adelante, cuando trabajemos con expresiones algebraicas.
- Propiedades del producto de números enteros. Ejemplos.
- Ejercicios:
1) Calcula:
- a)
![[(-4) \cdot (-2)] \cdot 6\;](/wikipedia/images/math/4/4/a/44a47677fd91afc7f8ed6c96632ec942.png)
- b)
![(-4) \cdot [(-2)] \cdot 6]\;](/wikipedia/images/math/b/1/9/b1976f580931741859d782c6d3346a15.png)
- c)
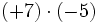
- d)
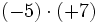
1) Calcula:
- a)
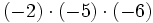
- b)
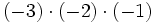
- c)
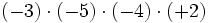
- d)
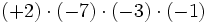
2) Calcula:
- a)
![[(-7) + (-3)] \cdot (+2)\;](/wikipedia/images/math/3/4/5/345ca286da82e44f4d7417853d6141b5.png)
- b)
![[(+4) - (+5)] \cdot (-3)\;](/wikipedia/images/math/6/d/6/6d6c19c9fa1c521567b33701a91f3a7c.png)
- c)
![(-5) \cdot [(+9) - (-5)]\;](/wikipedia/images/math/c/3/e/c3edcc45ed3f7456bfa1673b3a0d4f8a.png)
- d)
![(+2) \cdot [(+5) + (-2)]\;](/wikipedia/images/math/2/8/5/2856468702b11cb88edb046851bd6089.png)
3) Saca factor común:
- a)
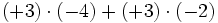
- b)
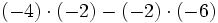
- c)
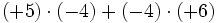
- d)
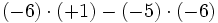
4) Sabiendo que a=-2, b=-3 y c=-1, calcula:
- a)
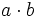
- b)

- c)
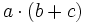
- d)
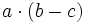
5) Completa la tabla (Ejercicios con operaciones y valor absoluto de números enteros)
6) Saca factor común descomponiendo previamente en producto de factores:
- a)
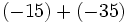
- b)
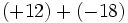
- c)
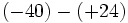
- d)
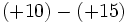
Ejercicios de autoevaluación sobre la propiedad distributiva del producto de enteros.
Ejercicios de autoevaluación sobre sacar factor común.
División o cociente de números enteros
Regla de los signos para el cociente
Con la división , al igual que con la multiplicación, se aplica la misma regla de los signos:
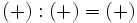 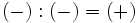 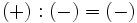 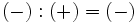 |
División o cociente de números enteros. Ejemplos.
División o cociente de números enteros. Ejemplos.
Cociente de números enteros.
- Actividad para aprender a dividir números enteros.
- Actividad para practicar la división de números enteros.
Practica el cociente de números enteros.
Ejercicios de autoevaluación sobre divisiónes de números enteros.
Propiedades de la división de números enteros
Propiedades de la división de números enteros
- La división de de números enteros no siempre es un número entero.
- La división de números enteros no tiene las mismas propiedades que producto. No tiene la propiedad conmutativa, ni la asociativa, ni la distributiva.
Al no tener la división de números enteros la propiedad asociativa, si aparecen varias divisiones consecutivas, sin paréntesis, tienen que hacerse de izquierda a derecha.
Fíjate en las siguientes operaciones:
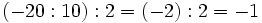
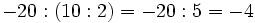
Por tanto, la división no es asociativa, así que si nos encontramos una cuenta como la de este ejemplo, pero sin paréntesis, tendremos que hacer las divisiones de izquierda a derecha, sin alterar el orden.
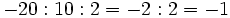
Ejercicios de autoevaluación sobre las propiedades del producto y cociente de números enteros.
Actividades y videotutoriales
Multiplicación y división de enteros. Regla de los signos.
Tutorial en el que se explica a través de varios ejemplos la multiplicación y división de números enteros, desde el caso en el que sólo intervienen dos números hasta cuando intervienen más.
- 00:00 a 06:38: Multiplicación y División simple de número enteros. (00:38 : Regla de los Signos.)
- 06:38 a 07:33: Ejercicios de Multiplicación y División simple.
- 07:33 a 12:30: Multiplicación y División compuesta de números enteros.
- 12:30 a 17:34: Ejercicios de Multiplicación y División compuesta.
Calcula:
Ejercicios sencillos de multiplicación y división de enteros.
Multiplicación y división:
Multiplicación y división de números enteros.
Introduce el resultado y cuando termines pulsa el botón "Corregir" de la parte inferior de la escena. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Ejercicios de autoevaluación sobre producto y cociente de números enteros.
En esta escena podrás practicar la multiplicación y división de números enteros.
Ejercicios de autoevaluación sobre multiplicaciones y divisiones de números enteros.
Ejercicios de autoevaluación sobre las propiedades del producto y del cociente de números enteros.
Suma, resta, multiplicación y división:
En esta escena podrás practicar la suma, resta, multiplicación y división de números enteros.
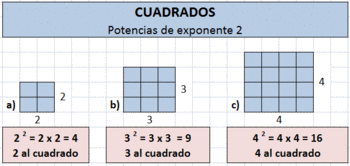
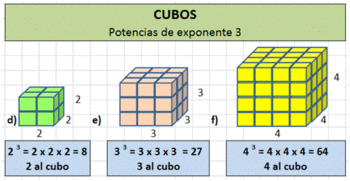
Potencias de números enteros
Los siguientes videotutoriales condensan lo que vamos a ver en este apartado sobre potencias de números enteros:
Cálculo de potencias cuya base es un número entero. Ejemplos.
Ejemplos de potencias de números enteros.
Tutorial en el que se explica a través de varios ejemplos la potencia con números enteros y las operaciones combinadas con multiplicación, división y potencia de números enteros.
- 00:00 a 05:55: Potencia de número enteros, definición.
- 05:55 a 09:15: Ejercicios simples de Potencias.
- 09:15 a 13:07: Ejercicios de Combinadas de Multiplicación, División y Potencias.
Potencias de números enteros.
Potencias de base entera y exponente natural. Producto de potencias. División de potencias. Potencias de una potencia. Potencia de un producto. Signo de una potencia.
Definición de potencia
La definición de potencia de exponente entero es la misma que la de números naturales.
Ver: Potencias de números naturales
Una potencia es un modo abreviado de escribir un producto de un número por sí mismo:
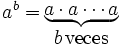 (Se lee: "
(Se lee: " elevado a
elevado a  ")
")- El número
 se llama base. Es el número que se multiplica por sí mismo.
se llama base. Es el número que se multiplica por sí mismo.
- El número
 se llama exponente. Es el número que indica las veces que la base aparece como factor.
se llama exponente. Es el número que indica las veces que la base aparece como factor.
- Por convenio, se establece que:
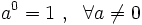 .
.
- Cuando el exponente de una potencia es el número 1 no se pone exponente, basta con poner el número de la base.
Cómo se leen las potencias:
Cuando el exponente es 2 se dice "elevado al cuadrado", cuando el exponente es 3 se dice "elevado al cubo". En los demás casos se dice "elevado a la cuarta, quinta, sexta... potencia".
Actividad para aprender a calcular potencias de números enteros.
Actividades sobre potencias de números enteros.
Signo de la potencia
Signo de la potencia
Dependiendo del signo de la base tenemos dos posibilidades:
- Base positiva: Al elevar un número positivo a una potencia, el resultado es positivo.
- Base negativa: Al elevar un número negativo a una potencia, el resultado es positivo si el exponente es par y negativo si es impar.
Cálculo de potencias cuya base es un número entero negativo. Ejemplos.
1) Completa la tabla. En ella debes indicar la base, el exponente, el valor y la cómo se leen las siguientes potencias de números enteros:
2) Escribe en forma de potencia:
- a)
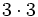
- b)
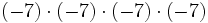
- c)
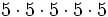
- d)
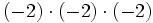
3) Escribe cómo se leen las siguientes potencias:
4) Escribe las siguientes potencias en forma de producto:
5) Escribe cada producto en forma de potencia, calcula su valor e indica cuál es la base y el exponente.
6) Calcula:
- a) Doce elevado al cuadrado.
- b) Once elevado al cubo.
- c) Tres elevado a la quinta.
- d) Dos elevado a la cuarta.
7) Desarrolla las siguientes potencias:
8) Calcula las siguientes potencias y razona cuánto valen todas las potencias de base 1:
- Actividad para aprender a calcular potencias de números enteros con base positiva o negativa.
- Actividad para practicar las potencias de enteros.
Calcula las siguientes potencias y comprueba los resultados en la escena siguiente:
a) ( − 3)4 b) ( − 4)5 c) ( − 10)5 d) ( − 2)10
Usa los pulsadores o el teclado para modificar los valores de la base y del exponente. Pulsa INICIO cada vez que quieras iniciar uno nuevo. Anota en tu cuaderno los resultados.
Actividad sobre potencias cuya base es un número entero.
Ejercicios de autoevaluación en los que debes determinar el signo de la potencia cuya base es un número entero.
Ejercicios de autoevaluación de potencias cuya base es un número entero.
Ejercicios de autoevaluación de potencias cuya base es un número entero.
Ejercicios de autoevaluación de potencias cuya base es un número entero.
Propiedades de las potencias de enteros
Las potencias de números enteros cumplen las mismas propiedades que las potencias de números naturales.
Ver: Propiedades de las potencias de números naturales
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
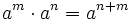
- 2. Cociente de potencias de la misma base:
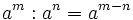
- 3. Potencia de un producto:
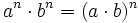
- 4. Potencia de un cociente:
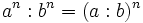
- 5. Potencia de otra potencia:
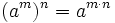
Propiedades de las potencias y ejemplos:
- Potencias de exponente 0.
- Potencias de exponente 1.
- Producto de potencias de la misma base.
- Cociente de potencias de la misma base.
Propiedades de las potencias y ejemplos:
- Potencia de otra potencia.
- Potencia de un producto.
- Potencia de un cociente.
Calcula:
- a)
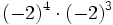 ; b)
; b) 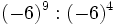
- c)
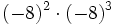 ; d)
; d) 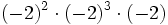
- e)
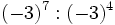 ; f)
; f) 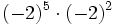
- g)
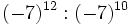 ; h)
; h) 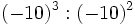
10) Escribe en forma de una sola potencia:
- a)
![[(-2)^3]^5\;](/wikipedia/images/math/8/8/6/886e30889b011f5f83334ec9296c0152.png) ; b)
; b) ![[(-3)^2]^3\;](/wikipedia/images/math/f/0/3/f037bb097909faad6873a0992df599fe.png)
- c)
![[(-5)^2]^4\;](/wikipedia/images/math/5/0/8/508d047dc4eb1a22b590a2f901a2fab9.png) ; d)
; d) ![[(-6)^3]^3\;](/wikipedia/images/math/4/c/8/4c8eef59c8fa17ac5bf2860de4ab42b4.png)
- e)
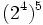 ; f)
; f) 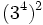
- g)
![[(-2)^1]^6\;](/wikipedia/images/math/d/f/3/df39089d6f5cc9c51e1d93713bb5f895.png) ; h)
; h) ![[(-2)^2]^6\;](/wikipedia/images/math/2/d/9/2d9edbe794a96dc0e0737db47be9067b.png)
- i)
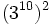 ; j)
; j) 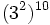
11) Expresa en forma de producto de varias potencias:
- a)
![[(-3) \cdot (-2) \cdot (-5)]^4\;](/wikipedia/images/math/3/2/6/3267df8521104f4db4a75cebb28001f7.png)
- b)
![[(-2) \cdot 5 \cdot (-6)]^2\;](/wikipedia/images/math/6/3/e/63e0b632e8c81875b6431d372a903f72.png)
- c)
![[2 \cdot 7 \cdot 6]^3\;](/wikipedia/images/math/1/a/0/1a083a19f18fa30e36b04f11289e2a1c.png)
- a)
![[(-2) \cdot (-3) \cdot (-6)]^3\;](/wikipedia/images/math/2/2/2/222cfc62f8027cac612dad7e3962dd04.png)
11) Expresa en forma de una sola potencia:
- a)
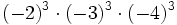
- b)
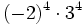
- c)
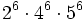
- d)
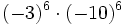
12) Calcula los cuadrados de los cinco primeros números positivos.
14) Escribe las cuartas potencias de: -3, -2, -5, 3, 2 y 5.
15) Calcula:
- a)
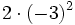 ; b)
; b) 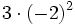
- c)
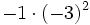 ; d)
; d) 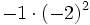
- e)
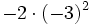 ; f)
; f) 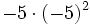
- g)
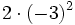
16) Escribe como potencias de base positiva:
17) Escribe el resultado como potencia de base positiva:
- a)
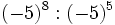 ; b)
; b) 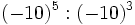
- c)
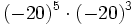 ; d)
; d) 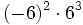
- e)
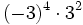 ; f)
; f) 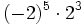
Simplifica: 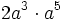
Simplifica: 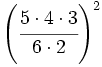
Simplifica: ![\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3](/wikipedia/images/math/7/1/b/71b5b62cb54ed835ba335fdbca4de909.png)
Simplifica: 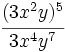
Simplifica: 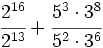
Actividades para aprender a calcular potencias de productos y cocientes.
Actividades para aprender a calcular productos y cocientes de potencias.
Actividades para aprender a calcular potencias de otra potencia.
Ejercicios resueltos sobre las propiedades de las potencias de números entero.
Actividades sobre las propiedades de las potencias de números enteros.
Ejercicios de autoevaluación sobre las propiedades de las potencias de números enteros.
Ejercicios de autoevaluación sobre las propiedades de las potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Ejercicios de autoevaluación sobre potencias de números enteros.
Raíces cuadradas de números enteros
La definición de raíz cuadrada de un número entero es la misma que la dada para números naturales.
Ver: Raíz de un número natural
La raíz cuadrada de un número  es otro número
es otro número  que elevado al cuadrado da
que elevado al cuadrado da  . Simbólicamente:
. Simbólicamente:
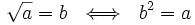
Al número  se le llama radicando y al número
se le llama radicando y al número  se le llama raíz.
se le llama raíz.
Número de soluciones de una raíz cuadrada
Dependiendo del signo del número entero, su raíz puede existir o no. Tenemos los dos casos siguientes:
Número de soluciones de la raíz cuadrada
- La raíz cuadrada de un número entero positivo tiene dos soluciones iguales pero opuestas en signo, que no siempre son números enteros.
- La raíz cuadrada de un número entero negativo no existe.
Raíz cuadrada de un número entero. Ejemplos
Simplificando raíces ccuadradas no exactas: 5\,\sqrt{117}
- Actividad para aprender a calcular raíces de números enteros.
- Actividad para practicar las raíces de números enteros.
Actividades sobre raíces cuadradas exactas y enteras.
Ejercicios de autoevaluación sobre raíces de números enteros.
Raíces cuadradas con la calculadora
|
Calculadora: Raíz cuadrada |
Raíces de otros índices (Ampliación)
Actividades sobre raíces de índice mayor que 2.
Operaciones combinadas con números enteros
A la hora de operar con números enteros utilizaremos la misma jerarquía de operaciones que con números naturales:
Ver: Jerarquía de las operaciones con números naturales
Jerarquía de las operaciones
A la hora de operar seguiremos las siguientes pautas:
- Primero se efectúan las operaciones del interior de los paréntesis. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
- Dentro de los paréntesis, o una vez quitados todos los paréntesis, las operaciones se efectúan en el siguiente orden:
- Las potencias y las raíces.
- Las multiplicaciones y las divisiones (de izquierda a derecha).
- Las sumas y las restas.
- Cuando aparecen paréntesis dentro de otros paréntesis, se puede optar por cambiar los paréntesis más exteriores por corchetes, con el fin de facilitar la lectura de la operación.
- Cuando resuelvas los paréntesis puedes completar las operaciones que encierren o aplicar la propiedad distributiva.
- En cada uno de los pasos que des para resolver una expresión con operaciones combinadas se puede llevar a cabo más de una operación, siempre que no suponga romper el orden que acabamos de establecer.
Tutorial en el que se explica a través de varios ejemplos el orden en el que hay que realizar las operaciones con números, lo que se llama la jerarquía de operaciones.
- 00:00 a 03:47 : Conceptos básicos. Jerarquía de operaciones.
- 03:47 a 19:37 : Ejercicios de Operaciones Combinadas.
Operaciones combinadas con enteros.
Efectúa:
a) 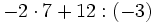
b) 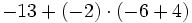
c) ![(-30):15-3 \cdot [(-3)+(-8)]\;](/wikipedia/images/math/e/6/8/e68cbfa29c5b2441d196f58e5650e229.png)
d) ![-2+4:[7+(-6):2]\;](/wikipedia/images/math/7/8/9/789c45348313c9a5a97d88770e651174.png)
e) 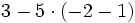
f) ![5+(-24):(+6)+5 \cdot [4-(-2) \cdot (+3)]\;](/wikipedia/images/math/3/2/e/32e813821a2ebe77944b02c2111bde3c.png)
Efectúa:
a) 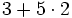
b) 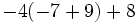
c) 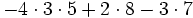
d) 
Efectúa:
a) 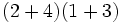
b) 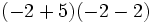
c) 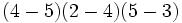
d) ![-2+[3+2(-3-1)]\;](/wikipedia/images/math/2/2/5/225a550a5c715d1274f269774c6cac8c.png)
e) ![-2{5-2[3-4+(1+2)-2(-1-1)]-3}+1\;](/wikipedia/images/math/f/1/7/f1746b8cc35742adcd78520262157f86.png)
Efectúa:
Efectúa:
a) 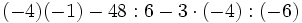
b) ![(-6):(+2)+[18-9:(+3)]\cdot (-2+4)+5 \cdot (-7)\;](/wikipedia/images/math/0/f/1/0f12794504f2a70e93d1f1a7d0f27e72.png)
Efectúa:
a) ![(-7)-\{9-[(-7)+(-13)-(-5)]+[23-(+18)+(-6)]\}\;](/wikipedia/images/math/8/5/f/85fda0cee7c9c7b7f463a471512b0756.png)
b) 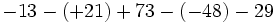
c) ![1-\{4-[-2+(5-1-9)-1]+2\}+3\;](/wikipedia/images/math/6/d/5/6d5616771a67c61c00a77f7b152ddae5.png)
Efectúa:
Efectúa:
Efectúa:
Efectúa:
Efectúa:
Efectúa:
Ejercicios resueltos de operaciones combinadas con números enteros.
En esta escena podrás practicar las operaciones con números enteros: suma, resta, multiplicación, cociente, potencia y raíz; con o sin paréntesis.
En esta escena podrás practicar las operaciones de suma, resta y multiplicación con paréntesis con 3 números enteros.
En esta escena podrás practicar las operaciones combinadas con paréntesis con 3 números enteros.
En esta escena podrás practicar las operaciones combinadas con paréntesis con 4 números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros con ayuda de la calculadora. (nivel 1)
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros con ayuda de la calculadora. (nivel 2)
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros. No incluye potencias ni raíces.
Ejercicios de autoevaluación sobre operaciones combinadas con números enteros. Incluye raíces y potencias.
Calculadora
Suma, resta, multiplicación y división
|
Calculadora: Suma, resta, multiplicación y división |
Opuesto
|
Calculadora: Opuesto |
Paréntesis
|
Calculadora: Paréntesis |
Potencias
|
Calculadora: Potencias |
Ejercicios y problemas
1) En las carreras de caballos un espectador apostó en 4 carreras y los resultados fueron estos: en la primera perdió 50 €;, en la segunda perdió 30 €; en la tercera ganó 40 € y en la cuarta ganó 600 €. ¿Cuál fue el balance total de sus apuestas?
2) La temperatura de una ciudad medida a las 7 de la mañana es de 4º sobre cero; de 7 a 10, la temperatura aumentó 5º; de 10 a 2 la temperatura aumentó 4º; de 2 a 5 no varió; de 5 a 9 descendió 3º y de 9 a 12 descendió 7º. ¿Cuál es la temperatura a las 12 de la noche?
3) A primeros de mes, Luis tenía en su cuenta 500 €. Al día siguiente ingresó 50 €. Al otro día sacó 200 € y a la semana siguiente sacó 100 €. El día 29 ingresó 250 € que le pagó un amigo. ¿Qué dinero le queda a final de mes?
4) Una sustancia que se encuentra a 50º pasa a 5º bajo cero. ¿Cuál es la variación de la temperatura?
5) La temperatura de una barra de hielo en un día de invierno es de 2º bajo cero. Se calienta y pasa a 50º sobre cero. ¿Cuál es la variación de temperatura?
6) En un juego, Luis ganó 12 cromos, después perdió 15 cromos, más tarde ganó 27 cromos y luego perdió 7 cromos. ¿Cuál fue el balance del juego?
7) Una sustancia que está a 11º bajo cero se calienta hasta ponerse a 11º sobre cero. ¿Cuál es la variación de temperatura?
8) Al construir un edificio de 10 plantas y 3 sótanos, el nivel de la calle donde está se considera altura cero; por encima, las alturas son positivas, y por debajo, negativas. calcula la distancia recorrida por un ascensor que va:
- de la altura -7 a la altura +25.
- de la altura -2 a la altura -8.
- de la altura +4 a la altura +15.
1) Una colección de libros de historia consta de 150 libros. El precio de los tres primeros juntos es de 32 euros, y el precio de los restantes hasta la mitad de la colección se vende a 25 euros cada libro. La segunda mitad de la colección se vende a 22 euros cada libro. ¿Cuál es el importe total de la colección?
2) Una isla tiene una superficie de 140 km2, y la densidad de población en esta isla (número de habitantes por km2) es de 250. La isla tiene 6 árboles por persona. ¿Cuál es el número aproximado de árboles de la isla?
3) En una bodega hay las siguientes cantidades de vino:
- 8 toneles con 10 000 litros cada uno.
- 15 toneles con 8 hl cada uno.
- 20 toneles con 6 hl cada uno.
Calcula el total de litros de vino que hay en la bodega.
Problemas de sumas y restas de enteros con o sin paréntesis.
Problemas resueltos con números enteros.
Problemas resueltos con números enteros.
Problemas resueltos con potencias y raíces de números enteros.
En esta escena podrás resolver problemas de compras en los que intervienen sumas, restas y multiplicaciones de números enteros.
|
Problemas: Operaciones con enteros
1. Estamos en la planta 345 de un gran rascacielos del futuro y bajamos en ascensor a la planta -15. ¿Cuánto tiempo tardaremos si el ascensor tarda 1 segundo en bajar 5 pisos?
Solución: 1' 12"
2. Pitágoras, filósofo y matemático griego, nació el año 582 a.C. y murió el año 496 a.C. ¿A qué edad murio? ¿Cuántos años han pasado hasta el año 2007 d.C. desde su muerte?
Solución:
3. Durante el ascenso a una montaña, la temperatura desciende 2 grados cada 200 m de ascenso. ¿A qué altura habrá que ascender para alcanzar -15ºC, si en el punto de partida, la temperatura es de 5ºC y este está a una altitud de 300 m?
Solución: 2.300 m. |

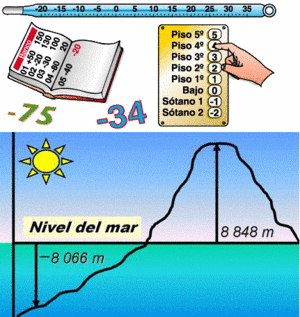

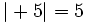
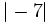
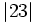
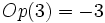 (El opuesto de 3 es -3).
(El opuesto de 3 es -3).
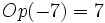 (El opuesto de -7 es 7).
(El opuesto de -7 es 7).
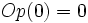 (El opuesto de 0 es 0).
(El opuesto de 0 es 0).
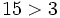
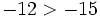
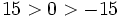
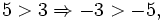
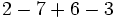
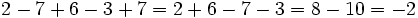
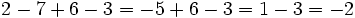
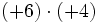
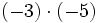
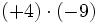
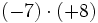
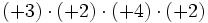
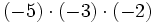
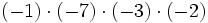
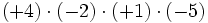
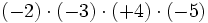
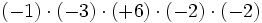
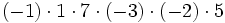
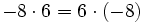
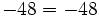
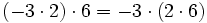
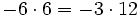
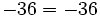
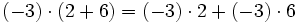
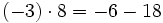
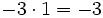
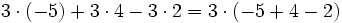
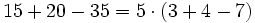
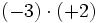
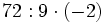
![-42 : [(-6) \cdot (-7)]\;](/wikipedia/images/math/9/7/b/97bf06a97f3e09f1e0dd13d3c5886e5a.png)
![[(+9) \cdot (-4)] : [-3 \cdot (+2)]\;](/wikipedia/images/math/0/8/5/0855f0174d3388d983075ce2f5995c46.png)
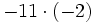
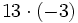
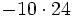
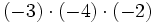

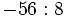
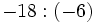
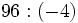
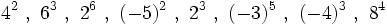
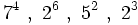

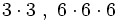
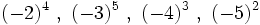
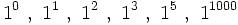
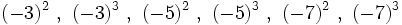
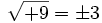
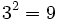
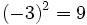
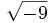 no existe, porque no hay níngún número cuyo cuadrado sea negativo, -9.
no existe, porque no hay níngún número cuyo cuadrado sea negativo, -9.
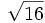
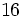
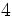
![[8-(-6)]:(+7)+(-9)\;](/wikipedia/images/math/d/7/d/d7d0b31fafbbbb0b156edb34e487cae3.png)
![18-(-2) \cdot[(+15):(8-11)]\;](/wikipedia/images/math/1/9/7/197dff4d42e5917261deea7756fe42d6.png)
![[8 + 6]:(+7)+(-9)\;](/wikipedia/images/math/8/4/e/84e6eb1dd9731dd92e13d5c09ecceff7.png)
![[14]:(+7)+(-9)\;](/wikipedia/images/math/b/8/5/b855f17314d0124a839a03b9c58ddfde.png)
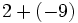
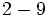
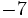
![18-(-2) \cdot[(+15):(-3)]\;](/wikipedia/images/math/b/f/f/bffdcd0011c95a2677f2441ab7af0bee.png)
![18-(-2) \cdot [-5]\;](/wikipedia/images/math/5/c/e/5cef9b8165c728c79e1c10031ec145c7.png)
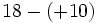
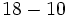
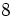
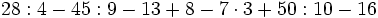
![8-\{7-[15-(6-9+1)-(3 \cdot 4-17)]\}-(-5+1)\;](/wikipedia/images/math/2/8/1/281c6dff8b881adee343ddf08db0c8ba.png)
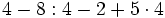
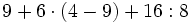
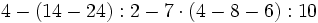
![25+40:(6-4)+[5-(8-9)]\;](/wikipedia/images/math/2/6/d/26d0311df03f52854ef572a315ff4fea.png)
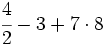


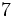
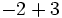
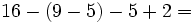
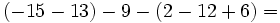
![(-3) \cdot [5 \cdot (8-6) -3 \cdot (3-7)]=](/wikipedia/images/math/f/5/9/f59deb2e37e79d7962fd952b00c1a69b.png)

